Journal tenu par Isaac Beeckman de 1604 à 1634. Tome 4: Supplément

[1629]

En visitant Beeckman, le 8^s octobre 1628, à Dordrecht, Descartes lui avait promis de lui vouloir envoyer son Algèbre après son retour à Paris (t. III, pp. 94-95). C'était sans doute de cet écrit que Beeckman tira les extraits suivants. Dans cet écrit peut avoir figuré sa propre démonstration sur l'hyperbole, qui porte en tête la date du 1^er février 1629, mais dont la proposition remonte sans doute aux entretiens d'octobre 1628, comme nous l'avons exposé lorsque nous avons reproduit ce document (t. III, p. 109). Nous attribuons cependant sans réserve une date aux environs du 1^er février 1629 aux extraits suivants, dont le premier, traitant do l'ellipse, occupe le fol. 338recto du Journal et les autres occupent fol. 339recto-340recto. Il va sans dire que les notes marginales sont de Beeckman lui-même.

Ex scriptis D. des Chartes antè saepè dicti ad verbum descripta:

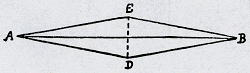
⁺Si velimus invenire superficiem in quâ omnes radij paralleli incidentes post refractionem concurrant in puncto medij densioris, ducemus ellipsim cujus maxima diameter sit ad distantiam inter utrumque focum ut sinus ingredientis anguli incidentiae ad sinum egredientis.

Verbi gratiâ, sint a et b foci ellipseos et c punctum in circumferentiâ qualecunque in quod radius hc parallelus axi refringatur: necessariò concurret cum axe in puncto a. Cùm enim major diameter^d)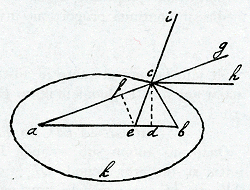



ellipseos sit ad differentiam inter focos ut α ad unitatem, linea ac juncta lineae cb erit ad ab ut α ad unitatem. Deinde divide angulum acb bifariam per lineam eci, quae secabit ellipsim ad angulos rectos; ergo ich erit angulus incidentiae radij hc, cui aequalis est ceb, cùm ch et eb sint parallelae. Cujus anguli cd est sinus rectus, si ce sit sinus totus. Eodem modo ace est angulus incidentiae in medio densiori, cujus sinus rectus est ef, ponendo iterum ce pro sinu toto. Superest igitur probandum ef esse ad cd ut unitas ad α, quod ita fit: ab est ad acb ut unitas ad α, ae est ad ac ut ab ad acb, ergo ut unitas ad α; item ef est ad cd ut ae ad ac, ergo ut unitas ad α; quod erat demonstrandum.

Estque haec foelicissima demonstratio et clarissima⁴⁾.

Ab eodem.

⁺Omnes radij ex uno puncto venientes in medio rariori et incidentes in superficiem convexam medij densioris ut fiant paralleli, oportet illam superficiem esse

+ Ellipsis in quâ omnes radij paralleli concurrent in puncto medij densioris.

d) diamer.

4) Cf. le Discours de la Mèthode (Leyde, 1637). La Dioptrique, pp. 168-170.

+ Hyperbola per quam radij in unicum punctum concurrunt.

[p. 136]

⁺ hyperbolam, in quâ distantia inter utrumque focum sit ad distantiam inter utrumque verticem, ut sinus radij ingredientis ad sinum egredientis, et focus exterior erit punctum ex quo radij omnes egredientur¹⁾.

⁺Quod si in ellipsi praecedente ex centro a circuli partem describas intra ellipsim, ita ut cbkc sit pars ellipseos, nihilominus refractio fiet in a, quia radij à centro ad circumferentiam sunt perpendiculares. Ergo comburet in a aere.

...................................²⁾

⁺Cùm D. des Chartes invenisset per parabolam duo media proportionalia inveniri³⁾, hoc mathematicus quidam Gallus Parisijs⁴⁾ geometricè demonstravit hoc modo. Quod ad verbun descripsi.

PROBLEMA SOLIDUM SOLIDE CONSTRUCTUM.

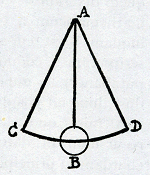
Propositis duabus lineis rectis, binas medias in continuâ proportione assignare.

Sunto binae propositae, minor GB, major BH. Oporteat autem inter eas binas medias in continuâ proportione invenire.

᾿Αναλυτικῶς

Sit jam factum et sunto in adscriptâ figurâ binae mediae, minor quidem ED, major autem EA. Quoniam igitur ED et EA sunt mediae in continuâ proportione, erit

ut GB ad ED, ita ED ad EA, et ita EA ad BH.

Quadrato autem sub secundâ DE aequatur rectangulum sub primâ et tertiâ. Igitur si statuatur secunda DE et ordinatim ducta et ad angulos rectos tertiae AE, erit AE axis parabolae cujus vertex A et latus rectum⁵⁾ erit ipsa GB prima.

Sit igitur descripta parabola. Quoniam autem

ut BG ad DE, ita DE ad EA, et ita EA ad BH,

omnibus subduplicatis (ductis nempe AD sectâ bifariam in I, et TI productâ in R, ut sit dimidio BH, hoc est BC, aequalis et parallela) erit

+ vers le 1^er février 1629

1) Cf. la démonstration de Beeckman reproduite au t. III, pp. 109-110.

+ Ellipsis pars per quam radij in aere exactè concurrunt.

2) Ici se trouve la démonstration pour l'hyperbole que nous avons reproduite au t. III, pp. 109-110.

+ Parabolâ duo media proportionalia inveniri posse demonstratur.

3) En posant a/x = x/y = y/b, le problème se ramène à la construction d'une racine de l'équation x³ = a²b, et, pour le cas spécial de la duplication du cube, à celle de l'équation x³ = 2a³. Depuis l'Antiquité on avait proposé plusieurs solutions, mais Descartes réussit à trouver une solution plus simple en ce qu'elle ne recourait qu'à une parabole et à un cercle. Cependant, dans l'été de 1625, il ne publia que la construction seule en proposant la démonstration comme un défi aux mathématiciens de Paris. Pour plus de détails cf. notre édition de la Correspondance du P. Marin Mersenne, t. I (Paris, 1932), pp. 256-259.

4) Ce mathématicien était Claude Mydorge, déjà mentionné au t. III, p. 110(n). Sur sa démonstration, valable non seulement pour le cas spécial, mais aussi pour celui où les deux lignes données seraient de longueur arbitraire, cf. pp. 269-273 de l'ouvrage cité dans la note précédente.

5) Le paramètre doublé.

[p. 137]

⁺

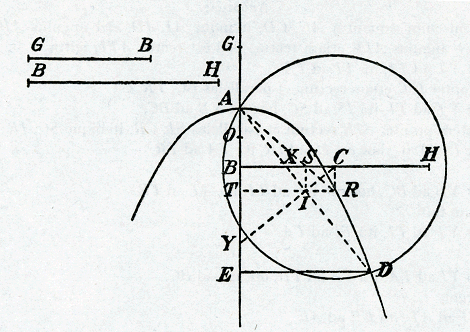ut AB ad BS, hoc est TI, ita TI ad TA, et ita TA ad TR, hoc est BC.

Sunt igitur bina ATI, ATR triangula similia et aequiangula, et angulus TAI angulo ART aequalis. Sed

ut AT ad TR, ita SI ad IR, hoc est IS ad SC (ductis nempe IS, CR axi parallelis) et ita YT ad TI.

Sunt igitur etiam similia ATR, ISR, YTI, ITA triangula et aequiangula, atque ideò anguli ART, ICS, YIT, TAI invicem aequales. Itaque propter similitudinem est

ut AT ad TI, ita TI ad TY.

Est igitur AIY angulus in semicirculo, ideòque rectus; itemque is qui deinceps AIC, etiam rectus. Igitur propter aequales AI, ID et communem IC, erunt triangula AIC, DIC invicem similia et aequalia, atque ideò AC aequalis CD et utraque radius circuli cujus centrum C.

Συνθετικῶς

Componetur igitur sic. Super ducta GE interminata secetur AB aequalis dimidio minoris extremae GB et ad rectos AB excitetur BH aequalis majori extremae; quâ bifariam sectâ in C, centro C intervallo CA describatur circuli circumferentia. Jam sectâ AB bifariam in O, foco O vertice A describatur parabola AD secans circumferentiam in D puncto à quo ad AB productam ducatur ordinatim et ad rectos DE. Dico ipsam DE esse minorem è medijs quaesitis et AE majorem. Atque sic fore

ut GB ad DE, ita DE ad AE, et ita AE ad BH.

+ vers le 1^er février 1629

[p. 138]

⁺

᾿Απόδειξις.

Quoniam enim aequantur AC, CD, itemque AI, ID, erit angulus AIC rectus atque ideò angulus AIY etiam rectus. Sed est rectus ATI, igitur

ut YT ad TI, ita TI ad TA.

Sed propter ISC etiam rectum et parallelas BC, TR, est

ut YT ad TI, ita IS ad SC, hoc est YB ad BC.

Est autem propter SIR rectum et parallelas SI, CR, itemque SC, IR

ut IS ad SC, hoc est IS ad IR, ita TA ad TR.

Igitur

ut YB ad BC, hoc est YT ad TI, ita AT ad TR.

At etiam fuit

ut YT ad TI, ita TI ad TA,

igitur

ut TI ad TA, ita TA ad TB, hoc est ad BC.

Ut autem

TI ad AT, ita DE ad AE,

et

ut AT ad TR, hoc est BC, ita AE ad BH,

igitur

ut BG ad ED, ita ED ad AE, et ita AE ad BH.

Quod erat demonstrandum¹⁾.

AUXILIO PARABOLAE OMNIA SOLIDA PROBLEMATA GENERALI METHODO CONSTRUERE.

⁺Quod alio loco vocat D. des Chartes secretum universale ad aequationes omnes tertiâ vel quartâ dimensione involutas lineis geometricis exponendas. Quod ex illius scriptis ad verbum describo:

Primò praeparetur aequatio ita ut remaneat biquadratum aequale + vel -^a) certo numero quadratorum, + vel - certo numero radicum, et + vel -^b) certo numero absoluto²⁾.

Describatur deinde parabola, cujus vertex A, focus C, ita ut latus rectum³⁾

+ vers le 1^er février 1629

1) Rappelons-y que les mathématiciens français s'occupaient dans la suite aussi de la recherche de plusieurs moyennes proportionnelles, notamment de onze, en vue de la division du manche des instruments en douze demi-tons égaux, même si ces mathématiciens rejetaient, comme Beeckman, l'égalité des tons et demi-tons.

+ Parabolâ aequationes cossicas lineis exponere.

a) minus.

b) plus vel minus.

2) C'est à dire sous la forme: x⁴ = ±ax² ± bx ± c. Pour cette équation cf. la Géométrie de Descartes (1637), pp. 383 sqq et 390 sqq.

3) Le paramètre doublé.

[p. 139]

⁺ mOn transiens per focum, sit unitas; ducaturque diameter AO utrinque in infinitum, et in illâ assumatur punctum B, vel intra vel extra parabolam, ex quo



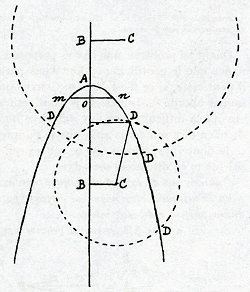ad angulos rectos educatur linea BC, et ex centro C describatur circulus DD, qui intersecabit circumferentiam parabolae in duobus^a), vel uno vel tribus^b), transeundo scilicet per verticem, vel quatuor^c) punctis, ex quibus lineae perpendiculariter descendentes supra diametrum AO erunt omnes radices propositae aequationis.

Si autem numerus quadratorum affectus sit notâ +^d), linea AB erit media pars aggregati ex unitate et numero quadratorum, assumeturque intra parabolam. Si verò affectus sit nota -^e), linea AB erit media pars differentiae inter unitatem et numerum quadratorum; atque intra parabolam, si illa differentia sit minor unitate; si verò major, erit extra; si aequalis, in vertice.

Item linea BC erit media pars numeri radicum. Et denique semidiameter circuli CD erit radix quadrata ex aggregato quadrati facti supra lineam CA et numeri absoluti, si quidem in numero absoluto fuerit nota+; si verò sit nota -, semidiameter CD erit radix differentiae, quâ quadratum lineae CA excedit numerum absolutum. Debet enim excedere: alioqui nulla est radix vera in totâ aequatione, sed omnes imaginariae, et generaliter tot tantùm sunt verae radices in aequatione, quot sunt puncta in quibus dictus circulus secat parabolam alibi quàm in vertice. Et si in numero radicum sit nota -^e), illae tantùm ex veris radicibus erunt explicitae, ex quarum extremitate lineae ductae ad centrum circuli secabunt diametrum parabolae; aliae verò sunt implicitae. Et contrà, si in numero radicum sit nota +, illae erunt radices explicitae, quae se tenent ex parte parabolae in quâ est centrum circuli; et implicitae, quaecunque in alterâ parte reperiuntur. Neque ullam planè haec regula patitur exceptionem aut defectum.

Hanc inventionem tanti facit D. des Chartes, ut fateatur se nihil unquam praestantiùs invenisse, imò a nemine unquam praestantiùs quid inventum.

+ vers le 1^er février 1629

a) 2^us.

b) 3^us.

c) 4^or.

d) plus.

e) minus.

[p. 140]

⁺

+ 28 février 1629

Le P. Marin Mersenne, à Paris, à André Rivet, à Leyde
28 février 1629

Leyde, Bibl. de l'Université, ms lat. 275, fol. 6recto-7recto. - Autographe. - Double feuillet in-fol., écrit au recto et au verso du premier, et au recto du second.

.......................................

Quant au probleme que j'avois proposé à M^sr Becman¹⁾, je n'ay point de souvenance que le gentilhomme dont vous parlez, m'en ayt satisfait et ne sçay quel il peut estre, si ce n'est M^sr De Cartes qui est le plus excellent esprit que j'aye jamais abordé²⁾. Toutesfois je vous confesse qu'il y a si longtemps que je vous envoyé la difficulté que j'ay oublié ce que c'estoit. M^sr Becman me fera plaisir de m'en dire son advis affin que je r'apprenne ce que c'est.

Je doute neantmoins que ce soit ce qui suit; et si je propose autre chose, je le prie de m'en dire aussi son advis:

Quare igitur I^o ex hypothesi quòd nervus alicujus testudinis extra lineam rectam pellatur vel adducatur usque ad certum spatium, verbi gratiâ^a) pedale, quousque in aliam partem rediturus sit³⁾?

Sit ergo nervus AB tensus ut gravior nervus testudinis alicujus. Adducatur pars



nervi et usque ad D. Si à C ad D sit pollicis spatium, aut quodvis aliud datum, quousque redibit C versus E? Hoc est: quaenam erit ratio lineae CD quae notat excursûs nervi, ad lineam CE quae notat recursûs ejusdem?

C'est ce qui ne m'a point esté solu. Le resultat de ce que j'en ay proposé audit gentilhomme n'a esté autre que ce que j'en pensois, asçavoir qu'il n'y a pas moyen de le sçavoir⁴⁾, mais parce que plus vident oculi quàm oculus, j'ay desiré sçavoir l'advis de M^r Becman⁵⁾.

Peut-estre que j'avois proposé quelqu'autre chose, mais il pourra respondre à tout ensemble.

J'ajoute que je le prie de soudre celle-cy:

Sit chorda AB quae affigatur clavo in puncto A et ex aliâ parte suspendatur ei

1) Cf. plus haut p. 133, n. 7. Quant au problème de l'ordre des consonances, Mersenne le tenait à coeur, et il l'avait proposé déjà auparavant à de divers de ses correspondants. Cf. la Correspondance du P. Marin Mersenne, t. I (1932), pp. 603 et 606-607; t. II (1936), pp. 43, 174 et 177.

2) Sur la foi de Beeckman, Rivet qui n'avait pas encore fait, à ce moment, la connaissance de Descartes, aura répondu à Mersenne que la solution de Beeckman lui devait être connu par ‘un gentilhomme’, de sa connaissance.

a) v.g.

3) Cf. t. III, pp. 185-186.

4) Cf. plus loin pp. 165, 167-168, 174 et 204.

5) En remarquant la diminution des écarts, Beeckman avait conclu à l'isochronisme des vibrationsdes cordes dans le vide; cf. t. I, pp. 249 et 259. Cf. aussi t. III, pp. 174-175 et 184-186.

[p. 141]

⁺ pondus B, quod liberè moveri queat hinc inde à B ad C et D. Si adducatur ad D, quod sit datum spatium qualecunque voluerit, quaero quousque reditura sit chorda versus C et num in omnibus recursibus



eandem rationem pondus hinc inde motum servaturus sit in singulis diminuationibus¹⁾.

Deinde ex hypothesi quòd AB faciat suum cursum à B ad D spatio unius pulsûs, quaero quanto longior debeat esse chorda ut eundem cursum faciat spatio 2 pulsuum, id est ut sit duplo quàm antea tardior.

Tertiò ex hypothesi quod pondus sit adeò parvum ut moveat chordam à B ad D spatio unius pulsûs, quaero quantum esse debeat ut duplò celeriùs illam moveat²⁾.

C'est beaucoup de peine que je vous donne, mais je ne vous prie point de cecy qu'au cas que l'execution vous en soit si facile qu'elle ne vous destourne d'aucune chose.

....................................

Je me suis adjugé et ay pris la hardiesse de rescrire à Mons^r Becman, vostre amy, auquel je mande ces difficultez plus nettement, affin que vous n'ayez point la peine de luy communiquer vostre lettre. Je vous prie de la luy faire tenir asseurement, ou de la garder jusques à ce qu'il vous vienne voir, si vous croyez qu'il doive partir avant que de pouvoir recevoir vos lettres³⁾....

+ 28 février-milieu de mars 1629

1) Cf. les études de Beeckman sur le mouvement des funépendules dans le vide, où il les croit également isochrones, t. I, pp. 254-255 et 260; sur le mouvement dans un milieu, cf. t. I, pp. 256-257. Ni Santorio, ni Mersenne semblent avoir fait quelque différence entre le mouvement dans le vide ou dans un milieu. Cf. t. III, pp. 184-186 et d'ailleurs plus loin pp. 165, 167, 174 et 204.

2) A propos du rapport entre la longueur du funépendule et le temps d'une oscillation, Santorio (cf. t. III, pp. 54 et 174) semble avoir cru que le temps est proportionnel, non aux racines, mais aux simples longueurs des fils (‘si funiculus est longior, motus pilae fit tardior et rarior; si brevior, fit frequentior et velocior’ (Comment. in primam Fen primi Libri Canonis Avicennae, Venet., 1625, Question VI, col. 21). Galilée, dans son Dialogo de 1632, semble avoir cru de même (‘Vedremo gli appesi a corde più brevi, fare lor' vibrazioni sotto più brevi tempi, come quelli che si muovono per cerchi minori’ o.c., p. 443). - Sur le même sujet cf. plus loin, pp. 164, 167, 174 et 275, n. 6.

3) Il semble qu'il faut supposer que Rivet envoya la lettre à Dordrecht.

Isaac Beeckman, à Dordrecht, au P. Marin Mersenne, à Paris.
(milieu de mars 1629)

Paris, Bibl. nat., f. fr., nouv. acq. 6206, pp. 75-78 (fol. 43recto-verso). - Autographe. - Deux feuillets in-fol. - Le texte s'arrête au milieu du verso du premier feuillet.

La date manque, mais dans les premières lignes Beeckman fait allusion à la lettre précédente de Mersenne à Rivet ou à celle que Mersenne écrivit à Beeckman lui-même 28 février. Le courier ordinaire avait besoin de huit jours pour aller d'Amsterdam (d'où il partit chaque Lundi) à Paris, mais la correspondance de Rivet et de Mersenne s'effectrait le plus souvent par voie diplomatique. D'autre part il croit Descartes encore en France; en effet celui-ci ne retourna en Hollande qu'à la fin de mars 1629 (cf. t. III, pp. 99, n. 1 et 109, n. 3). Nous datons la lettre présente donc du milieu de mars 1629.

Doctissimo viro D. Marino Marsenno mathematico insigni S.P.D. Isack Beeckman.

Non miror, Vir doctissime, virum doctum et studijs promovendis deditum, undi-

[p. 142]

⁺ que, etiam ubi nulla sunt, subsidia conquirere. Ipsissimus est D. des Chartes, quem dixeram¹⁾; cujus ingenium verè laudas quemque in Opticis tuis²⁾ nobilem mathematicum a te vocari ex multis circumstantijs certissimè colligo. Ipsus, inquam, is est, cui ante decem annos ea quae de causis dulcedinis consonantiarum scripseram³⁾, communicavi⁴⁾, quemque tibi quaestionis hujus occasionem dedisse putabam⁵⁾. Is nuper huc à vobis transivit, ac rursus (ut est peregrinandi cupidus), hinc ad vos discessit⁶⁾.

At miror quo pacto dicas te posse in nervo testudinis numerum excursuum et recursuum in dato tempore assignare, cùm practici probabiliter asseverent chordam in principio motûs acutiùs sonare quàm in fine⁷⁾; quod si mihi aperuisses, diligentiùs tuae quaestioni meritò incubuissem⁸⁾. Tunc⁹⁾, ut dixi, certò quidem demonstraveram geometricè et physicè, proportionem ictuum in chordis consonantibus eam esse quae consonantiarum; at numerum ipsum supputare, nunquam mihi in mentem venit, idque fortassis quia usum ejus rei nullum unquam vidi, nec etiam etiamnum video. Sententiam verò nunc rogatus, video in eâ re summam difficultatem, nam pendulum pondus tuum¹⁰⁾ non movetur in vacuo, sed in aere; ideòque aliter globosum, aliter pyramidale, aliter magnum, aliter parvum, aliter ligneum, aliter plumbeum movetur, quorum omnium occursus varius cum aere esset supponendus¹¹⁾. Quam ad rem tamen jam olim excogitavi modum inveniendi punctum in aere, à quo ponderis per aerem cadentis motus non ampliùs crescit, sed pondus illinc per reliquum aerem usque ad Terram aequaliter movetur¹²⁾. Ad chordae verò tuae motum et recursuum numerum, etiam aeris raritas, a Keplero forsitan non satis accuratè per refractiones supputata¹³⁾, requiritur, et nervi tenacitas totaque reflexionis natura, cujus rationem ne in laminis quidem chalibeis,

+ milieu de mars 1629

1) Cf. ci-avant pp. 133, n. 7 et 140.

2) Partie de la Synopsis mathematica que Mersenne avait publiée en 1626, et dont Beeckman avait reçu un exemplaire, de la part de Rivet (cf. t. III, p. 107). Le recueil était composé de diverses parties, parfois publiées à part, parfois réunies à diverses façons, comme le prouvent les exemplaires conservés à quelques bibliothèques. Malheureusement la partie en question n'est pas retrouvée.

3) Cf. les considérations reproduites au t. I, pp. 52-54 et ci-dessus p. 133, n. 7.

4) Cf. t. I, p. 362. Beeckman communiqua ses reflexions sur ce sujet aussi à Gassend (t. III, p. 123).

5) Outre aux occasions mentionnées ci-avant p. 171, n. 1, Descartes se trouva en France lorsque Mersenne avait proposé la question à Galilee dans sa lettre du 1^er février 1629.

6) La présence de Descartes à Amsterdam à la fin de mars 1629 est attestée par une lettre du 28 de ce mois de Reneri (cf. t. III, p. 114, n. 3) que Rivet, ayant fait tout récemment la connaissance de Descartes, avait mis en relations avec le philosophe.

7) Ayant reconnu l'isochronisme des chordes tremblantes dans le vide (cf. ci-dessus p. 140, n. 5), Beeckman n'avait pas encore étudié leur mouvement dans l'air (cf. t. III, pp. 174-175).

8) Mersenne avait constaté par expérience qu'une corde de 15 pieds tendue par un poids de 6 5/8; livres, produisait par seconde 10 tremblements, en déduisant de ce nombre celui de cordes d'autre longueur au moyen de la première partie de sa loi (cf. G. Govi, Su un'antica determinazione del numero delle vibrazioni che corrispondono a un suono della scala musicale (Rendiconti della r. Accademia delle sc. fis. e mat. di Napoli, Anno XXV (1886), pp. 106-108.

9) En même temps que le problème de la douceur des consonances. Cf. t. I, pp. 52-54.

10) Cf. ci-avant p. 141.

11) Sur l'influence de l'air cf. la remarque de Descartes plus loin p. 167.

12) Sur le point d'égalité, cf. t. I, pp. 150, 174, 263-264, 264-265, 267-268, 279, 361; t. II, pp. 244 et 330.

13) Cf. t. I, p. 99 (n).

[p. 143]

⁺ imò nec in vesicis aere plenis et à Terrâ resililientibus, satis intelligo. Nec ulla res est, super quâ doctorum sententias mathematico-physicas audire malim¹⁾.

Caeterum placet mihi haec per litteras communicatio, ideòque tibi musicâ quaestione (cùm illâ praeiveris) respondeo. Quaero cur multi psalmi alio modo a plebe canantur quàm notae indicant; non a quibusdam, sed ab omnibus; non ali <cubi>, sed ubique: non variè, sed semper eodem modo; cùm tamen, si erraret plebs, nunc ita, nunc aliter, secundùm erroris naturam, eam canentem audire conveniebat. At cùm psalmis Reformatorum non assueveris, describo tibi totum²⁾:

^a)3)

Vale, Vir doctissime, et de quâvis re, noviter ibi inventâ, me certiorem facito.

Tuus omni officio.

(au verso du second feuillet:)

Viro doctissimo

Marino Marsenno

Lutetiae Parisiorum.

+ milieu de mars-5 avril 1629

1) Sur ce sujet que Beeckman tint au coeur: t. I, pp. 40, 85, 86-87, 122, 178-179; t. II, pp. 100-101, 105, 106-107, 157, 230 et t. III, pp. 26, 127, 216, 217 et 223-224.

2) Il s'agit du Psaume 130: Du fonds de ma pensee, au fonds de tous ennuis etc.

a) L'exemple est écrit sur trois lignes, la première se terminant par la septième mesure, la seconde par la sixième mesure de notre quatrième ligne, la troisième ne reproduit que la dernière mesure.

3) Mersenne se servant de cette lettre de Beeckman, a reproduit ces diagrammes dans ses Harmonicorum Libri, t. I (Paris, 1636), Lib. VI, Prop. 24, p. 108, en les faisant précéder par ces mots: ‘Porro quaerit (Beeckman) etiam rationem cur plebs in alijs psalmis alias notas musicas corrigat, et exemplum affert ex Psalmi 130, versu 4, 5, 6 et 8, in quibus ita notae habent juxta diagrammum primum quod sequitur, et tamen plebs canit juxta diagrammum secundum’.

Le P. Marin Mersenne, à Paris, à André Rivet, à Leyde
5 avril 1629

Leyde, Bibl. de l'Université, ms lat. 275, fol. 8. - Autographe.

....................................

Je seray fort ayse de recevoir responce de M^sr Becman que vous me faites es-

[p. 144]

⁺perer¹⁾. Si par hazard vous luy rescrivez devant, et à M^sr Amama²⁾, et que le papier suffise pour leur faire mes recommandations, vous les mettrés, s'il vous plaist....

+ 5-10 avril 1629

1) Apparemment la lettre précédente, que nous croyons écrite vers le milieu de mars, hésita encore chez Rivet ou en chemin.

2) Sixten Amama, professeur d'hébreu à l'Université de Franeker, avec qui Mersenne avait également des relations.

Isaac Beeckman, à Middelbourg, à Justinus van Assche, en voyage.
10 avril 1629

Amsterdam, Bibl. de l'Eglise réformée rémontrante (cf. ci-avant p. 75). - Autographe.

Quoique la signature de l'auteur manque, celui-ci se laisse aisément reconnaître ainsi par le contenu que par l'écriture de la lettre, identique de celle du Journal.

Amantissime cognate,

En tertiam ad te a me missam epistolam: unam Leydam, alteram Emdam, ut etiam praesens. Desideramus, cùm potiùs oramus, responsum, aut si fieri possit recursum³⁾. Causam in praeteritis habuisti; in praesenti insuper accipe:

Scis te litteras a tibi notâ⁴⁾ accepisse; scis promissa tùm tua, tùm ipsius. Nosti naturam, ingenium et moras ipsius reliquaque magis tibi nota quàm exprimere possum; adde etiam illud Virgilij: Varium et mutabile semper faemina⁵⁾ tibique in alia experto crede. Ter eam hisce diebus conveni, ipsa me bis summopere responsionem desiderans de tuâ salute et animo quo adversus eam jam sic affectus, fieri certior, certè, meo judicio (quod tamen in hac re exiguum) non despectam aut neglectam oportuit. Habes animum ipsius et affectum; faxis retineas. In te jam id est ne tibi desis. Properandum ergo et festinandum quin etiam veniendum, idque quò citiùs, eò meliùs, nec expectandum ultra Kalendas Mayas ad summum. Vereor enim ne si diutiùs differas, mutato animo te deserat; optant et volunt id amici ipsius, quorum affectum in te nosti. Si verò tanta te urgeat necessitas, scribendum litterasque per avunculum⁶⁾ ad me locandas facias rogo, non meâ tantùm causâ, verùm etiam tuâ et suâ^a); jam enim res agitur et fronte capillata est post calva occasio⁷⁾.

3) Après sa résignation au ministère de Veere (cf. ci-avant p. 118, n. 2), Van Assche demeura, au début de 1628, quelque temps chez Jacob Beeckman à Rotterdam. Après son retour à Middelbourg, il se fit immatriculer à l'Université de Leyde le 11 décembre 1628. Ayant quitté cette ville, il se trouva le 10 avril 1629 à Amsterdam et reçut la lettre présente à Embden, sans doute chez son ancien collègue Fremaut (ci-avant p. 81, n. 4). Après avoir séjourné à Groningue en septembre 1629, nous le retrouvons à Middelbourg en décembre 1629.

4) Sara Beeckman, soeur de l'auteur et veuve de Jacques van Rentergem (cf. ci-avant pp. 37 et 126). Non sans difficultés, elle devint, l'année suivante, la femme de Van Assche.

5) Aeneis, Lib. IV, vs 569.

6) Abraham Arondeaux, frère de Justinus, mentionné plus haut pp. 31, 38 (n), 39 (n) et 49, Cet Abraham avait fait ses accordailles à Middelbourg, le 18 mai 1624, avec Maria Hallez, fille du médecin François Hallez. Il était marchand à Middelbourg et demeurait dans la ‘Boogaertstraete’.

a) tua et tua.

7) Cato, Dist. de Moribus, 2, 226 d'après Phèdre, Fables, 5, 8.

[p. 145]

⁺

Hisce, amantissime cognate, responsum aut recursum tuum sperante et ex intimo cordis affectu flagitante, te salutato tùm a me, tùm a tuâ, cum affine omnibusque notis. Ero semper

tuus ex animo cognatus tibi notus.

Datum Middelburgi^a), X Aprilis, quo die jam diem suum obijt pijssimus et doctissimus vir Dominus^b) Telyngius¹⁾ minister^c)2).

+ mai et juin 1629

a) middelb.

b) Dnus.

1) Willem Teeling, (sur lui t. II, p. 301 et ci-avant p. 80). Les biographes relatent sa mort au 8 avril; il fut enterré le 12 avril 1629.

c) d'abord minister diem suum obijt; puis diem suum obijt barré.

2) Van Assche a noté en marge: ‘Accepi Embdae 17^o Aprilis 1629. Respondi 22^o Apr., quas 24^o dedi. Quibus aliae fuerunt inclusae. Eodem tempore scripsi ad D^um Oostdyck (Nicolaes Oostdyck, médecin à Middelbourg) 24 Aprile et ad avunculum Abraham [Arondeaux] 24^o April. Idem ad D^um Adrianum Marievoordium Lugdunum Batavorum.

[mei 1629]

Registre des baptêmes dans l'Eglise réformée de Middelbourg, 1617-1645. - Cf. ci-avant p. 121.

Mayus 1629

....................................

16³⁾

....................................

Cornelis, f^us Johannes Everdeys ende Francyntjen de Cerff⁴⁾.

Testes: Pieter^d) Ozel⁵⁾, Isaac Beeckman ende Janneken Everdeys⁶⁾.

3) Ce nombre indique le quantième du mois.

4) Sur leur mariage cf. ci-avant p. 74. Le nouveau né mourut en bas âge.

d) P^r.

5) Sur lui cf. ci-avant pp. 34 et 74 (nn).

6) Une homonyme fut baptisée à Middelbourg le 3 août 1591 comme fille de Laurens Everdeys. Elle était la soeur de Johannes et fut enterrée à Middelbourg le 17 juin 1630.

Isaac Beeckman, à Dordrecht, au P. Marin Mersenne à Paris.
(juin 1629)

Paris, Bibl. nat., f. fr., nouv. acq. 6206; pp. 69-72 (fol. 40recto-41verso). - Autographe. - Deux feuillets in-fol., dont le recto et le verso du second feuillet sont restés en blanc.

La date manque. La première lettre de Beeckman n'était pas encore parvenue à Mersenne le 5 avril, et le second message du Minime, auquel Beeckman répond, datera donc de la fin d'avril ou du mois de mai. D'autre part la lettre doit être écrite avant la visite de Gassend à Beeckman en juillet 1629, qui n'est mentionnée que dans la lettre de Beeckman du 1^er octobre 1629. La lettre semble donc écrite vers le mois de juin 1629. Entre la réception de la présente lettre et celle du 1^er octobre Mersenne eut l'occasion d'envoyer à Dordrecht deux, au même trois, lettres.

Doctissimo mathematico D. Marino Marsenno.

Facilis tibi videtur, Vir doctissime, responsio ad quaestionem musicam a me tibi propositam⁷⁾. At ego non facilè crediderim plebem apud nos eundem ubique errorem errare, neque haec movissem nisi errorum ferè omnium in reliquis psalmis

7) Cf. ci-avant p. 143.

[p. 146]

⁺ ipse rationem reddere potuissem. Exemplo sit Psalmus 40, lineis quintâ et sextâ ad verba ‘Hors de fange et d'ordure’^a)1), ubi







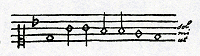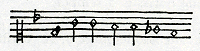^b)

Ratio est quòd e la mi debeat consonare cum g sol re ut, quia hic psalmus est secundi modi. Et fa sol, id est effa ut ad g sol re ut, hîc esse tonum minorem, probatur ex consonantijs re sol et re fa hîc frequentibus. Ablato enim re fa 6.5 à re sol 4.3, restat 10.9, quod cum 27.25 facit 6.5; distat igitur effa ut ab e la mi plus quàm semitonio²⁾. Hîc, ut tuis verbis utar, rustica natura corrigit artem³⁾.

Vide igitur annon etiam in Psalmo 130 proposito⁴⁾ indocti doctos corrigant.

Cùm dicerem⁵⁾ me rationem dulcedinis consonantiarum reddidisse, intelligebam me geometricè demonstrasse chordam, octavâ altiorem, bis recurrere eo tempore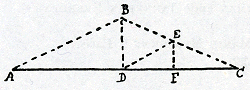



quo gravior semel. Chorda enim recta^c) AC fit AB, BC tensa et DC dimidia recta fit DE, EC tensa, etiam dimidia tensae. Sic BD duplum est EF et tempus quo B pervenit ad D, duplum ejus quo E pervenit ad F. Idem quoque de reliquis consonantijs eodem modo probabitur.

Hinc quidem sequi videtur^d) quartam dulciorem esse tertiâ majore etc. At memini me mihi hac in re ante 12 annos satisfecisse omniaque satis accuratè chartis mandasse⁶⁾, quas nunc non vacat evolvere, scholasticis negotijs nimis

+ juin 1629

a) pas de guillemets, mais des parenthèses.

1) Cf. la note du 10 septembre 1628 (t. III, pp. 80-83).

b) les figures se trouvent au milieu du texte.

2) Mersenne écrivit aussi à l'endroit cité ci-avant p. 143, n. 3: ‘Ex hac autem variâ toni majoris minorisque collatione contingit, ut cantus corrumpatur, si loco toni majoris statuatur minor et vice versa. Cujus rei exemplum mihi proposuit philosophus insignis Isaacus Beekmannus ex Psalmo 40 juxta supputationem Hebraicam, aut 39 juxta nostram, in quo plebs notas musicas Psalterij corrigit hac ratione, ut pro notis istis, quae versu quinto et sexto habentur, canat ut sequitur’. Et après avoir reproduit les deux diagrammes avec le texte suivant jusqu'au mot ‘semitonio’ inclus, il continue: ‘Ingeniosè quidem, et eâ ratione rustica natura corrigit artem. Facit enim tonum loco semitonij, sed quem tonum? Si minorem, duo toni minores sibi succederent, nempe sol, fa et fa fa, et semitonium à fa ficto ad mi semitonio majori majus esset, nempe à 27 ad 25, quod est incommodum et inusitatum; debet igitur fieri tonus major a plebe, ut duae serventur consonantiae, nempe ditonus à sol ad fa fictum, et sesquiditonus à fa ad re. Constat igitur plebem augere semitonium majus semitonio medio, quod est à 135 ad 128, ut ex semitonio majori faciat tonum majorem. Quae certè maximâ consideratione digna sunt, ne quis erret in collatione toni majoris et minoris, vel etiam semitonij in deductione modorum harmonicorum’.

3) A ce sujet cf. aussi les lettres du 1^er octobre 1629 (ci-après pp. 157 et 158) et du 30 novembre 1629 (ci-après pp. 168-169).

4) Cf. ci-avant p. 143.

5) Cf. ci-dessus p. 142.

c) recta ajouté dans l'interligne.

d) d'abord videtur quam d; puis quam d barré.

6) Cf. t. I, pp. 53-54, 191, 247-249, 250-251 et 323-324.

[p. 147]

⁺ occupato. Si tamen aliud agenti mihi in manûs aliquando incidant, statim ad te perscribam¹⁾.

Neque etiam tuis quaestionibus²⁾ incubui, cùm quia secundis litteris tuis non majorem earum usum quàm antehac aperuisti, tùm etiam quia non ostendis quo pacto observaveris chordam uno secundo temporis sexagies recurrere³⁾, ut ipse hîc potuissem idem tentare. Tubi enim duorum pedum^a) longitudine, non omnes sunt ejusdem latitudinis. Non alius igitur modus haec mihi significandi occurrit, quàm ut ipsum artificium observandi, quo manifestâ experientiâ id demonstrare te dicis, aperias.

Quae autem sit natura tensionis⁴⁾, intelliges commodissimè^b) ex instrumento Drebbeliano, quo temperies aeris exploratur. Ibi enim duplex calor aerem non reddit duplò rariorem exactè⁵⁾; in chordâ verò certum est AC tam expeditè tendi usque ad B quàm DC usque ad E, si supposueris chordam ubique esse uniformem; est enim ut AC ad DC, sic AB, BC ad DE, EC.

At hîc rationem tuam cur lamina chalybea etc. inflexa resiliat⁶⁾, iterum expecto.

Quaeris quo tempore existimem violenter mota celerrimè moveri. Respondeo lapidem projectum nunquam celeriùs moveri aut fortiùs ferire quàm cùm est in manu proijcientis⁷⁾. Idem de sagittâ dicendum. Globum verò tormentarium aliquando (non diù tamen^c)) assequitur pulvis pyrius, jam ignis factus.

Nec alia est ratio cur haec pergant moveri, quàm quia nihil impedit. In vacuo enim quo semel movetur, perpetuo eodem modo movetur. Quâ ratione nihil unquam certiùs in mentem mihi venit, nec viginti annis quicquam legi, audivi aut meditatus sum quod minimam erroris suspicionem mihi hîc movere potuerit⁸⁾.

Punctum autem, de quo tibi praecedentibus litteris scripsi⁹⁾, quodque te non intelligere dicis, invenio per bilancem¹⁰⁾. Sume igitur globum leviorem ad facilitandum experimentum, puta 12 unciarum magnitudine quàm maximum, incidatque ex alto in alteram lancem, videbis elevari uncias 13, ex altiori adhuc loco cadens elevabit uncias 14, etc., donec perveniatur ad altitudinem summam, id

+ juin 1629

1) Cf. la lettre du 1^er octobre 1629 (ci-après p. 157).

2) Cf. ci-avant pp. 140 et 142.

3) Cf. ci-avant p. 142, n. 8.

a) d'abord pedum latitu; puis latitu barré.

4) Apparemment dans les cordes. Cf. ci-après p. 159-160, 214 et 227. Mersenne a exposé, ses difficultés à propos de la tension des cordes dans son Harmonie Universelle, t. I, (1636), Livre III des Mouvemens, Prop. 14, p. 191.

b) commodisse.

5) Cf. t. II, pp. 203-204 et 361-362 et la lettre du 1^er octobre 1629 (ci-après p. 159).

6) Cf. ci-avant pp. 142-143.

7) C'était alors l'opinion générale qu'un projectile lancé a son plus grand effet au milieu de sa course. Cf. t. II, pp. 252-253 et 381 et ci-après p. 160.

c) d'abord tamen per; puis per barré.

8) On a vu que Beeckman énonce la loi d'inertie dès les notes premières de son Journal.

9) Cf. ci-avant p. 142.

10) Cf. t. I, pp. 267-268.

[p. 148]

⁺ est quâ nulla altior quicquid ponderi addit. Sit haec altitudo 100 pedum ac cadat idem globus à summitate turris cujuslibet altitudinis, videbis eum post centum pedes emensos non ampliùs celeritate crescere¹⁾.

Rationem pete ex duplicatâ proportione corporis ad superficiem²⁾. At hinc causam redde cur exigua animalia ex alto cadentia, minùs laedantur. Quo theoremate mathematico aliud nullum physico utiliùs repperi.

Sed plura fortassis jam scripsi quàm volebas, eâdem posthac brevitate, quâ praeiveris sequuturus. Salutavi tuis verbis per litteras D. des Chartes: eodem enim die, quo tuas accepi, illius etiam litterae mihi sunt redditae³⁾. Vivit, valet tibique est amicissimus.

Vale.

Dortrechti.

(au verso du second feuillet:)

Doctissimo viro

D. Marino Marsenno F.M.

à

Parys.

+ juin 1629

1) Mersenne a admis la probabilité de l'existence d'un point d'égalité dans une Proposition intitulée: ‘Asçavoir si les poids qui descendent, augmentent tousjours leur vistesse, et s'il y a quelque point d'égalité’ (Harmonie universelle, t. I (1636), Livre II des Mouvemens, Prop. 12, p. 129). C'est dans la même proposition qu'il exposa de nouveau la méthode pour mesurer une force de percussion, méthode qui fut admise aussi par des mathématiciens comme Debeaune, Gassend et Torricelli, mais critiquée par Borelli (1667) (cf., t. I, p. 268. n. 2).

2) Sur ce théorème cf. les passages cités plus haut p. 123, n. 2 et l'explication de Beeckman ci-après p. 161. Mersenne en fit mention dans ses Questions inouyes (Paris, 1634), pp. 129-130 et dans son Harmonie universelle, t. I (1636), Livre III des Mouvemens, Prop. 19, pp. 207-208.

3) Après son séjour à Amsterdam (cf. plus haut p. 142, n. 6), Descartes s'était fait immatriculer à l'Université de Franeker le 16/26 avril 1629. Sa correspondance avec Beeckman doit avoir été à cette époque assze fréquente (cf. t. III, pp. 109 et 114 et plus loin p. 196, n. 1).

René Descartes, à Franeker, à Jean Ferrier à Paris⁴⁾.
18 juin 1629.

Minute publiée par Clerselier, Lettres de M^r Descartes, où il répond à plusieurs difficultez qui luy ont esté proposées sur la Dioptrique, la Geometrie, et sur plusieurs autres sujets. Tome troisiesme et dernier. A Paris, Chez Charles Agnot, rue S. Iacques, au Lion d'Or. M.DC.LXVII. Avec privilège du Roy, p. 552.

L'auteur tache de persuader à son correspondant (avec qui il avait travaillé récemment à Paris pour la taille des verres hyperboliques) de venir chez lui et l'invite de prendre la route de Calais; et de là à Dordrecht ou à Rotterdam:

....................................

Et mesme estant à Dort, vous pourriez voir Monsieur Beecman qui est Recteur du College, et luy monstrer ma lettre. Il vous enseignera le chemin pour venir icy, et si vous aviez besoin d'argent, ou de quoy que ce soit, il vous en fourniroit, en sorte que vous ne devez conter pour la difficulté du voyage que jusqu'à Calais....

4) Pour Jean Ferrier, lunetier et artisan à Paris, cf. t. III, p. 97.

[p. 149]

⁺

+ juin et [juillet] 1629

[25 juni 1629]

Le Journal porte à fol. 234verso parmi les notes généalogiques:

Susanneken Pieters van Rhee¹⁾ is gestorven den 25^en Junij 1629, 's morgens ten 7 ueren subitelick ex catharre suffocante.

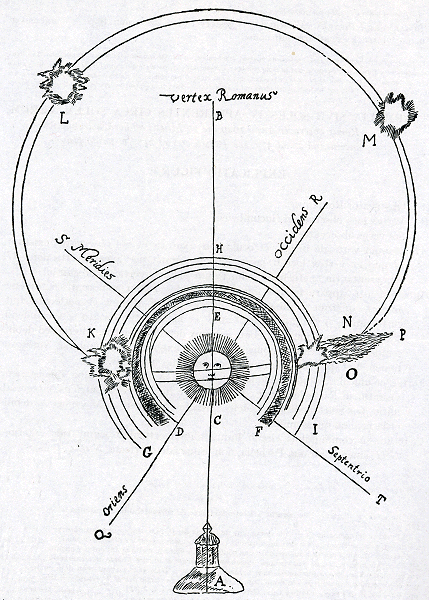
La figure suivante se trouve nu fol. 345verso du Journal, étant suivie, au fol. 346 recto et verso de son Explication. Les deux documents sont dressés par le copiste avec la main gothique. Comme il résulte du texte qui suit (cf. t. III, p. 123), Beeckman reçut ce document à l'occasion de la visite de Gassend qui avait reçu un bon nombre de copies de son mécène Peiresc à Aix en Provence²⁾ et en distribuait des exemplaires dans son voyage dans les Pays-Bas septentrionaux et meridionaux³⁾. Sur ce voyage cf. ci-après pp. 152-154.

PARHELIA SIVE SOLES IV APPARENTES CIRCA SOLEM VERUM,

Romae observati Anno 1629 die 20 Martij ab horâ astronomicâ pomeridianâ 2^a ad 3^am, seu Italicâ 20^a ad 21^am et paulò plus⁴⁾.

EXPLICATIO FIGURAE

A Observator Romanus.

B Vertex loco observatoris incumbens.

C Sol verus observatus.

AB planum verticale in quo et oculus observatoris et Sol observatus existunt, in quo et vertex loci B jacet, ideòque omnia per lineam verticalem AB. repraesentantur^a). In hanc enim totum planum verticale procumbit.

Circa Solem C apparuere duae incompletae Irides, eidem homocentricae, diversicolores, quarum^b) minor sive interior DEF plenior et perfectior fuit, curta tamen^c) sive aperta à D ad F et in perpetuo conatu sese claudendi stabat et quandoque claudebat, sed mox denuò aperiebat. Altera, sed debilis semper, et vix conspicabilis, fuit GHI, exterior et secundaria, variegata tamen^d) et ipsa suis coloribus, sed admodum instabilis.

Tertia, et unicolor, eaque valde magna Iris, fuit KLMN, tota alba, quales saepe visuntur in Paraselenis circa Lunam. Haec fuit arcus excentricus, integer ab initio, per Solis medium incedens, circa finem tamen ab M versus N debilis et lacer, imò quasi nullus.

Caeterùm in communibus circuli hujus^e) intersectionibus cum Iride exteriore GHI, emerserunt dua Parhelia, non usque adeò perfecta, N et K, quorum hoc

1) La mère de l'auteur. Elle mourut à Rotterdam âgée de soixante années; enterrée le 27 juin; cf. t. III, p. 122.

2) Peiresc lui-même avait reçu le document de la part du P. Scheiner qui avait observé le phénomène à Frascati près de Rome et il en donna plusieurs copies à Gassend pour les distribuer pendant son voyage.

3) Gassend ayant donné à Amsterdam une copie aussi à Reneri et lui ayant envoyé ensuite sa propre explication, Reneri publia le tout comme Phaenomenon rarum et illustre Romae observatum 20 Martij Anno 1629, etc. (Amstelodami, apud Hesselium Gerardi, s.d., in-4^o). Descartes ayant reçu déjà en juillet 1629 une copie manuscrite de Reneri, donna son explication dans la partie des Météores de son Discours (1637), pp. 287-294. Pour l'explication de Chr. Huygens, cf. ses Oeuvres, t. XVII (1932), pp. 381 svv.

4) Beeckman a écrit en marge: Parhelia sive Soles 4 circa Solem verum.

a) representatur.

b) quam.

c) curtatum.

d) tum.

e) huique.

[p. 150]

⁺

Les lettres B et H manquent.

+ [juillet] 1629

[p. 151]

⁺ debiliùs, illud autem fortiùs et luculentiùs splendescebat. Amborum medius nitor aemulabatur solarem, sed latera coloribus Iridis pingebantur, neque rotundi ac praecisi, sed inaequales et lacunosi, ipsorum ambitûs cernebantur. N, inquietum spectrum, ejaculabatur caudam spissam subigneam NOP cum jugi reciprocatione. L et M fuere trans zenith B, prioribus minùs vivaces, sed rotundiores et albi, instar circuli sui cui inhaerebant, lac seu argentum purum exprimentes, quamquam M mediâ tertiâ jam prope disparuerat; nec nisi exigua sui vestigia subinde praebuit, quippe et circulus ex illâ parte defecerat. Sol N defecit ante Solem K, illoque deficiente roborabatur K qui omnium ultimus disparuit.

Situm respectu plagarum mundi indicant lineae QR, ST, quarum QR aequatoris, ST meridiani cum horisonte sectionem denotat.

Sol verus, hujus phaenomeni tempore, incessit per circulos verticales qui respectu observatoris montorium, at respectu aliorum Basilicam S^ti Petri et alia loca versus castrum S^ti Angeli transeunt.

Duratio hujus apparentiae fuit, meo quidem judicio, duarum minimum horarum, nam horâ 20^a seu 2^a astronomicâ, aliqui in Collegio Romano viderunt apparentes Soles quatuor eosque satis vegetos, atque coruscos juxta Solem verum. Sed ex Tusculi in vineâ perpurgandâ occupati, quatuor a se praeter verum conspectos esse Soles valdè vegetos perscribunt, quod fieri non potuit nisi circa horam 2^am aut antè; nam post 2^am Sol M obliterari coepit, nec nisi ab hujus rei perito animadverti potuit. Ita facile mihi persuadeo hanc apparitionem duas minimum horas tenuisse et sub meridiem, vel non diù post, incaepisse, nam quando ego post horam 2^am hu[c] perveni, videbatur ad dissolutionem inclinari. In Collegio Anglicano, uti postea comperi, ex ipsismet inspectoribus nostris circa horam 19^am jam omnes Soles perfectos et fulgidos aspexerant.

Notandum insuper est circulum album KLMN ultra zenith seu verticem transivisse, prout punctum B denotat.

Tandem totam phaenomenon in nubes candidas resolutum et abstersum est circa vel paulo post horam 3^iam. Sol autem verus serenus iterum alluxit cum durante apparentiâ subobscurus, et hebes quidem, visui tamen intolerabilis affulsisset.

Sol tibi signa dabit. Solem quis dicere falsum

Audeat? ille etiam caecos instare tumultus

Saepe monet, fraudemque, et operta tumescere bella.

VIRG., I Georg.¹⁾.

OAMDG

+ [juillet] 1629

1) Vs 463-465.

[p. 152]

⁺

+ 21 juillet 1629

Pierre Gassend, à Bruxelles, à Nicolas-Claude Fabri de Peiresc, à Aix¹⁾.
21 juillet 1629

Cette lettre se trouvait autrefois à Paris, Bibl. nat., f. fr. 9536, d'où elle disparut vers 1850. Entrée dans la collection Morrison à Londres, elle fut publiée dans les Lettres de Peiresc, ed. Tamizey de Larroque, t. IV (1893), pp. 198-202, dont nous empruntons le texte suivant²⁾.

....................................

Je m'embarquay à Calais³⁾ pour la Hollande peu d'heures après que M^r De Chasteauneuf⁴⁾ fust party pour Angleterre, qui fust le deuxiesme de ce mois.

Arrivé à La Haye, M^r De Baugy, ambassadeur⁵⁾, m'y feit beaucoup de caresses.... Je pris congé de luy, fus à Leyden deux ou trois jours et y vey particulierement M^r Heinsius⁶⁾ qui me donna un exemplaire de son Laus asini augmenté⁷⁾. J'y vey aussi le bon M^r Vossius⁸⁾, qui me feit bonne chere, comme feit aussi M^r Rivet. Il seroit trop long de vous dire la peine que ces messieurs, et encores les Sieurs Heurnius⁹⁾ et Vorstius¹⁰⁾ medecins, prirent de me faire voir les eglises et tombeaux, le theatre anatomique, où il y a de tres rares choses, le jardin, etc.

A Amsterdam¹¹⁾ le Sieur Nicolaus à Wassenaer medecin qui a correspondance par tout le monde et les plus grandes raretez qu'on luy apporte de tous les endroits.... C'est luy l'autheur de ces Histoires belgiques qui s'impriment tous les six mois¹²⁾. Quand je luy eus fait voir les parhelies que vous m'aviez envoyez, il en feit faire une copie pour l'inserer dans son Histoire du semestre passé; il ne le pourra point faire sans que faisant mention de moy; il le face aussi de vous¹³⁾. Le sieur Gheritsen¹⁴⁾ qui le doit tailler, voulust que je luy tracasse un

1) Nicolas-Claude Fabri de Peiresc, né à Belgentier le 1^er décembre 1580, conseiller au Parlement d'Aix, fut l'un des plus célèbres savants de la première moitié du XVII^e siècle. Grâce à une fortune assez considérable, il pouvait se procurer une riche collection de manuscrits, de médailles et de curiosités qu'il faisait recueillir dans les pays les plus éloignés et qu'il mit à la disposition des savants. Gassend était un de ses intimes. Peiresc mourut à Aix le 24 juin 1637.

2) La collection Morrison fut dispersée de décembre 1917 à mai 1919.

3) Après avoir parcouru déjà les Pays-Bas méridionaux.

4) Charles des l'Aubespine, ambassadeur de la France en Angleterre en 1629 et 1630.

5) Nicolas de Baugy, sieur de Fay, ambassadeur de la France de 1628 à 1634.

6) Daniel Heinsius. Cf. sur lui t. II, p. 208 et ci-avant p. 76.

7) Laus asini tertiâ parte auctior. Cum alijs festivis opusculis (Lugd. Bat. ex officina Elseviriana, Anno 1629).

8) Gerard Johannis Vossius. Sur lui cf. ci-avant pp. 74 et 76.

9) Otto Heurnius, né en 1577, professeur en médecine depuis 1611.

10) Adolphe Vorstius, né à Delft en 1597, docteur de Padoue, professeur de médecine à Leyde depuis 1624 et aussi de botanique depuis 1625.

11) Gassend arriva dans cette ville vers le 8 juillet et en partit le 10 de ce mois. C'était lors de ce départ qu'il écrivit, le 10 juillet à Van Helmont à Bruxelles: ‘Si cum Dordraci fuero, repetam Caletum’ (Gassendi Opera, t. VI (1658), p. 24a).

12) Le Historisch verhael, déjà mentionné t. II, pp. 199 et 361 et dont parurent vingt-et-un volumes de 1622 à 1635.

13) Cependant, elle ne se trouve pas dans le recueil cité. Wassenaer la céda probablement à Reneri, et au libraire cité dans la note suivante.

14) Sans doute Hessel Gerritsz (± 1581-1632), célèbre graveur, cartographe et libraire, demeurant Op 't Water in de Pascaert. Il publia l'opuscule de Gassend sur les parhélies (cf. ci-dessus p. 149, n. 3).

[p. 153]

⁺ petit discours des causes de ce phenomene, pour l'adjouster à la description envoyee de Rome; je ne luy peu barbouiller que la mesme chose que je me souvenois de vous avoir escrite¹⁾. Je compris qu'il la vouloit aussi imprimer en fueille volante. Le Sieur H. Hondius²⁾ me feit veir les livres où sont des chartes de la France³⁾ et le Sieur Janssonius⁴⁾ me dit que dans peu de mois nous aurions une nouvelle spere de Copernic, en laquelle, par dessus celle que vous avez⁵⁾, il y auroit l'horizon et plusieurs autres choses⁶⁾.

A Utrecht, comme à Rotterdam, je ne trouvay point des gens de lettres de grande reputation. Ayant passé par Middelbourg en Zelande⁷⁾, je ne me souvins jamais que ce fust là la demeure du Sieur Lansbergius⁸⁾; ainsi à mon grand regret, je ne l'ay point veu.

A Dordrecht j'avoy desja veu⁹⁾, et vey despuis encore à mon retour de l'armee¹⁰⁾, le Sieur Baeckman, le meilleur philosophe que j'aye encore rencontré^a)11). A Gorckoom il y a un Maronite¹²⁾ qui a des opinions admirables touchant la disposition du Monde.

En l'armee M^r De Fresne Canaye¹³⁾, pour me faire cognoistre le Sieur Albert Girard¹⁴⁾ (celluy qui a fait r'imprimer le Marolois¹⁵⁾), ingenieur maintenant au camp, luy donna à soupper en ma compagnie. Au reste tous ces gens là sont pour le mouvement de la Terre.

Je fus au camp (vous entendez bien que c'est devant Bois le Duc¹⁶⁾) tout Di-

+ 21 juillet 1629

1) Dans une lettre inédite du 15 juin 1629 (Carpentras, Bibl. d'Inguimbert, ms 1832, fol. 15 svv. ou Paris, Bibl. nat. f. Dupuy, ms 669, fol. 177 svv).

2) Hendrick de Hondt, né en 1597, libraire et éditeur, surtout de cartes maritimes, sur le ‘Dam’.

3) Sans doute une des nombreuses éditions de l'Atlas de Mercator, récemment édité, en 1627 avec texte latin, et, en 1628, avec texte latin et français.

4) Willem Jansz (d'où Janssonius), ou Willem Jansz. Blaeu (en latin Caesius). Sur lui cf. t. II, p. 199, n. 1).

5) Sauf correction, je crois que Gassend pense à l'imitation que Peiresc avait fait faire, en 1624, du perpetuum mobile de Drebbel (cf. t. II, p. 202, n. 2).

6) Lansbergen pose la publication des sphères célestes héliocentriques de Blaeu à l'année 1628 (Bedenckingen op den dagelyckschen ende jaerlyckschen loop van den Aaerdkloot, Middelb., 1629; cf. la traduction: Commentat., Middelb., 1630, pp. 1, 15 et 51). De même Vossius, de Scientiis math., Amstelod., 1650, pp. 199-200.

7) Au début de sou voyage, venant de Calais.

8) Sur Philippe Lansbergen, cf. t. I, p. 106, n. 2; t. III, p. 225 (n) et ci-avant p. 134.

9) Probablement en passant de Rotterdam à Bois-le-Duc, le 14 juillet 1629.

10) D'après p. 154 la note 1 ce retour aurait il eu lieu le mardi 17 juillet.

a) les mots A Dordrecht et le Sieur.... rencontré soulignés, probablement par Peiresc.

11) A Dordrecht Gassend voyait d'ailleurs le médecin Jean van Beverwyck (cf. ci-après p. 228).

12) Apparemment Balthasar van der Veen. Cf. sur lui t. II, p. 388.

13) Parent sans doute de Philippe Canaye (1551-1610), auteur des Lettres et ambassades (Paris, 1645).

14) Né à Saint-Mihiel en Lorraine en 1595, ingénieur militaire dès environ 1626. En 1629 parut son Invention nouvelle en Algèbre. Il mourut à La Haye en décembre 1632; sa veuve publia sa traduction française des oeuvres de Stevin.

15) Oeuvres mathematicques, traictans de geometrie, perspective, architecture et fortification. De nouveau reveue et augmenté par Albert Girard, Amsterdam, 1628.

16) Le siège de Bois-le-Duc (mai-17 septembre 1629) par Frédéric-Henri, piqua vivement la curiosité des contemporains.

[p. 154]

⁺menche et Lundy derniers et en partis le mardy¹⁾ sur les neuf heures. J'eus le loisir et le moyen d'y voir toutes choses....

+ 21 juillet-23 août 1629

1) Le 17 juillet, lorsque Gassend vint de nouveau à Dordrecht.

Le P. Marin Mersenne, à Paris, à Isaac Beeckman, à Dordrecht.
20 août 1629

Texte incomplet du Journal, fol. 351 recto-verso.

Nous reproduisons ce texte, déjà donné au t. III, p. 134, pour mieux entendre la correspondance reproduite ici.

.... Sed et motum corporis cadentis celeriùs moveri supponis²⁾ in secundo quàm in primo, et in tertio quàm in secundo pede, quod falsum arbitror, tam experientiâ meâ quàm ratione fultus³⁾. Cur enim velociùs moveretur, cùm sit ubicunque loci et intineris ejusdem ponderis⁴⁾ et semper naturaliter descendat?⁵⁾ Immò credimus hic potius eò moveri tardiùs quò magis descendit, quamquam neque id demonstrari queat et fortasse falsum est....

2) Cf. plus haut pp. 147-148.

3) Mersenne a cru longtemps que la chute était un mouvement uniforme ou même retardé. Cf. ci-après p. 160.

4) Cette opinion résultait de diverses hypothèses par lesquelles on expliquait le phénomène de la chute des graves. Ainsi Simplicius avait supposé que le corps tombant trouvait de moins en moins d'air sous lui, tandis qu'on croyait au Moyen-âge souvent que le corps était chassé par l'air environnant. Gilbert et Galilée avaient avancé que la gravité découle de la tendance du corps de se vouloir réunir au tout (comme telle qui se manifeste dans l'action de l'aimant), ou de l'appétit qui porte le grave vers sa propre conservation. Cependant Kepler avait déjà considéré la gravité comme une qualité attractive de la Terre, soit magnétique, soit d'autre nature, Une telle attraction était déjà admise par Beeckman pendant ses entretiens avec Descartes à Breda (t. I, pp. 261-265, 267 et 279; cf. aussi ci-après p. 160 et 184).

5) Mersenne croyait alors que la pesanteur suffit pour laisser choir le corps (cf. la réponse de Beeckman ci-après p. 184). Il a discuté diverses hypothèses en cours dans son Traité des mouvemens publié en 1633; pp. 21-24; cf. notre édition de sa Correspondance, t. III (1946), pp. 630-633.

Le P. Marin Mersenne, à Paris, à André Rivet, à Leyde
23 août 1629

Leyde, Bibl. de l'Université, ms lat. 275, fol. 9 recto. - Autographe. - Une feuille in-fol., écrit au recto seul, le verso portant l'adresse.

....................................

Mons^r Gassendi⁶⁾ rescrit d'icy à Ms^r nostre ambassadeur⁷⁾, dans le paquet duquel j'ay mis celle-cy et l'autre pour Ms^r Beecman, laquelle je vous prie de luy faire tenir seurement, parce qu'elle est d'importance⁸⁾. Je croy qu'il aura receu celle que je vous envoyé par le dernier messager⁹⁾, où il y avoit un mot enfermé pour vous....

6) Gassend était rentré à Paris le 8 août 1629.

7) Nicolas de Baugy, à La Haye.

8) Lettre perdue, mais dont Beeckman nous a conservé l'extrait précédent en date du 20 août 1629.

9) Réponse sans doute à la lettre de Beeckman de juin 1629, réponse stimulée peut-être par ce que Gassend avait rapporté sur le compte de Beeckman. La lettre aurait été écrite, semble-t-il, le 17 août 1629.

[p. 155]

⁺

+ [24] août-14 septembre 1629

[augustus 1629]

Registre des baptêmes dans l'Eglise réformée de Dordrecht, 1619-1641. - Cf. ci-avant p. 127.

Augustus 1629

....................................

Par<entes>: Isaack Beeckman ende Catalyntge Cerf. 't kint Jacob¹⁾.

1) Le Journal porte à fol. 234verso, parmi les notes généalogiques:
Jacob, ons vyfde kindt, is geboren den 14^en Augusti 1629 in Dordtrecht, ten 8 ueren 's morgens, wesende Dynsdach, in de Latynsche schole.
Den 24^en Augusti is hy in de Augustinekercke van D. Everwyn (ministre à Dordrecht depuis 1626, mort en 1631) gedoopt, wesende Vrydach, op welcken dach men hier de dancksegginge dede over het veroveren van Wesel. De ghetuyghen syn: Mijnheer Cornelis van Someren (sur lui cf. t. III, p. 195, n. 3) ende D. Gosuinus Buytendyck (sur lui cf. t. III, p. 369) ende Janneken van Ryckegem, huysvrouw van myn broeder Jacob Beeckman. De getuygen in Zeelant syn: Johannes Everdeys (cf. sur lui t. II, p. 172 et ci-avant p. 74) ende Florensken de Cerf (sur elle t. I, p. 333 (n)).
Is gestorven den 4^en July 1631. Caput habebat omnino tale, medico judice, quam Hippocrates desiderat.

[27 augustus 1629]

On lit dans le Journal, à fol. 234verso, parmi les notes généalogiques:

Jacob, myn broeder²⁾, is gestorven den 27^en Augusti 1629, t'avons ten half vieren tot Rotterdam van de teeringhe. Hebbe hem doen openen ende in syn longe gevonden veel styve grauwe sweeren, gelyck kleyne Terckse boonen³⁾.

2) Jacob Beeckman, le recteur de l'école latine de Rotterdam. Lui et sa femme Janneken van Ryckegem avaient fait leur testament, le 23 août 1629, devant le notaire Adriaen Haenelaer à Rotterdam.

3) Cf. t. III, p. 444. Au moment de sa mort il laissa deux enfants: Janneken, âgée de 7½ ans (cf. ci-avant p. 74, n. 5; elle mourut à Rotterdam vers 1639) et Samuel, âgé de 3½ ans (cf. plus haut p. 95 et plus loin p. 252, n. 4). Après la mort de son mari, Janneken van Ryckegem alla probablement demeurer à Dordrecht (cf. plus loin p. 205).

Pierre Gassend, à Paris, à Isaac Beeckman, à Dordrecht.
14 septembre 1629

Texte de Petri Gassendi Diniensis Ecclesiae praepositi, et in Academia Parisiensi mathescos professoris Epistolae, quibus accesserunt clarissimorum quorundam ad ipsum epistolae et responsa. In quibus humaniorum, philosophicarum et mathematicarum rerum complura luculenter admodum enucleantur atque explicantur. Tomus sextus. Cum indicibus mecessarijs. Lugduni, sumptibus Laurentij Anisson et Ioannis Baptistae Devenet. M.DC.LVIII. Cum privilegio Regis, p. 26.

Doctissimo Viro Isaaco Beeckman Dordrechtensis Collegij Rectori Petrus Gassendus S.

Cùm nihil habeam quod ad te scribam, Beeckmane candidissime, hoc ipsum est, quod scribere placet⁴⁾. Tu, si me fortè aliquid velis, hanc in urbem rescribito; adero nempe heic hyeme totâ. Habebo brevi prae manibus meum Epicurum⁵⁾; cùm Placita viri retexam, agere aggrediar tecum de aliquibus. Nihil interea te onero cùm Mersennus noster oneret plus aequo⁶⁾.

4) A la même date, Gassend écrivit à Vossius, à Heinsius et à Golius à Leyde des lettres reproduites dans le volume cité.

5) Gassend, dont les conceptions sur la composition de la matière, sur la nature de la lumière et du son se rapprochent à celles de Beeckman, avait parlé à Beeckman et à Beverwyck, pendant sa visite à Dordrecht (cf. t. III, p. 123) des études qu'il allait entreprendre pour la réhabilitation d'Epicure. Dans une récente étude, M. Rochot attribue même à ces entretiens avec Beeckman la plus grande influence sur l'orientation de Gassend (Les travaux de Gassendi sur Epicure et sur l'atomisme (Paris, 1944), pp. VII et 36-39). On sait que les études de physique de Gassend ne furent publiés qu'à partir de 1647.

6) Mersenne avait écrit à Beeckman le 17 et le 20 août 1629 (cf. ci-dessus p. 154, n. 8 et 9). A la lettre de Gassend il ajouta un message nouveau (cf. la lettre du 1^er octobre 1629).

[p. 156]

⁺

Si Gorkomium aliquid mandes, velim illic^a) salutem dicas meo nomine et rectori illi honestissimo¹⁾ et Balthazari nostro²⁾ admirando. Quod te attinet, scito me digne sentire de tuo ingenio deque candore eximio. Scito te mihi in pectore inque medullis ipsis haerere. Scito me ad quodvis obsequium esse paratissimum.

Bene vale et bonas arteis promovere nunquam desine.

Parisijs, postridie Eidus

Septembris, Anno M.DC.XXIX.

+ 14 septembre- 1 octobre 1629

a) illi.

1) Willem Suerendonck, né le 15 janvier 1601, avait étudié en théologie à Leyde. Il devint ensuite recteur de l'école latine à Zalt-Bommel, d'où il partit en 1626 pour remplir la même fonction à Gorcum, où Adrien Heereboord, le futur Cartésien, fut un de ses élèves et où Suerendonc resta jusqu'en 1635. Cf. plus loin p. 231.

2) Balthasar van der Veen. Cf. t. II, pp. 388.

Isaac Beeckman, à Dordrecht, au P. Marin Mersenne, à Paris.
1 octobre 1629

Paris, Bibl. nat., f. fr., nouv. acq. 6206, pp. 53-58 (fol. 32recto-34verso). - De la main d'un secrétaire. - Quatre feuillets in-fol.

Doctissimo viro ac philosopho diligentissimo

D. Marino Mersenno M.

1^o Oct. 1629.

Binas à te, Vir eruditissime, accepi litteras³⁾ utrasque meis novissimis⁴⁾ respondentes.

Putas vocem humanam non exactè sequi nostros numeros⁵⁾. At si numeri hi nostri sint facti, quia dulcedo cantûs secundùm eos fieri deprehensa est, sicut ego statuo, non sequitur quidem humana vox eos numeros quia numeri sunt, sed nos discimus per numeros formas consonantiarum exprimere. Nulla enim alia ratio dari potest dulcedinis octavae quàm quia bis ferit eo tempore quo gravior ferit semel⁶⁾. Nam tempus soni gravioris^b) dividitur in duas partes aequales per unum ictuum acutioris, quae divisio tam est jucunda, ut aures^c) vix aliâ divisione delectentur. Natura ipsa nos docet identitatem esse jucundam; idcirco enim familiares, quibuscum diutiùs viximus, tam vehementer diligimus, et gratior nobis est praesentia hominis antehac visi. Sic in diapason consonantiâ idem recurrit alternis vicibus; caeteris consonantijs^d), quò rariùs ictûs coincidunt, eò sunt deteriores.

Atque hanc esse rationem cur chorda mota chordam consonantem intactam moveat⁷⁾, tuo Gassendo (cùm hîc esset) probavi⁸⁾. Non enim ob aliam causam

3) Pour ces deux lettres cf. ci-dessus p. 154, n. 8 et 9.

4) La lettre de juin 1629 (ci-avant pp. 145-148).

5) Cf. la question soulevée par Beeckman ci-avant pp. 143 et 145-146.

6) Sur le nombre des vibrations des cordes et la douceur des consonances, cf. ci-avant pp. 142 et 146.

b) d'abord gravioris bis ferit; puis bis ferit barré.

c) ut oculi.

d) consonantius.

7) Sur la résonance, cf. t. I, pp. 121, 165, 166, 244, 247 et 247-249; t. II, p. 285.

8) Dans l'été passé. Cf. t. III, p. 123.

[p. 157]

⁺ hoc fit quàm quia aer vicinus ictus movet quasvis quidem chordas. Unisonae verò ab eo ictu motae, similiter chordae tactae moventur, ideòque ictûs omnes sequentes semper motui aliquid adijciunt, dissonantes verò chordae post primum motum rarò aut nunquam similiter, id est ad easdem plagas, moventur, unde fit ut motus, per primum ictum inchoatus, per secundum etc., interrumpatur. Quae ratio D. Gassendo admodum placuit, et si diligenter meditatus fueris, genuinam esse intelliges.

In geometricâ verò proportione intervallorum musicorum, nihil nisi pythagoricum et nugatorium occurrit. Idcirco illam Stevini nostri sententiam de sex tonis continuò proportionalibus¹⁾, olim a me diligentissimè excultam, ante multos annos penitus rejeci²⁾. Practici autem ijs divisionibus utuntur quòd faciles sint et errores exigui multitudine consonantiarum occultentur³⁾. Simplex verò cantus, praeter exactam modorum et consonantiarum observationem, vix aliud habet quo tantopere delectat, cujus delectationis tu (qui hîc consonantiarum vim minuis) quam, obsecro, causam assignabis? Per aculeum enim ex priore notâ in animo relictum, mens accuratè observat consonantes notas sequentes; idcirco pro mi la sol fa semper canit fa la sol fa, etiam praevisae notae sese accommodans.

Nec de veritate axiomatis Aristotelici admodum sollicitus, qui sciam artes omnes a rusticis doceri et per rusticos probari⁴⁾. Nihil igitur plebs a peritis discit quàm id quod periti in plebe se animadvertisse existimant, et dispersa in plebe, malè interdum collegerunt. Aures quidem et vocem musicis plebs accommodat, at sibi relicta, tandem frequenti usu edocta, quod bonum est retinet, mala in bonum convertit.

Quod ad quartam attinet, quae huic rationi maximè adversari videtur, etiamsi necdum licuerit chartas meas evolvere⁵⁾, (scribam tamen quae mihi de illâ impraesentiarum occurrunt.

Constat etiam ex dictis dichotomias et combinationes naturae nostrae tam esse familiares et jucundas, ut eas, ubicunque licuerit, sponte moliatur. At quarta constat ex ratione 3 ad 4. Sive igitur gravioris chordae ictûs animo bis secentur, sive acutioris chordae ictûs combinentur, semper deterior consonantia auditur quàm representata animo^a) desideratur; representatur enim 4 ad 6 acutior, vel

+ 1 octobre 1629

1) Sur cette théorie de la gamme tempérée remontant à Aristoxene, étudiée par Vicentino, Zarlino et Salinas et défendue par Vincenzio Galilei (1580), cf. t. I, pp. 29, 88-89 et 180-181. Stevin caractérisait les intervalles exactement égaux par la proportion 12√2.

2) Probablement depuis que Beeckman avait reconnu la proportionalité inverse de la fréquence des vibrations aux longueurs des cordes (t. I, pp. 54-55; cf. t. I, pp. 88-89, 180-181, 181 et t. II, pp. 292 et 404). Descartes aussi rejetait la gamme tempérée, en général desapprouvée par ceux qui avaient l'oreille plus fine. Pour l'occupation de Mersenne avec le problème, cf. ci-après p. 180 n. 8.

3) Sur cette phrase cf. plus loin p. 180.

4) Sur cet ‘axiome’, cf. ci-avant p. 146.

5) Cf. plus haut p. 146 avec la note 6 de la même page et t. III, pp. 164-165.

a) d'abord animo auditur; puis auditur barré.

[p. 158]

⁺ 2 ad 3 gravior. Duorum autem bonorum juxta se positorum aegrè ferimus habendum esse minùs bonum, quod in tertiâ majore (4 ad 5)^a) non contingit. Nulla enim hîc est melior consonantiarum representatio nisi octavae, quae omnibus consonantijs solitarijs communis est.

Dices sextam minorem a tertiâ majore, et tertiam minorem idem pati a sextâ majore. Verùm non tanta bonitatis differentia: 12^o enim ictu quarta ter unitur, quinta quater; at 40^o ictu tertia major octies, sexta minor quinquies et 30^o ictu sexta major sexies, tertia minor quinquies. Et si octavam mente addideris, id est si ictûs acutioris chordae diviseris, habebis 2.6 | 3.8 | 4.10 | 5.12 | 3.10 | 5.18. Videbis nullam harum consonantiarum hac divisione meliores reddi praeter quintam et tertiam majorem; harum enim ictûs eo tempore quo ante mentalem divisionem semel duntaxat coincidebant, nunc bis coincidunt. Reliquae verò consonantiae ob multitudinem ictuum, nullam unionem novam representantium, potiùs obscurantur, cùmque maxima sit quintae in meliùs mutatio quàm proximè octavam representans, proportio inter hanc et quartam admodum augetur¹⁾.

Positis igitur immutabiliter consonantijs et modorum notis cardinalibus, sequitur in simplici cantu quasdam consonantias excludere in hoc vel illo modo, has vel illas notas; et hanc vel illam, hoc vel illo loco, consonantiam. Unde mihi emergunt modi modorum²⁾. Quod cùm periti non animadvertunt aequo animo pati, debent se ab imperitorum experientiâ corrigi.

Quia adhuc videre desideras quinam Psalmi hîc a nostris dicantur vulgò perperam cantari, omnes ferè enumerabo: vitia ipsa notare non vacat, multò minùs rationes eorum, inter chartas meas dispersas³⁾, colligere:

Psalmo 5, versu 2 et 3; Psal. 6, vers. 1, 4 et ultimo; Ps. 9, vers. 3; Psal. 2, vers. 4; Psal. 16, v. 5; P. 15, v. 4; P. 19, v. 3; P. 23, versu 3, 4, 5; Psalmo 27, vers. 2, 4, 5, 7, 8; P. 28, v. 3, 5; P. 33, v. 2; Psal. 36, v. 9; P. 40, v. 5 et ultimo; P. 41, v. 6; P. 46, v. 2, 4, 7, 8; Psalm. 50, v. 4 et 5; P. 66, v. 2, 6; P. 79, v. 2 et ultimo; P. 89, v. 3; Psal. 91, v. ultimo; Ps. 120, vers. 1; P. 126, v. 4, 5, 6, ultimo; P. 130, v. 2, 4, 6, ultimo; Cantico Mariae⁴⁾, v. 5; Cantico Zachariae⁴⁾, versu ultimo⁵⁾.

Quod scribis de experimento quo numerum recursuum exploras⁶⁾, vehementer placet. Usus etiam est manifestus⁷⁾.

+ 1 octobre 1629

a) pas de parenthèses.

1) Sur la douceur des consonances cf. ci-avant p. 146, n. 5 et 6; cf. aussi ci-après la lettre du 18 décembre 1629 pp. 175-176).

2) Sur ces ‘modi modorum’, cf. p. 88, 91-92, 185, 195, 269-270; t. II, p. 279; t. III, p. 68.

3) Cf. nos Tables au mot ‘Psaumes’.

4) Dans le recueil composé par Wttenhove cité au t. II, pp. 11-12.

5) Mersenne a inséré ce dénombrement également à l'endroit cité plus haut pp. 143, n. 3 et 146, n. 2. Il ajouta: ‘In quibus omnibus locis si plebs canit aliter quàm notae exprimant et bene corrigat, singularum mutationum rationes afferri poterunt, si statuantur immutabiles consonantiae et notae modorum cardinales, tuncque hae vel illae consonantiae has vel illas notas, et hanc vel illam consonantiam hoc vel illo loco excludent’.

6) Cf. plus haut pp. 140, 142 et 147.

7) Mersenne croyait pouvoir compter au moyen de ces mouvements les battements du pouls ou la durée des observations astronomiques, lors des éclipses de Soleil et de la Lune par exemple. Cf. ses Harmonic. Libri de 1636 la Prop. 27: Usum quem praedicti chordarum recursûs habere possunt etc. (p. 20) ou son Harmonie universelle, t. II (1637), Livre I des Instrumens, Prop. 19 (p. 45verso).

[p. 159]

⁺

Qualem si in reliquis quaestionibus esse ostenderis, omnem operam navabo ut eas explicem. Nunc verò dabis veniam, si ea duntaxat expediam quae mihi inter scribendum in mentem veniunt. Quae enim antè alibi^a) notavi, difficulter invenio, nec satis mihi superest temporis à reliquis negotijs de ijs quaestionibus iterum seriò meditandi.

Rogas an existimem etiam in campanis, tubis etc., recursûs esse.

Respondeo nullum sonum absque ijs fieri posse ideòque campanas, dum sonant, non tremere totas (qui tremor sonitum nullum aut exiguum saltem edit)^b), sed partes campanae vicissim introrsum et extrorsum extuberare ac sonum durare quamdiù particulae ita moventur¹⁾. Nec mirare: vitrum enim flecti potest oculis quidem, sed non alijs sensibus insensibiliter; imò in longo vitro id etiam oculis apparet. Tota haec res tibi ob oculos, aures et tactum ponitur in vitro, aquâ vel vino semipleno, cujus limbum aut pedem, si fortiter fricaveris, videbis vinum velut fervere infinitis guttulis undique exilientibus, prout unaquaeque a particulâ vitri introrsum extuberante, excutitur. Idem fieret in campanis et tubis dum sonant, si aqua in ijs contineri posset; non enim fervor iste in scypho vitreo conspicitur antequam sonitus auditur²⁾.

Aerem a duplici vi non dupliciter tendi aut comprimi³⁾, colligo^c) ex instrumento quo Hero Alexandrinus in Praefatione ad Spiritalia⁴⁾ probat in aere esse vacuum intermixtum. Si enim in fistulam tantundem secundo et tertio aquae infundas, videbis ultimâ vi aquae infusae in vase non tantum intra se cedere quàm primâ portione cedebat, quod apparet ex aquae in fistulâ hac inaequali descensu⁵⁾.

Idem de calore per candelas multiplicato concludendum est, non aliter quàm oleum aut saevum concepto mediocri calore, extenditur ac plus loci occupat; at si calorem decies multiplicaveris, non videbis molem olei magnopere augeri. Tensio autem et compressio eodem modo se habent.

Chordam nimis tensam frangi semper super circa alterutrum extremum, mihi

+ 1 octobre 1629

a) alubi.

b) pas de parenthèses.

1) Cf. t. I, pp. 53 et 192.

2) Cf. t. I, pp. 210 et 210-211. Mydorge attribuait le tremblement plutôt à la raréfaction et condensation de l'air circonfus (Examen du Livre des Recreations math., Paris, 1630, pp. 73-75). Mersenne écrivit: ‘Partium vibrationes plurimas difficultates patiuntur, cùm et ipse fremitus nondum ita descriptus esse videatur, ut quis intelligat quid sit, quibusve modis efficiatur .... Porrò similem fremitum experimur in aquâ quae bullire incipit, et in eâ quae cyatho continetur, cujus limbus digito circumducto premitur; enimverò singulae campanarum percussarum partes ita tripudiant, ut exilire et foras prorumpere videantur’ (Harmonic. Libri, t. II (1636), Lib. IV, Prop. 15, p. 161).

3) Cf. plus haut p. 147.

c) d'abord intelligo ex; puis intelligo ex barré.

4) Pour le titre de cet ouvrage, cf. t. I, p. 278.

5) Cf. les notes au t. II, pp. 203-204 et 361-362.

[p. 160]

⁺ non videtur mirum¹⁾. Ijs enim locis quibus affigitur, alterâ tantùm parte fit extensio; in medio verò hiatus utrinque compensatur. Cùmque vis ubique sit aequalis, sequitur hiatum aut poros, propè extrema, esse duplices ad poros in medio chordae.

Si nosces veram causam motûs projectorum continuati²⁾, certò scires funditores, musquetarios et pueros nucibus frangendis occupatos, falli. Hi enim prope parietem manibus tenent; idcirco tam fortiter eas non movent. Globum per pulverem pyrium emissum aliquamdiù sequitur plenitudo aeris nimia. Funditoribus contingit simile quid eo quod de pueris dixi³⁾.

Turbo postquam desijt vacillare, non movetur celeriùs, sed eidem aeri perpetuò adhaeret; hinc ille sonus. Quies verò, quam dicis, ob aliam causam introducitur, ubi etiam vera ratio reddenda cur motus turbo non cadat, et duplicis in adhuc vacillante motûs⁴⁾.

Miror autem te non credere lapidem cadentem, antequam ad punctum aequalitatis pervenerit, singulis momentis celeritate crescere⁵⁾.

Si cùm vis trahens proximo momento quidem traheret, secundo verò et tertio momentis non traheret, nemo negaverit huic lapidi per hanc vim idem contingere quod motui violento, id est pergeret moveri aliquamdiù, ut lapis projectus. At jam Terra etiam tertio et quarto momentis trahet. Primò igitur trahebat lapidem quiescentem, reliquis verò aequalium virium cum primo trahit lapidem jam in motu versus Terram existentem; ergo secundo momento movetur partim motu relicto ex primo momento, partim etiam motu novo secundi momenti et, nisi aer esset impedimento, motus lapidis cadentis cresceret usque ad centrum Terrae, ubi contingeret in quod tu dicis de eâ perforatâ⁶⁾.

+ 1 octobre 1629

1) Sur un problème analogue cf. t. II, p. 149. Mersenne avait abordé la présente question dans son Traité de l'Harmonie universelle (Paris, 1627), p. 405. Cf. aussi ci-après pp. 178 et 188.

2) Pour la loi d'inertie, cf. ci-avant p. 147.

3) Beeckman répond aux doutes de Mersenne alléguées contre la thèse émise dans la lettre précédente (p. 147). Cf. le passage de Baldi, cité et critiqué t. II, p. 381. Cf. aussi ci-après pp. 183-184.

4) Sur le mouvement d'une toupie, cf. t. I, pp. 30-32 et 242; t. II, pp. 335-337, 338 et 379; puis t. III, pp. 119 et 143.

5) Sur le point d'égalité cf. ci-dessus pp. 142, n. 12 et 147-148. Mersenne a reproduit le raisonnement de Beeckman dans un passage de son grand ouvrage que nous citons ci-après p. 171, n. 4.

6) Sur cette question de lapsu lapidis circa centrum mundi Tartaglia, Maurolic et Benedetti (Liber specul., Taurini, 1585, p. 368), avaient cru qu'un corps tombant à l'intérieur de la Terre, passerait au delà du centre, retournerait et se mouvrait ensuite autour de ce centre par des amplitudes décroissantes pour s'y mettre enfin en repos. Bacon (Novum Organum, 1620, p. 203-204) semble se rallier à cette opinion, admise aussi par Galilée (Dialogo, 1632, pp. 222-223). En effet, selon les hypothèses communes sur la gravité (cf. ci-avant p. 154, n. 4), l'accélération constante de la chute changerait seulement de signe à dans l'intérieur de la Terre à plusieurs reprises. Etant en réalité dans cet intérieur directement proportionnel à la distance du corps au centre de la Terre, ce centre devient un point asymptotique sans qu'un mouvement oscillatoire ait lieu. C'est ce que Mersenne explique sous l'hypothèse de l'attraction professée par Beeckman: ‘si le poids arrivoit jusques à la moitié du demidiametre de la Terre’-dit-il-‘toute la Terre qui est à costé de cinq cens septante-deux lieues, c'est à dire du semidiametre passé, retireroit le poids qui suit son chemin vers le centre, et la vitesse de son mouvement se diminueroit peu à peu jusques à ce qu'estant arrivé au centre, il ne pourroit plus passer outre, à raison que les deux hemispheres de la Terre le tirent pour lors également d'un costé et d'autre’ (Harmonie universelle, t. I (1636), Traitez de la nature des sons etc., Livre II des Mouvemens, Prop. 12, pp. 128-129). Cependant Mersenne garda l'ancienne conception (cf. ci-après p. 184, n. 8).

[p. 161]

⁺

Et quamquam nunquam per bilancem punctum aequalitatis exploraverim¹⁾, satis manifestò tamen hanc rem me docuit plumae et aliarum rerum in aere vel aquâ cadentium tarditas; levia enim, et parva corpora, habent magnas superficies respectu suae corporeitatis. Cùm igitur singulae particulae corporeae a Terrae centro, ut vulgò dicitur, trahantur, quò plures sunt in corpore particulae, eò fortiùs trahitur; cùmque aer superficies corporum tantum tangat quò minor est superficiei ratio ad corpus, eò minùs ab aere, qui cadendo removendus est, impeditur.

Hinc ratio petitur omnium projectorum; cur nimirum magnus globus, suppositâ virtute infinitâ, longiùs proijcitur quàm minor, gravia longiùs quàm levia; velocitatis in sagittis; proportio velorum ad naves; cur infantium ventriculus celeriùs et plura concoquat quàm adultorum; cur colossus tam diù ventis restiterit; quî vapores et fumi eleventur et infinita alia, quorum omnium ratio redditur quia corporis ad superficies ratio est duplicata. Eo planè modo quo per 19 Libri 6 Euclidis probare potest in plano urbes majores, similes et minoribus aequè frequentes, a civibus suis meliùs defendi quàm minores²⁾.

Si^a) verò tibi est animus, uti videtur, quaerendi punctum illud aequalitatis, accipe globum quàm levissimum. Et si in aere non successeris, tenta idem in aquâ, cujus corporeitas majorem quàm aer proportionem habet ad corporeitatem solidorum; quaedam enim aquis innatant, nihil verò aeri, nisi fumi forsitan et vapores³⁾.

Causa vocis auditae est idem numero aer qui erat in ore loquentis; non, ut vulgò putatur, vicissitudo sphaeralis motûs in aere, quem circulis ex projecto in aquam lapide factis assimulant⁴⁾.

Bombus verò muscae in lagenâ obturatâ auditur quia latera lagenae ab aere, per alas muscae concusso, moventur; quòque vitrum est tenuiùs, eò sincerior bombus a particulis vitri, ut antè⁵⁾ dixi, tremulis exprimitur; per ἄκαμπτα verò et densa corpora nihil bombi auditur, uti neque per nimis crassa quae a tam exiguâ vi muscae moveri nequeant. Sed cave ne ἄκαμπτα putes, quae magnâ vi incurvata quidem, non resiliunt; minore verò ictu percussa resiliunt, quale est plumbum,

+ 1 octobre 1629

1) Pour le point d'égalité et sa détermination experimentale, cf. ci-avant pp. 142, 147-148 et ci-après pp. 171, 172 (nn) et 184.

2) Sur les exemples allégués, cf. le discours inaugural de Beeckman, plus haut p. 123.

a) en marge en main de Mersenne: Punctum aequalitatis.

3) Cf. t. I, p. 265, t. II, p. 330 et plus loin p. 184 avec la note.

4) Cf. la critique de Beeckman sur l'hypothèse ondulatoire t. II, pp. 71-72. Sur la théorie d'émission qu'il admet, cf. t. I, pp. 28-29, 92-93, 252-253; t. II, pp. 232, 288, 301-302; t. III, pp. 55-56, 58-59 et 123; puis les Thèses de 1618 et plus loin pp. 177, 183, 185 et 214-215.

5) Cf. ci-dessus p. 159.

[p. 162]

⁺ etc. Sic sonus fit ex subitâ per accensum, ideòque majorem locum occupantem, pulverem pyrium aeris disjectione, eo modo quo sonus creatur in nubibus qui tonitru dicitur, ubi nullum est spiraculum simile parvulo foramini in tubo tuo bellico.

De vacuo benè argumentaris. Sive enim vacui dicantur esse pori aeris, aquae, plumbi etc., sive totus locus vacuus inter supremam circumferentiam aeris nostri et sydera, nihil absurdi sequitur. Quod enim philosophi garriunt de rerum omnium necessariâ unione¹⁾, de accidentium et specierum visibilium in aere propagatione²⁾, de impossibilitate motûs in vacuo³⁾, etc., aniles mihi videntur fabulae: nihil enim in philosophiâ admitto quàm quod imaginationi velut sensile representatur⁴⁾.

Miraris duorum lignorum gravius Sequanae vestrae innatare, levius verò innergi⁵⁾. Quod fieri nequit nisi levius poros habeat majores quibus aquam admittat, fibras verò densiores. Spongia immergitur aquae, quia^a) poros habet apertos; suber innatat aquae quia poros habet clausos.

De laminae ferreae reflectione non ampliùs urgeo⁶⁾. Quia rationes tuae conjecturis similes potiùs quàm sensiles mihi videntur, ipsemet quae aliàs⁷⁾ de hac quaestione meditatus sum, nisi tu praeoccupaveris, ad te aliquando perscribam.

De transitu in contrapuncto ab unisono ad tertiam majorem, et contrà, ipse tu tibi Libro I, theor. 21 de Musica⁸⁾ satisfecisse videris. Qui enim ab unisono ad tertiam majorem transit per tua praecepta, contra octavam duntaxat regulam peccat; qui verò transit ab eâ tertiâ ad unisonum, peccat contra 8^am et 7^am regulas simul⁹⁾. D. des Chartes, amicus noster^b), in libello suo, quem de Musicâ conscriptum ad me misit¹⁰⁾, de hac re ita scribit: ‘Ratio quare id potiùs servetur in motu a consonantijs imperfectis ad perfectas quàm in motu perfectarum ad imperfectas, est quia, dum audimus imperfectam, aures perfectiorem expectant, in quâ

+ 1 octobre 1629

1) Hypothèse entrée alors au lieu de celle de l'horror vacui pour expliquer les phénomènes du vide.

2) On se rappelle que Beeckman attribuait à la lumière une nature corpusculaire.

3) Conception, depuis Aristote, encore généralement admise.

4) Allusion à l'hypothèse de l'auteur que tout transport de force se fait par contact (matière subtile).

5) Phénomène dont Mersenne avait déjà demandé l'explication à divers correspondants.

a) les mots poros .... quia, omis par le secrétaire, sont ajoutés en marge de la main de Beeckman.

6) Cf. plus haut pp. 142-143 et 147.

7) Cf. t. I, pp. 40, 85, 85-86, 122, 178, 279; t. II, pp. 100-101, 157; puis ci-après pp. 186, 216, n. 9 et 238-239.

8) Le Traité de l'Harmonie universelle (Paris, 1627), pp. 173 sqq.

9) Depuis peu Mersenne avait posé cette question à Galilée et à Descartes, et s'informait encore dans la suite.

b) ces deux mots ajoutés par Beeckman (avec un signe d'intercalation) en marge.

10) Le Compendium Musicae, envoyé par Descartes à Beeckman le 1^er janvier 1619 et dont celui-ci avait fait faire une copie.

[p. 163]

⁺ magis quiescant, atque ad id feruntur impetu naturali. Unde fit ut magis vicina debeat poni, cùm scilicet illa sit quam desiderant; contrà verò, dum auditur perfecta, imperfectiorem nullam expectamus, ideòque non refert utra sit quae ponatur’¹⁾.

Magna certè et magnifica, imò verè philosophica sunt, quae in illis libris de Musicâ promittis²⁾, quos si quidem, ut decet, absolvas, nae tu nobis omnibus de rebus philosophicis posthac meditandi omnem ansam praeripueris.

Quae omisi talia ferè sunt, quae aut plus temporis requirunt aut minùs utilia et jucunda mihi visa aut inter legendum non animadversa sunt. Ex his, quae scripsi, satis intelligis quibus rebus delecter³⁾, et si ejusmodi quid aut ipse tu, aut Gallia tua mihi possit suggerere, gratissimum me profectò experiere.

Vale, Vir doctissime, meque D. Gassendo tuo, quando ibi alium nullum novi, commenda.

Dordrechti.

Tuus in Christo

ISACK BEECKMAN⁴⁾.

adresse:)

Viro doctissimo

D. Marino Marsenno F.M.

à

Parys.

+ 1 et 8 octobre 1629

1) Voir ce texte dans les Oeuvres de Descartes, t. X (1908), p. 133.

2) Le texte de l'ouvrage cité à la p. 162, n. 8 est précédé par un Sommaire des seize Livres de la Musique que Mersenne se proposa de composer et qui allaient constituer son Harmonie universelle (Paris, 1636 et 1637) et ses Harmonicorum Libri (ibid., 1636).

3) Cf. ci-avant p. 133.

4) Cette signature seule est autographe.

René Descartes, à (Amsterdam) au P. Marin Mersenne, à Paris
8 octobre 1629

Minute d'après l'édition des Lettres de M^r Descartes, ed. Clerselier t. II (1659), pp. 530-533. mais corrigée dans l'exemplaire de l'Institut (ms 4070), où on lit, en marge la mention: ‘ J'ay la lettre’ et la date. Les variantes de l'imprimé sont indiquies en bas des pages.

....................................

Vous m'avez extremement^a) obligé de m'advertir⁵⁾ de l'ingratitude^b) de mon amy⁶⁾. C'est, je croy^c), l'honneur que vous luy avez fait de luy escrire⁷⁾, qui l'a eblouy^d) et il a cru que vous auriez encore^e) meilleure opinion de luy, s'il vous ecrivoit qu'il a esté mon maistre il y a dix ans⁸⁾. Mais il se trompe fort, car quelle

a) extremement omis.

5) Mersenne semble avoir envoyé sa précédente lettre à Descartes vers le 14 septembre 1629 (cf. ci-avant p. 155).

b) impertinence.

6) Isaac Beeckman.

c) C'est, je crois manque.

7) Le 28 février (cf. ci-avant p. 141).

d) escrire luy a sans doute tan^t donné de vanité qu'il s'est eblouy.

e) encore omis.

8) C'est le tour que Descartes donné aux termes qu'avait employés Beeckman au début de sa lettre du milieu de mars (ci-avant p. 142).

[p. 164]

⁺ gloire y a-t-il d'avoir^a) instruit un homme qui ne sçait que tres peu de chose et^b) qui le confesse librement comme je fais? Je^c) ne luy en manderay rien, puisque vous ne le voulez pas, encore que j'eusse bien de quoy luy faire honte, principalement si j'avois sa lettre toute entiere¹⁾....

....................................

Pour l'autre question²⁾, il faudroit bien du temps pour y penser, car^d) il y a plusieurs forces differentes à considerer.

Premierement si le poids estoit en un espace vuide, où l'air ne fist aucun empeschement et qu'on supose^e) qu'il ne luy faut^f) que la moitié d'autant de temps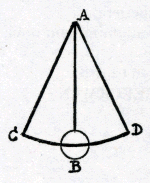



pour faire le mesme chemin lorsqu'il est poussé par une force deux fois plus grande, j'ay autresfois fait ce calcul^g). Si la corde est longue d'un pied et qu'il faille au poids un moment^h) pour passer depuis C jusques à B, la corde estantⁱ⁾ longue de 2 pieds, il luy faudra 4/3; de moment; si elle est de 4 pieds, 16/9 de moment; si de 8 pieds 64/27; si de 16 pieds 256/81^k), qui n'est guere plus de 3 momens; et ainsi des autres^l). Je ne vous dis pas pour cela combien la corde doit estre longue pour^m) que le poids emploie deux momens justement à aller de C à B, car il ne viendroit pas de nombre si facile et le calcul m'en seroit malaise à faire; mais vous voyez à proportion des autres qu'elle devroit estre plus de 5 fois plus longue³⁾.

Siⁿ⁾ bien que ce qu'elle a de moins, vient de l'empeschement de l'air, auquel il faut^o) considerer deux choses: sçavoir combien il empesche au commencement du mouvement^p) et combien par après^q). Or il faut comparer l'un et l'autre à l'augmentation de la vitesse du mouvement qui se feroit en un espace vuide, ce qui est tres difficile; et beaucoup plus en un mouvement circulaire que si vous fesiez descendre le poids en ligne droite.

Quod^r) attinet ad motûs et reditûs ponderis à C ad D, non ij minuuntur nisi

+ 8 octobre 1629

a) car il n'y a pas de gloire d'avoir.

b) sçait rien et.

c) con- fesse partout librement. Je.

1) Vers cette époque Beeckman et Descartes avaient cessé d'échanger des lettres et le dernier retira de son ancien ami l'original du Compendium Musicae qu'il lui avait donné le 1^er janvier 1619.

2) Sur le rapport entre la longueur d'un funépendule et le temps de son oscillation cf. plus haut pp. 140-141.

d) il y faudroit penser, car.

e) qu'on suposast.

f) luy fallust.

g) autresfois demonstré qu'il suivoit cette proportion; si.

h) moment seulement.

i) si la corde est.

k) et ainsi à l'infiny.

l) la figure manque.

m) pour repondre à deux momens: car elle ne se peut expliquer par 1 nombre, au moins que je croy.

3) Si Descartes ne peut pas expliquer simplement la relation entre la longueur du funépendule et la durée de son oscillation, c'est surtout parceque, pour lui, le problème est identique à celui de la chûte des graves pour laquelle il ne dispose que d'une déduction erronnée. Cf. plus loin pp. 166-167 et 173-174.

n) Et que.

o) Faut estimer deux choses differentes.

p) du mouvement omis.

q) la minute portait: et combien lorsqu'il est desja commencé à emouvoir qu'il faut encore comparer à l'augmentation de la vitesse du mouvement ce qui est tres difficile en un mouvement circulaire comme cettuycy. Il ne le serait pas du tout tant si vous supposiez que le poids descendist tout droit de haut en bas.

r) l'édition citée donne une traduction française au lieu du texte latin.

[p. 165]

⁺ a solo aere; in vacuo enim, si quid moveretur, perpetuo et eodem planè modo moveretur¹⁾.

Sed non idem est dicendum de cordâ tensâ in testudine²⁾ quae digito adducta, reddit vi sibi internâ ad priorem situm, quem etiam fortasse citiùs in vacuo recuperaret quàm in aere.

....................................

+ 8-28 octobre 1629

1) Pour la loi d'inertie, communiquée par Beeckman à Descartes dès leur premier rencontre, cf. ci-avant p. 147, n. 8 et p. 160. Sur la durée du mouvement du pendule dans la vide, Beeckman avait déjà énoncé la même opinion que Descartes, t. I, pp. 257, 259-260, 330 et t. III, pp. 174-175, 184-185.

2) Cf. t. I, pp. 249-250; t. III, p. 174 et ci-avant pp. 140-141.

[22 oktober 1629]

Résolutions du ‘Vroedschap’ de Rotterdam, Registre no 7, fol. 271. - Cf. ci-avant p.

22 October 1629

Ende also ter voorgaende vergaderingh by d'Heeren Scholarchen daerop was geinsisteert dat het t'Latynsche School alhier met een bequamen ende capabel Rector op 't spoedichste mochte werden versien³⁾, teneynde de iegenwoordiche scholieren door lange uitstel niet en werden gediverteert ende haer studie naer behooren mochten werden gevordert, hierop is verstaen dat alvooren by voorslach seker aental van personen daertoe gequalificeert, opt berd souden werden gebracht omme naer recherche ende behoorlycke informatie op derselver qualiteyten ende conditien eene uut deselviche tot het Rectorschap voorgestelt ende genomineert te werden.

Ende syn dienvolgende voorgestelt ende opt berdt gebracht dees naevolgende drie personen: Is. Beeckman, rector tot Dordrecht, A. Junius, rector te Briele⁴⁾ ende Eustathius Swartius, J.U.D.⁵⁾. Ende werden tot examinatie van partyen ende qualiteyten derselver, nevens Burgemeesteren ende Scholarchen versocht ende gecommitteert d'Heeren Hartichvelt, Sonnemans ende Lenard Busch.

3) Il résulte de la résolution précédente du 11 octobre 1629 qu'il s'agit de la vacature survenue par la mort de Jacob Beeckman.

4) Sur lui, nommé recteur de l'école latine de Brielle en juillet 1625, cf. plus haut p. 86.

5) Après eu quelque fonction dans le Palatinat, il était expulsé et demeurait actuellement à Delft.

[28 oktober 1629]

Même Registre, fol. 272.

28, October 1629.

Wyders also ter laetster vergaderingh op 't stuck van 't Rectorschap van de Latynsche schole alhier goetgevonden ende geresolveert was sekere drie personen, daertoe gequalificeert, op 't berdt te brenghen, omme daeruut, naer ernstighe recherche ende ondersouck by de Gecommitteerden hierop te doen, een ter voller vergaderingh gepresenteert ende voorgestelt te werden. Hierop is 't dat de gesamentlycke Gecommitteerden, naer behoorlycke informatie ende enqueste op de

[p. 166]

⁺ voorschreven personen gedaen ende genomen, gehoort de goede rapporten van een yder van deselve, eenstemmelyck verstaen ende geresolveert hebben de gesamentlycke drie voorgenoemde personen in vry ende vollen keure, sonder eenighe particuliere designatie, de voorschreven vergaderingh te presenteren ende voor te draghen.

Waerop eyntelyck gevolght is ende by meerderheyt van stemmen tot het voorseyde Rectorschap geeligeert de persoon van A. Junius¹⁾. Ende syn tot uutwercking van de voorsz. electie, ende omme D. Junij dimissie by de Heeren van den Briel te faciliteren, versocht ende gecommitteert d'Heeren Hertichvelt, J. Hogendorp ende P. Goederee²⁾.

+ 28 octobre et [13 novembre] 1629

1) Beeckman doit avoir renoncé à la nomination. Aussi son acte de nomination à Dordrecht (cf. ci-avant p. 120) lui interdit d'accepter un rectorat ailleurs. Cf. t. II, p. 328.

2) Cette nomination rencontra beaucoup de difficultés, le magistrat de Brielle ne voulant pas décharger Junius, Celui-ci n'entra en fonction à Rotterdam qu'au commencement de 1630; à l'automne de 1634 il fut nommé recteur à Amsterdam, où il succéda à Petrus Gruterus (cf. plus haut p. 118, n. 6).

René Descartes à (Amsterdam) au P. Marin Mersenne, à Paris.
(13 novembre 1629)

Paris, Bibl. nat., f. fr., nouv. acq. 5160, fol. 48recto et verso. - Autographe.

........................................

Pour ce que vous me demandés sur quel fondement j'ay pris le calcul du tans que le poids employe à descendre estant attaché à une chorde de 2, 4, 8 et 16 pieds³⁾, encore que je le doive mettre en ma Physique, je ne veux pas vous faire attendre jusques là, et je tascheray de l'expliquer.

Premierement je suppose que le mouvemant qui est une fois imprimé en quelque cors,



y demeure perpetuellement s'il n'en est osté par quelque autre cause, c'est à dire quod in vacuo semel incoepit moveri, semper et aequali celeritate movetur⁴⁾. Supponas ergo pondus in A existens impelli a suâ gravitate versus C, dico statim atque coepit moveri, si deseret illud^a) ipsius gravitas, nihilominus pergeret in eodem motu, donec perveniret ad C.

Sed tunc non tardiùs nec celeriùs descenderet ab A ad B quàm à B ad C. Quia verò non ita fit, sed adest illi gravitas quae premit illud^b) deorsum et addit singulis momentis novas vires ad descendendum, hinc fit ut multò celeriùs absolvat spatium BC quàm AB, quia in eo percurrendo retinet omnem impetum⁵⁾, quo movebatur per spatium AB et insuper novus ei accrescit propter gravitatem, quae de novo urget singulis momentis.

3) Cf. ci-dessus p. 164.

4) Sur la loi d'inertie, cf. ci-avant p. 165, n. 1.

a) illum.

b) premit illum.

5) Comme autrefois (cf. plus haut p. 50, n. 1). C'est au principe de la conservation de l'impetus, rejeté dar Beeckman il y avait longtemps (cf. t. I, pp. 24-25), que Descartes ramène le principe de la conservation du mouvement de Beeckman; la notion d'une attraction constante que celui-ci avait si heureusement utilisée, a disparu complètement.

[p. 167]

⁺

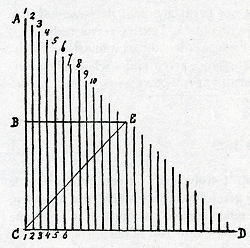
Quâ autem proportione augeatur ista celeritas, demonstratur in triangulo ABCDE. Nempe prima linea denotat vim celeritatis impressam primo momento, secunda linea^a) vim impressam secundo momento, tertia vim tertio inditam^b) et sic consequenter¹⁾. Unde fit triangulus ACD qui repraesentat augmentum celeritatis motûs in descensu ponderis ab A usque ad C; et ABE qui repraesentat augmentum celeritatis in priori mediâ parte spatij, quod pondus percurrit; et trapezium BCDE, quod representat augmentum celeritatis in posteriori mediâ parte spatij, quod pondus percurrit, nempe BC. Et cùm trapezium BCDE sit triplò majus triangulo ABE, ut patet, inde sequitur pondus triplò celerius descensurum à B ad C quàm ab A ad B; id est si tribus momentis descendit ab A ad B, unico momento descendet à B ad C, id est quattuor momentis duplò plus itineris conficiet quàm tribus²⁾, et per consequens 12 momentis duplò plus spatium quàm 9, et 16 momentis quadruplo plus quàm 9, et sic consequenter³⁾.

Quod autem de descensu ponderis per lineam rectam demonstratum est, idem sequitur de motu ponderis ad funem appensi⁴⁾, quippe in cujus motu, quantum spectat ad vim per quam movetur, non oportet consyderare arcum GH quam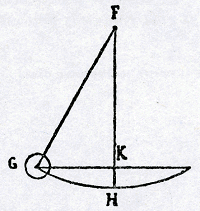



percurrit, sed sinum KH ratione cujus descendit. Ac proinde idem est ac si recta descenderet à K ad H, quantum scilicet attinet ad motum propter gravitatem.

Si verò consyderes aeris impedimentum, multò magis et aliter impedit in motu obliquo à G ad H quàm in recto à K ad H. Or pour cet empechemant de l'aer, duquel vous me demandés la justesse, je tiens qu'il est impossible d'y respondre et sub scientiam non cadit. Car s'il est chault, s'il est froid, s'il est sec, s'il est humide, s'il est clair, s'il est nebuleus, et mille autres circonstances peuvent changer l'empechemant de l'aer; et outre cela, si le poids est de plomb, de fer ou de bois, s'il est rond, s'il est quarré ou d'autre figure et mille autres choses peuvent changer cete proportion. Ce qui se peut dire generalemant de toutes les questions où vous parlés de l'empeschemant de l'aer⁵⁾.

Pour les tours et retours d'une chorde, tiree d'un poulce hors de la ligne droite⁶⁾, je dis qu'in vacuo ilz diminuent en proportion geometrique. C'est à dire si CD est 4 la premiere

+ [13 novembre 1629]

a) 1^o momento, 2^a linea.

b) 2^o momento, 3^am vim 3^am inditam.

1) En revenant à sa démonstration erronnée de 1618, Descartes se trompe de plus dans sa figure, parce qu'il tire, au lieu de parallèles à l'axe horizontal (comme il avait fait en 1618), des lignes parallèles à l'axe vertical, auxquelles il est impossible de donner une signification. Sur la démonstration actuelle de Descartes, cf. Koyré, o.c., pp. 40-45.

2) En réalité le chemin parcouru en 3 et 4 ‘moments’ est comme 3² et 4², c'est à dire comme 9 et 16, et il n'est pas ‘deux fois’ plus grand pendant le quatrième ‘moment’. Le mouvement de la chute, tel que se le représente Descartes est donc plus rapide qu'il n'est en réalité.

3) Quoique la déduction actuelle de Descartes diffère de celle qu'il avait donnée en 1618 sous l'influence de Beeckman, il arrive à la même formule fautive, formule où la vitesse est une fonction non du temps écoulé, mais de l'espace parcouru.

4) Cf. ci-avant pp. 140-141 et 164-165.

5) Cf. les considérations de Beeckman plus haut p. 142; puis plus haut pp. 123-124 et 161 et t. III, pp. 184-185, 211-212 et 239.

6) Cf. plus haut pp. 140 et 164; ci-après p. 175, n. 7.

[p. 168]

⁺ fois et au retour 2, au troisiesme il ne sera qu'un; s'il est 9 la premiere fois et 6 au second



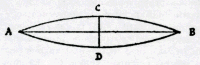coup, il sera 4 au troisiesme; et ainsy de suite. Or en suitte de cela la vistesse de son mouvement diminuera tousjours à mesme proportion, si bien qu'il luy faudra autant de tans pour chacune des dernieres allees et venues que pour les premieres¹⁾.

Je dis in vacuo, mais in aere, je croy qu'elles seront un peu plus tardives à la fin qu'au commencement, pource que le mouvement ayant moins de force, il ne surmonte pas l'empeschemant de l'aer si aysemant. Toutefois de cecy, je n'en suis pas assuré et peut-estre aussy que l'aer au contraire luy ayde à la fin pource que le mouvemant est circulaire. Mais vous le pouvés experimenter avec l'oreille en examinant si le son d'une chorde ainsy tiree, est plus aygu ou plus grave à la fin qu'au commencemant, car s'il est plus grave, c'est à dire que l'aer le retard; s'il est plus aigu, c'est que l'aer le fait mouvoir plus viste.

Et ensuitte les questions que vous me proposés combien une corde doit estre plus longue et de quel poids elle doit estre tendue affin que ces tours et retours soyent deus....²⁾.

+ 13-30 novembre 1629

1) Sur l'isochronisme des oscillations des cordes tremblantes cf. plus haut pp. 140-141 et 165.

2) La dernière feuille de la lettre fait défaut; elle traita sans doute de la question proposée plus haut pp. 140-141.

[november 1629]

Registre des baptêmes dans l'Eglise reformée de Middelbourg, 1617-1645. - Cf. ci-avant p. 121.

Novembre 1629.

....................................

18³⁾

....................................

Susanna, f^a Louwys Vergruwe ende Hester Bekemans⁴⁾.

Testes: Thomas Vergruwe⁵⁾, Isaac Bekeman, Maria Bekemans⁶⁾, Paulyntjen Aldeweerelt⁷⁾.

3) Ce nombre indique le quantième du mois.

4) Sur leur mariage, cf. plus haut p. 108.

5) Frère de Lowys; cf. sur lui plus loin p. 210.

6) Soeur d'Isaac et femme d'Abraham Janssen du Bois à Rotterdam.

7) Probablement veuve d'Anthony Alderwerelt le jeune, baptisé à Middelbourg le 8 décembre 1596 (cf. plus haut pp. 7 et 33 (n)). Elle s'était mariée à Flessingue le 26 septembre 1620 comme Paulynken Jacobs et se remaria à Flessingue en 1630.

[30 novembre 1629]

Paris, Bibl. nat., f. fr., nouv. acq. 6204, pp. 95-96 (fol. 50recto et verso). - Autographe.

Jean-Baptiste Titelouze⁸⁾, à Rouen, au P. Marin Mersenne, à Paris 30 novembre 1629

.......................................

Il y a mil autres choses à vous dire, que je reserve dans cinq sepmaines, Dieu aidant,

8) Le célèbre organiste de Rouen, né à S^t-Omer en 1563, fut nommé en 1588 organiste de la cathédrale. Il publia plusieurs pièces d'orgue (Hymnes de l'Eglise (1623), sur le Magnificat (1626), etc.). Il fut un des premiers correspondants de Mersenne et mourut en 1633.

[p. 169]

⁺ que j'espere allor à Paris. Comme aussi de cest Allemand¹⁾ qui fait un discours²⁾ pour une note que le peuple chante autrement que ne porte la note. Il y a plusieurs raisons qui seroient longues à dire et cependant c'est peu de chose que cela, car touts deux sont bons. Je dis Hors de fange et d'ordure³⁾, l'un est naturel, comme le premier; le second fait une cadence accidentelle par un b mol qui se peut faire aussi. Et les peuples septentrionaux mollisent ordinairement, et fondant et abaissant leur voix, treuvent par ce moyen plustot le b mol que nous autres qui chantons juste et ferme. Pour Ma clameur jour et nuit⁴⁾ il y a des notes changees de corde qui se sont faites ainsi par quelque ministreau qui s'en est fait acroire pour se faire valoir⁵⁾. Or pour discourir de ces petitz periodes, lesquelz sont les meilleurs, je n'ay loisir de m'estendre davantage. J'espere que nous confererons de cela à la premiere veue, encore que, comme ilz sont, il n'y ait pas grande importance au changement; mais neanmoins les differences ont des raisons diferentes aussi....

+ 30 novembre-18 décembre 1629

1) L'auteur pense aux habitants des Pays-Bas comme s'il n'y cùt rien changé depuis qu'ils furent réunis, en 1543, sous le regne de Charles, roi d'Espagne et empereur de l'Allemagne. Il s'agit bien de Beeckman.

2) Cf. ci-avant pp. 143, 145-146 et 157-158.

3) Cf. ci-avant p. 146.

4) Quatrième ligne du Psaume 130, cité par Beeckman dans sa lettre de mars 1629 (ci-avant p. 143).

5) Il s'agit probablement de Guillaume Franc, qui reçut, le 2 novembre 1552, de Theodore de Béze un certificat attestant qu'il avait été le premier auteur de la musique en usage parmi les Réformés.

[1 december 1629]

Résolutions du Vroedschap (Oud-Raad) de Dordrecht. - Cf. ci-avant p. 120.

1 Décembre 1629

Op den 1^en December 1629 geaccordeert by 't Gerecht op den voorslach van de school-versorgers, dat Dom. Abrahamus Beeckmannus, derde meester^a) in de latynsche schole tot Rotterdam, broeder van den Rector van de latynsche schole deser stede, als derde meester^a) op een provisionael tractement van tweehondert carolusguldens^b) jaerlicx tot laste deser stede, ende geleth sal werden dat in tyde ende wyle by affsterven ofte veranderinge van een van de andre meesters der voorseyde schole, egeen ander in de plaetse sal gestelt werden omme de stadt wederom van 't voorseyde tractement t'ontlasten.

a) m^r.

b) car. gl avec des traits horizontaux au dessus de ces mots.

René Descartes, à Amsterdam, au P. Marin Mersenne, à Paris.
18 décembre 1629

Paris, Bibl. de l'Institut, ms 2001, fol. 1 fol. 4; autographe. Minute aux pages 480-491 du t. II (1659), et 503-504 du t. I (1657) de l'édition de Clerselier citée plus haut p. 148.

La lettre répond à trois messages de Mersenne, dont la seconde était datée du 4 novembre et la troisième fut reçue le 17 décembre 1629.

....................................

Pour vostre façon d'examiner la bonté des consonances⁶⁾, vous m'avés appris ce que j'en devois dire; qu'elle est trop subtile, au moins si j'en ose juger, pour estre distinguee par l'oreille, sans laquelle il est impossible de juger de la bonté d'aucune consonance, et lorsque nous en jugeons par raison, cette raison doit toujours supposer la capacité de l'oreille.

6) A ce sujet cf. ci-avant pp. 142, n. 9, 146-147 et 157-158.

[p. 170]

⁺

Pour le passage de la tierce majeur à l'unison¹⁾, je me tiens à ce qu'en disent les pratticiens.

Je pense vous avoir respondu à ce que vous proposés des tours et retours d'une chorde²⁾.

....................................

Il ne reste plus que quelque chose touchant la vitesse du mouvemant que vous dite que le S^r Becman vous a mandé³⁾. Ce qui viendra mieus en respondant à vostre lettre derniere^a), in quâ 1^o petis quare dicam⁴⁾ celeritatem imprimi ut unum primo momento a gravitate et ut duo secundo^b) momento etc.

Respondeo, salvâ pace, me non ita intellexisse, sed celeritatem imprimi ut unum primo momento a gravitate, et rursus ut unum secundo^b) momento ab eâdem gravitate, etc. Unum autem 1ⁱ momenti et unum 2ⁱ faciunt duo, et unum 3ⁱⁱ faciunt tria, atque ita crescit in arithmeticâ progressione.

Hoc autem sufficienter probari putabam ex eo quòd gravitas perpetuò comitetur corpus in quo est; neque enim potest gravitas corpus comitari nisi id assiduè pellat deorsum. Nam si supponeremus, exempli causâ, plumbi massam deorsum delabentem vi gravitatis et, postquam per primum momentum labi coepit, Deum tollere omnem gravitatem ex plumbo, adeò ut postea massa plumbi non sit magis gravis quàm si esset aer aut pluma, perget nihilominus descendere ista massa, saltem in vacuo, quoniam et coepit moveri, et nulla potest afferri ratio cur desinat, sed non augebitur ejus celeritas. Atqui si post aliquod tempus restituat Deus gravitatem isti plumbo ad momentum temporis tantùm, quo elapso rursus eandem subtrahat, nunquid secundo isto momento vis gravitatis tantundem impellet plumbum quantum fecerat 1^o momento, ac proinde duplicabitur celeritas motus? Idem de reliquis momentis dicere licet⁵⁾. D'où il suit certainement que, si vous laissiés tomber une boule in spatio plane vacuo^c) de 50 pieds de hault, que de quelle^d) matiere qu'elle pust^e) estre⁶⁾, elle employeroit tousjours justement

+ 18 décembre 1629

1) Cf. ci-avant pp. 162-163.

2) Dans la lettre du 13 novembre 1629 (ci-avant pp. 167-168.

3) Cf. ci-avant p. 180.

a) A partir de ce mot, la minute de Clerselier continue par la rédaction suivante: Pour la proportion de vitesse selon laquelle descendent les pois, je vous en ay ecrit ce que j'en sçavois en la precedente, saltem in vacuo, sed in aere ce que vous a mandé Monsieur Beecman est veritable, pourvu que vous suposiez que plus le pois descend viste, plus l'air luy resiste; car si cela est, de quoy je ne suis pas encore du tout assuré, enfin il arrivera que l'air empeschera justement autant que la pesanteur adjouteroit de vitesse au mouvement in vacuo, et cela estant, le mouvement demeurera tousjours egal; mais cela ne se peut determiner que de la pensee; car en pratique il ne le faut pas esperer. Et pour vos experiences, qu'un pois, descendant de cinquante pieds, employe autant de temps à parcourir les vingt cinq derniers que les premiers, salvâ pace, je ne me sçaurois persuader qu'elles soient justes; car in vacuo, je trouve qu'il ne mettra que le tiers du temps à parcourir les vingt-cinq derniers (cf. ci-avant p. 167), et je ne puis croire que l'empeschement de l'air soit si notable qu'il rende cette difference-là imperceptible. Je suis etc. Fin du fragment Clers. I, p. 504. - Au contraire Clers.., II, p. 482 donne tout d'abord une traduction en français du passage latin (jusqu'à dicere licet).

4) Cf. ci-avant p. 167.

b) 2^o.

5) Pour le précédent cf. plus haut p. 50, n. 1, et 166-167.

c) une boule dans une espace tout a fait vuide.

d) de quelque.

e) qu'elle puisse.

6) Pour la thèse que dans le vide tous les corps tombent également vite, cf. t. II, p. 330, n. 2 et t. III, pp. 224, n. 2 et 274, n. 9.

[p. 171]

⁺ trois fois autant de tans aux 25 premiers pieds qu'elle feroit aus^a) 25 derniers¹⁾.

Mais dedans^b) l'aer c'est tout autre chose. Et pour revenir au S^r Beecman^c), encore que ce qu'il vous a mandé soit fauls, à sçavoir qu'il y ait un lieu auquel un poids^d) qui descend estant parvenu, poursuit^e) par apprès tousjours^f) d'esgale vitesse, toutefois il est vray qu'apprès certain espace cete vitesse s'augmente de si peu qu'elle^g) peut estre jugee^h) insensible. Et je m'en vois vous expliquer ce qu'il veult direⁱ⁾, car nous en avons autrefois parlé ensemble^k)2).

Supponit, ut ego³⁾, id quod semel moveri coepit, pergere suâ sponte, nisi ab aliquâ vi externâ impediatur, ac proinde in vacuo semper moveri, in aere verò ab aeris resistentiâ paulatim impediri. Supponit praeterea vim gravitatis in corpore existentem singulis momentis imaginabilibus de novo impellere corpus ut descendat, ac proinde in vacuo semper augeri celeritatem motûs eâ proportione quam supra dixi, et quam eo proponente ante undecim annos quaesivi habeoque adhuc inter mea adversaria illius temporis annotatam⁴⁾.

Addit autem de suo quae sequuntur, nempe quò celeriùs descendit aliquod corpus, tantò magis aerem ejus motui resistere⁵⁾, quod sanè hactenus mihi dubium erat, nunc autem re diligenter examinatâ, verum esse cognosco. Hinc autem sic concludit: cùm vis celeritatem faciens crescat semper aequaliter, nempe singulis momentis unitate, resistentia verò aeris celeritatem impediens, semper inaequaliter, nempe primo^l) momento sit quidem minor unitate, sed aliquantulum augeatur secundo momento et sequentibus, necessariò, inquit, eo usque perveniet ut ista resistentia sit aequalis impulsui gravitatis, tantumque detrahat ex celeritate quantum vis gravitatis adjungit. Eo autem momento quo id contingit, certum est, inquit, pondus celerius non descendere quàm momento proxime praecedenti; sed neque sequentibus momentis celeriùs augebitur vel minuetur, quia deinceps aeris resistentia manet aequalis - ejus enim inaequalitas veniebat ab inaequalitate

+ 18 décembre 1629

a) austant de tans à descendre les vingt-cinq premiers pieds que les.

1) Sur ce résultat faux, cf. ci-avant p. 167. Descartes le croyait juste encore plusieurs années après.

b) Mais dans.

c) au S^r N.

d) une pierre.

e) parvenue, elle descendra.

f) tousjours omis.

g) vray que cette augmentation de vitesse est si petite après certain espace qu'elle.

h) estimee.

i) faut dire.

k) ensemble et je vous diray après en quoy il se meprend.

2) Cf. t. I, p. 361.

3) En réalité c'était Beeckman qui avait communiqué à Descartes le principe d'inertie. Cf. plus haut p. 165 (n) et les notes de Descartes lui-même, t. I, pp. 360-361.

4) Pour les hypothèses auxquelles Beeckman assujetta la solution de son problème, cf. t. I, pp. 263 et 360-361, et quant à la dernière, cf. t. I, pp. 44, 174 et 261; cf. t. II, p. 243. Mersenne, en gardant le faux résultat de Descartes, a reproduit l'hypothèse de Beeckman, énoncée ci-avant p. 160, dans les termes suivants: ‘Je sçay qu'un excellent philosophe s'est imaginé que le poids pressant perpetuellement l'air, augmente tousjours sa vistesse, de sorte que si après le premier moment, auquel la pierre se meut, Dieu luy ostoit sa pesanteur, elle descendroit encore par la force du mouvement qu'elle s'est imprimee au premier moment, et que si elle estoit dans le vuide, elle iroit toujours d'une esgale vitesse; mais parce que la pesanteur accompagne tousjours le premier mouvement, elle accroist sa vitesse d'un degré à chaque moment, d'où il s'ensuit que la pierre ne fait pas plus de chemin aux trois premiers momens qu'au quatriesme’ (Harmonie universelle, t. I (Paris, 1636), Livre III des Mouvemens et du son des chordes, Prop. 19, p. 206).

5) Cf. t. I, pp. 233, 254, 263-264 et t. II, pp. 244, 299-300, 434, 434-435.

l) 1^o momento.

[p. 172]

⁺ celeritatis quae sublata est - vis autem gravitatis semper aequaliter pellit^a).

Il y a grande apparence en cete raison, et il la pourroit persuader à ceus qui ne sçauroint pas l'Arithmetique, mais il ne fault que sçavoir compter pour trouver qu'elle est faulse. Car si la resistance de l'aer s'accroist à mesure que la force de la vitesse s'accroist, elle ne ce peut donc accroistre plus que cete vitesse s'accroistra, c'est à dire que suivant la mesme proportion¹⁾. Faisons donc qu'au^b) commencemant du mouvemant la vitesse seroit un^c), si l'aer n'empeschoit point, mais qu'elle n'est qu'un demi; c'est donc à dire que la resistence de l'aer est aussy ½. Or, au second momant^d) que la pesanteur adjouste encore une unité à la vitesse, elle seroit de 3/2 si l'aer n'empeschoit derechef; mais de combien empeschera-t-il? On peut bien dire que ce ne sera pas tant à proportion que la premiere fois, à cause qu'il est desia esmeu, et en ce cas la proposition dudit S^r sera d'autant moins veritable. Mais on ne peut pas dire qu'il empesche plus qu'à mesme proportion que la premiere fois, c'est à dire qu'il diminuera la moitié de la vitesse, qui de 3/2 ne sera que ¾. Et au troisiesme momant la pesanteur y adjoustera encore une unité à la vitesse, qui seroit 7/4 sans que l'aer en oste la moitié et reste ⅞. Et ainsi de suitte aus autres momans l'empeschemant de l'aer sera 15/16, 31/32, 63/64, 127/128, 255/256 et sic in infinitum, où vous voyés que ces nombres croissent tousjours et toutefois sont toujours moindres que l'unité²⁾. Ac proinde nunquam tantum detrahitur de celeritate per resistentiam aeris quantum ei accrescit per gravitatem, quae nempe, singulis momentis illam auget unitate. Hoc fiet eodem modo si dicas aeris resistentiam tollere ⅔ vel ¾ celeritatis etc. Non autem potes dicere eam primo momento^e) tollere unitatem celeritatis; ita enim pondus non descenderet^f).

+ 18 décembre 1629

a) tout le passage latin qui précède est donné dans l'édition citée en français.

1) En continuant l'exposé cité ci-dessus p. 171, n. 4, Mersenne a reproduit la théorie de Beeckman dans les termes suivants: ‘Cecy posé, il conclud qu'elle rencontre un certain point d'esgalité, depuis lequel elle descend tousjours de mesme vitesse. Ce qu'il prouve parce que l'air qui resiste tousjours de plus en plus à proportion qu'il est plus violente, ne resiste pas tant au premier moment que la vitesse est augmentee comme il fait après. Par exemple la vitesse s'augmente d'un degré à chaque moment et la resistance de l'air ne croist pas d'un degré, mais parce que sa resistance croist tousjours, elle devient enfin si grande qu'elle est esgale à l'impulsion ou à la force de la pesanteur et par consequent elle empesche tousjours d'oresnavant que la pesanteur n'adjouste un degré de vitesse à chaque moment, de sorte que le mouvement demeure esgal’ (Harmonie universelle, t. I, 1636), Livre III, Prop. 19, p. 206).

b) s'accroist, ce ne peut donc estre tout au plus qu'en proportion geometrique, c'est à dire si au.

c) est un, l'air n'empeschant point et qu'elle soit seulement un demy, à cause que l'air empesche, on dira que.

d) est la moitié d'autant que la vitesse. Et au. - à partir de ce mot la minute porta: que la vitesse accroist d'une unité et par consequent seroit de 3/2 sans le second empeschement de l'air lequel on peut bien supposer n'estre pas si grand à proportion que le premier, mais non pas estre plus que la moitié de la vitesse, et lequel sera maintenant ¾. Si on dit qu'il soit moindre, il arrivera dautant moins à ce qu'on cherche. D'estre plus grand que la moitié de la vitesse, il est impossible d'en imaginer de raison. Posons donc qu'il soit egal, c'est à dire de ¾ au second moment, au troisiesme par consequent il fera de ⅞ et au quatrieme de 15/16 etc., et ainsy à l'infiny, où vous.

2) Beeckman ne paraît pas s'être prononcé exactement sur le rapport entre la vitesse du mobile et la resistance qu'il éprouve (cf. t. I, p. 263), mais il croyait bientôt après cette résistance proportionnelle au carré de la vitesse Chr. Huygens avait mis d'abord la résistance simplement proportionnelle à la vitesse du mobile (Discours de la cause de la pesanteur (1690), p. 169). C'est a que fit aussi Newton dans ses Principia de 1687.

e) 1^o momento.

f) Passage traduit en français, et suivi de la longue addition suivante: Et mesme il n'y a personne qui ne sçache qu'une quantité peut estre accruë à l'infiny sans qu'elle puisse jamais devenir egale à une autre, qui toutesfois ne s'aug- mentera point. Par exemple si vous adjoustez à l'unité un demy et puis ¼, et puis ⅛, et ainsi tousjours la moitié de ce que vous y aviez adjouté la derniere fois, vous pourrez augmenter cette unité à l'infiny sans toutesfois qu'elle soit jamais egale au nombre de deux. Or il faut necessairement qu'il avoue que c'est en cette proportion que l'air resiste, à sçavoir en proportion geometrique avec la vitesse du mouvement. Car si c'est cette vitesse qui est cause de cette augmentation de resistance de l'air, il faut necessairement qu'à proportion que la vitesse croistra, la resistance de l'air croisse aussi, et non pas ny plus ny moins. Posons donc qu'une boule descende dans l'air, et que la force de la pesanteur la pousse au premier moment comme un, la vitesse seroit aussi alors comme un dans le vuide; mais posons que la resistance de l'air oste tousjours, comme je viens de dire, la moitié de la vitesse, il s'ensuit que la vitesse de la descente ne sera pas comme un demy au premier moment; mais au second moment la pesanteur pousse derechef le corps grave comme un, et partant au second moment la vitesse seroit comme 3/2 ou 6/4, si l'air n'aportoit point de resistance. Mais pource que la resistance qu'il apporte en oste encore la moitié, la vitesse ne sera que de ¾ au second moment, et au troisiesme de ⅞, au quatriesme de 15/16, et ainsi à l'infiny. Et partant la vitesse sera tousjours augmentee; et jamais comme j'ay dit, la resistance de l'air de diminuera d'autant la vitesse, qu'elle reçoit d'accroissement par la pesanteur; à cause que ce qui est ainsi osté, n'ega- lera jamais l'unité que la pesanteur luy donne à tous les momens.

[p. 173]

⁺

Ac proinde mathematicè demonstratur illud quod Becmannus scripserat, esse falsum¹⁾. Et si vous luy escrivés, je ne seray pas^a) marry que vous lui mandiés^b), affin qu'il apprene à ne se glorifier pas mal à propos des plumes d'autruy²⁾.

Mais^c) pour revenir au poids qui descend, on peut voir par ce calcul que l'inesgalité de la vitesse^d) est tres grande au commancemant du mouvement, mais qu'elle est presque insensible^e) par apprès, et de plus qu'elle se rend plus tost insensible en un poids de matiere legere qu'elle ne fait^f) en un de matiere pezante^g), ce qui peut faire trouver vos deux experiences veritables quoad sensum^h)3). Car suivant ce calcul et prenant un fort petit espace pour un momant, on pourra trouverⁱ⁾ qu'une boule qui descend de 50 pieds^k), va presque trois fois^l) aussy viste au 2^<d> poulce^m) qu'elle faisoit au premier⁴⁾, et toutefois qu'au 3^esme pied elle ne vaⁿ⁾ pas sensiblemant plus viste qu'au second, et^o) qu'elle ne mettra

+ 18 décembre 1629

1) Mersenne inséra la réfutation de Descartes dans son grand ouvrage à la suite de l'exposé mentionné plus haut: ‘Mais un tres excellent Geometre a demonstré que ce point d'esgalité ne peut se rencontrer suivant la raison precedente. Car, puisque la resistance de l'air ne peut croistre davantage que la vitesse de la cheute, supposons, par exemple....’ (suit tout au long, avec de légères différences, le texte de la lettre de Descartes, depuis la ligne 6 de la page 172 ‘qu'au commencement’ jusqu'à la ligne 24 de la page 172 ‘decenderet’, avec traduction des passages en latin (Harmonie universelle (1636), t. I (1636), Livre III, Prop. 19, pp. 206-207). Quant à cette réfutation par Descartes, à ce moment mal disposé à l'égard de son ancien ami, elle n'était apparemment qu'une chicanerie. Aussi, après sa reconciliation avec Beeckman, il semble avoir oublié entièrement ses objections, et il admet lui-même l'existence d'un point d'égalité dans une lettre à Mersenne de date incertaine, mais de 1634 environ, puis dans une note des alentours de 1635 et dans des lettres à Mersenne du 27 août 1639 et du 30 août 1640 (Oeuvres de Descartes, ed. cit., t. IV (1901), p. 688; t. XI (1909), pp. 629-630; t. II (1898), p. 571 et t. III (1899), pp. 164-165). Galilée aussi admit la possibilité d'un point d'égalité dans la chute des graves dans l'air dans ces Discorsi de 1638 (pp. 75 et 94) et on retrouve l'idée ensuite chez plusieurs savants. Aussi, selon les aéronautes, la hauteur d'où l'on se laisse tomber en parachute serait indifférente.

a) seray point.

b) mandiés cela.

2) Allusion aux premières lignes de la première lettre de Beeckman à Mersenne (ci-avant pp. 141-142). Cf. aussi ci-avant pp. 162-163.

c) L'alinea commença d'abord par la phrase J'ay retiré l'original etc. qui se trouve dans la rédaction définitive plus loin (cf. ci-dessous p. 175).

d) calcul de la resistance de l'air.

e) qu'elle est moins sensible.

f) qu'elle n'est.

g) un poids fort pesante.

h) ad sensum.

3) Cf. ci-avant pp. 167 et 170-171.

i) Car par ce calcul il ne se peut faire qu'une.

k) pieds de haut.

l) trois fois omis.

m) poulce qu'elle descend.

4) Cf. plus haut pp. 154, 160 et plus loin p. 184.

n) ne descendra.

o) et ainsi des autres, en sorte.

[p. 174]

⁺ pas plus de tans à descendre les 25 premiers pieds que les 25 derniers¹⁾, sinon^a) de ce qu'il en fault pour descendre 2 ou 3^b) poulces, ce qui sera du tout^c) insensible. Or cela arrivera^d) principalemant si le poids est de matiere legere^e)2), mais si c'est fer ou plomb^f), l'inegalité du mouvemant ne sera pas si tost insensible; toutefois en une grande hauteur on ne la^g) pourra gueres mieus appercevoir, pour ce que le mouvemant durera moins que d'une matiere legere^h).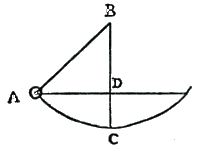

Or ce n'estⁱ⁾ pas de mesme du poids A suspendu en B, lequel va en C³⁾. Car sa descente ne ce^k) doit compter que depuis D jusques à C, qui n'est qu'un poulce ou deus, et vous supposiés^l) un poids de matiere pesante^m)4).

Sans faire d'experience à la tour de Strasbourg, où je n'ay point d'habitudesⁿ⁾, j'oze assurer qu'un poids de matiere pesante descend^o) plus viste qu'un de plus legere, et^p) que, de deus poids de mesme figure et matiere^q), le plus gros descendra le^r) plus viste^s)5).

Pour expliquer qu'^t) une chorde de luth^u) diminue ses retours en proportion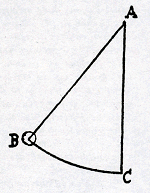



geometrique^v)6), il faudroit dire ce que c'est que la reflexion, ce qui est trop long pour une lettre; mais seulement puis je dire que cete force qui fait retourner la chorde^w), est d'autant plus grande que la chorde est plus tiree hors de sa ligne droite^x), et ^y)qu'estant inesgale, elle rend aussy la diminution des retours inesgale, ce qui est la proportion geometrique⁷⁾. Mais c'est tout autre chose des retours de la chorde AB qui est meue par le poids B; car la pesanteur de ce poids demeure tousjours esgale et ainsy ne cause point d'inegalité en la diminution des retours, lesquelz pour cete cause ne se rencontrent pas ἰσόχρονοι comme les autres⁸⁾.

+ 18 décembre 1629

1) Cf. plus haut pp. 167 et 171.

a) tans aux vingt-cinq premiers pieds qu'aux vingt-cinq derniers, que.

b) cinq ou six poulces.

c) ce qui est.

d) arrive.

e) si ce qui descend est leger.

2) Cf. ci-avant pp. 164, 167 et ci-après p. 184.

f) du fer ou du plomb.

g) du mouvement sera plus grande, mais on ne le pourra.

h) pour ce qu'il descendra plus viste.

i) Or il n'en est.

3) Cf. plus haut pp. 140-141, 164-165 et 167.

k) ne se.

l) vous supposez.

m) pesante auquel par consequent l'air empesche moins; et.

4) Notons à propos des études précédentes sur la loi des mouvements des funépendules, commencées au début de cette année, que ce fut Mersenne qui publia la premier la loi disant ‘que la longueur de la chorde doit estre en raison doublée des temps’ (Harmonie universelle, t. I (1636), Livre II, Prop. 14, p. 133; cf. Livre III, Prop. 20, Coroll. 2, p. 211). Il consacre à ces mouvements plusieurs considérations (ibid., Livre II, Prop. 15, p. 135, t. II (1637), Livre I, Prop. 20, p. 46 et la Premiere Préface générale, p. 4, non numerotée, ainsi que ses Harmonicorum Libri, t. I (1636), Lib. II, Prop. 26, p. 19, suivi de plusieurs problèmes).

n) point de connaissance.

o) descendra.

p) et omis.

q) matiere et figure.

r) le omis.

s) viste. Bref, que de deux poids de mesme matiere et grosseur, mais de differentes figures, celuy duquel la figure approchera le plus du cercle descendra plus viste.

5) Beeckman avait fait cette remarque depuis longtemps (cf. t. I, pp. 31, 175, 196 et 254). Cf. aussi plus haut pp. 123-124, 161, 167 et ci-après p. 184.

t) Vous demandez après pourquoy une.

u) luth tiree hors de sa ligne.

v) geometrique, pour l'expliquer.

6) Cf. plus haut pp. 164 et 167-168.

w) chorde vers sa ligne.

x) droite omis.

y) à partir de ce mot la minute continua ainsi: droite et que cette force se diminuant a mesure que la corde approche de sa ligne fait necessai- rement la proportion geometrique aux mouvemens, au lieu que les retours de la chorde AB, qui est menee par le poids B, ne vont pas en mesme proportion; car la force de la pesanteur demeure toujours egale dans le poids B, et ne se diminue pas comme la force de la reflexion d'une corde de luth. De sorte que vous ne devez pas trouver etrange, si les retours de la corde de luth sont ἰσόχρονοι, et non pas les autres.

7) De bonne heure Mersenne supposait que la raison géométrique des écarts serait 19/20. C'est cette raison, parfois celle de 11/12, que le Minime admet dans ses discussions sur le sujet: Harmonieorum Libri, t. I (1636), Lib. II, Prop. 32, pp. 25-26; Harmonie universelle, t. I (1636), Livre III, Prop. 2, pp. 160-163 et t. II (1637), Livre I, Prop. 17 et 18, pp. 43-46. Dans une lettre non datée, mais probablement de 1634, le mathématicien Beaugrand lui avait calculé les diverses élongations consécutives de la corde tremblante, supposant le rapport 19/20.

8) Plus correct que Beeckman et Galilée (cf. t. III, p. 175, n. 3), Descartes affirme que le temps de l'oscillation doit dépendre de l'amplitude. Mersenne considère ces oscillations ‘proxime’ isochrones dans ses Harmonicorum Libri, t. I (1636), Lib. I, Prop. 26, Coroll. 1, p. 19.

[p. 175]

⁺

....................................

Aus empeschemans de l'aer pour les mouvemans^a)1), il ne fault point consyderer celuy qui suit et celuy qui precede, mais seulemant l'un des deus. Pour^b) le quantum, je l'ignore, et encore qu'il ce^c) pust faire milles^d) experiences pour le trouver à plus^e) pres, toutesfois, pour ce qu'elles ne se peuvent justifier par raison, au moins que je puisse encore atteindre, je ne croy pas qu'on doive prendre la peine de les faire.

Il est certain que les retours de deus chordes qui font la douziesme et sont l'une à l'autre comme 1 à 3^f), se rencontrent ensemble deux fois aussi souvant que celles qui font la quinte et sont l'une à l'autre comme 2 à 3^g)1). J'ay retiré depuis un mois²⁾ l'original du petit traité où je l'explique³⁾, duquel vous avés vu un extrait⁴⁾; il a demeuré unze ans entre les mains du S^r Becman, et si ce tans là suffist pour la prescription, il a droit de se l'attribuer⁵⁾. Or cela des consonances s'explique ainsy^h):

Soynt les chordes A à B comme 3 à 1, et A à C comme 3 à 2; que A employe un momant de tans à faire chasque tour ou retour, et par consequent B ⅓ et C ⅔ⁱ⁾, que donc A et B commencent

+ 18 décembre 1629

a) pour les mouvemans manque.

1) Cf. plus haut pp. 164 et 167-168.

b) et pour.

c) qu'il se.

d) mille.

e) a peu.

f) sont l'une a l'autre comme un a trois, et qui par consequent font la 12.

g) qui sont comme 2 a 3 et qui font la quinte.

2) Date à laquelle les relations entre Descartes et Beeckman furent interrompues et qui est mentionnée par Descartes aussi plus loin p. 195.

3) Cf. le Compendium Musicae dans les Oeuvres de Descartes, ed., cit., t. X (1908), pp. 96-98 et 106.

4) Cf. plus haut pp. 162-163.

5) Cf. ci-dessus p. 173, n. 2.

h) Au lieu de j'ay.... ainsy la minute porta: Et c'est par cela mesme que je prouvois autrefois que la douziesme estoit plus parfaite que la quinte, et la 19^e majeur que la 10 majeur, et celle-cy que la tierce majeur, dans un petit Traitte duquel vous avez veu l'extrait, et duquel j'ay retiré l'original depuis un mois d'entre les mains du S.N., où il estoit depuis onze ans, et ainsi le pouvoit-il appeller sien, au moins si dix ans suffisent pour la prescription. Or cela se prouve ainsi.

i) chordes A et B a la douzieme, et A et C a la quinte, c'est a dire que si pendant un momant A fait un retour, B en fait trois et C en fait un et demy.

[p. 176]

⁺ ensemble à se mouvoir. Pendant que A fera un tour, B en fera trois justemant, et^a) lorsque A commencera son second tour^b), B commencera son quatriesme quand A commencera son 3^e, B son 7^ec). Et ainsy à^d) tous les momans, ils recommanceront ensemble^e), au lieu que, si A et C commencent ensemble à se mouvoir, lorsque A aura achevé son premier tour^f), C sera à la moitié de son second, et ainsy^g) ne sera pas prest de recommancer avec A^h) au 2^<d> momant, mais seulemant au troisiesme, carⁱ⁾ pendant que A aura fait 2 tours^k), C en aura fait 3 justemant^l). Ainsy donc ilz ne recommencent ensemble^m) que deⁿ⁾ 2 momans en 2 momans, au lieu que les precedens^o) recommancent ensemble à tous les momans, ce qui fait que les sons se meslent mieus et font une plus douce harmonie^p)1).

....................................

+ 18 décembre 1629-(mi-janvier 1630]

a) A parachevera son tour, B achever ces trois tours, a sçavoir chacun en un tiers de moment. Et ainsi au second moment.

b) retour.

c) quatriesme; et au troisiesme retour d' A, B fera son septieme.

d) Et ainsy au commencement de tous.

e) commenceront ensemble a se mouvoir.

f) retour.

g) ainsi il ne.

h) avec luy.

i) pource que.

k) retours.

l) justement manque.

m) recommenceront ensemble a se mouvoir.

n) de omis.

o) au lieu que tous les autres.

p) se meslent plu doucement ensemble.

1) Cf. les rèflexions sur la douceur des consonances que Beeckman avait notées il y avait longtemps (t. I, pp. 52-54) et celles dans sa lettre de juin 1629 (pp. 146-147 et du 1^er octobre 1629 (pp. 157-158).

Pierre Serrurier²⁾, à Amsterdam, à Justinus van Assche, à Middelbourg.
25 décembre 1629

Amsterdam, Bibl. de l'Eglise rémontrante (cf. plus haut p. 75). - Autographe.

.......................................

De rerum tuarum successu quod scribis et de repulsâ quam tulisti Dordrechti³⁾, non parùm tecum contristor et doleo. Sed quemadmodum hactenus Deus ex omnibus te expedivit difficultatibus et quae contraria videbantur in bonum tuum convertit, idem confido adhuc facturum. Quicquid possum precibus, libenter opitulabor, ut in hoc difficili et perplexo negotio tibi devinctus, consilium et sapientia suppeditentur, ut quid agendum sit probè discernas et prudenter exequaris. Saluta plurimum, si licet, afflictionum tuarum consortem⁴⁾ et vide ut, quantum potes, animum ipsius corrobores et consoleris; non enim exigua erunt pericula quibus tibi suum probavit amorem....

2) Petrus Serrarius, né à Londres en 1600, suivit ses parents à Amsterdam. Devenu ministre à Cologne, il montra, comme Van Assche, des sentiments dissidents, tout imprégné des erreurs de Caspar Schwenckfeld ((1489-1561), fréquentant des Anabaptistes; en septembre 1628 le Synode défendit à Serrurier le retour. Le 19 décembre 1628 celui-ci se fit immatriculer à l'Université de Groningue comme étudiant en médecine. Retourné à Amsterdam on y proclama, le 21 octobre 1630, les bans entre lui et Sara Paul d'Offenbach. Pendant sa longue vie, il eut des rapports avec Moriaen (t. III, p. 3), Adam Boreel, Duraeus, Comenius, Spinoza et Oldenbourg et se montra chiliaste dans quelques écrits de controverse. Il mourut vers 1670.

3) A propos du mariage de Van Assche avec Sara Beeckman, soeur d'Isaac et veuve de Jaques van Rentergem (cf. plus haut pp. 144-145).

4) Sara Beeckman.