Kernphysik

3.

Wir kommen jetzt zu den Methoden, die man anwenden kann, um die Kerne einander so weit zu nähern, daß Reaktionen möglich werden. Es war wieder Rutherford, der im Jahre 1919 die ersten derartigen Versuche ausführte. Er ging aus von den α-Strahlen, welche von gewissen radioaktiven Atomen, z.B. von Ra C' geliefert werden. Das sind He-Kerne, welche sich mit einer Geschwindigkeit von 1,92 · 10⁹ cm/sec, also mit etwa 1/16 Lichtgeschwindigkeit bewegen. Die kinetische Energie eines solchen Teilchen ist 10^-5 erg. Verglichen mit den Energien, die im täglichen Leben vorkommen, ist diese Energie also recht klein, auf das einzelne Atom bezogen ist es aber ein sehr großer Betrag. Man sieht das, wenn man etwa ausrechnet, wieviel Energie auf ein chemisches Atomgewicht, also auf 4 g He, entfallen würde, wenn alle Atome sich mit der genannten Geschwindigkeit bewegen würden. Man erhält in diesem Falle 6 · 18¹⁸ erg, und das entspricht einer Energie von rund 200 000 Kilowattstunden. Zum Vergleich sei angeführt, daß bei der Verbrennung von 2 g Wasserstoff (22 Liter unter gewöhnlichem Druck) zu Wasser nur 0,08 Kilowattstunde an Energie frei wird. Um die Energien zu messen, hat man in der

[p. 13]

Kernphysik ein neues Maß eingeführt. Man gibt an, wie groß die Potentialdifferenz in Volt ist, die eine Einheitsladung, z.B. ein Elektron durchlaufen muß, um den darzustellenden Energiebetrag aufzunehmen. In diesen Einheiten, die man Elektronen-Volt (abgekürzt e.V.) nennt, ist die Energie des obengenannten α-Teilchens 7,68 · 10⁶ e.V. Da wir im folgenden bei den Kernprozessen stets mit Energien von der Größenordnung 10⁶ e.V. zu tun haben werden, soll von nun an für 1 Million Elektronen-Volt abkürzend 1 M.e.V. geschrieben werden. Die Energien, welche bei gewöhnlichen chemischen Prozessen auftreten, sind höchstens einige e.V.

Läßt man solche α-Strahlen etwa in Stickstoff eintreten, so verlaufen die Begegnungen eines He-Kernes mit einem N-Kern in großer Überzahl ganz ähnlich wie der Zusammenstoß zweier Billardkugeln. Die Kerne werden mehr oder weniger aus ihrer Richtung abgelenkt, aber sie fliegen nach dem Zusammenstoß wieder unverändert weiter. Ganz gelegentlich aber kommt es vor, daß ein He-Kern nahezu zentral auf einen N-Kern zukommt. Ist das der Fall, dann kommen die Kerne, bevor sie wieder auseinander gehen könnten, sehr nahe zusammen, und dann haben sie Gelegenheit, miteinander zu reagieren. Rutherford beobachtet nämlich, daß bei der Ausführung des geschilderten Versuches in kleiner Menge Strahlen von großem Durchdringungsvermögen neu entstehen, die als Wasserstoffkerne oder Protonen großer Geschwindigkeit gedeutet werden müssen. Man spricht hier von Atomzertrümmerung, es scheint aber geeigneter, den Prozeß als Kernreaktion aufzufassen, die ähnlich wie eine gewöhnliche chemische Reaktion durch eine Gleichung dargestellt werden kann. Diese hat im vorliegenden Falle die Gestalt

[p. 14]

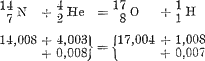
Aus zwei Kernen mit den Ladungen 7 und 2, d.h. aus N und He, sind zwei neue Kerne mit den Ladungen 8 und 1, d.h. O und H entstanden. Dabei ist wie die Gesamtladung, auch die Gesamtmasse, vorausgesetzt, daß man nur die auf ganze Zahlen abgerundeten Atomgewichte beachtet, erhalten geblieben, denn es ist aus N mit dem Atomgewicht 14 und He mit dem Atomgewicht 4, O mit dem Atomgewicht 17 und H mit dem Atomgewicht 1 neu entstanden. Daß wirklich ein stabiles Sauerstoffatom mit dem Atomgewicht 17 existenzfähig ist, ersieht man übrigens aus den Tabellen. Das Gesetz der Erhaltung der Ladung scheint wirklich ohne weiteres ein genaues Naturgesetz zu sein. Das Gesetz der Erhaltung der Masse dagegen ist, wie die Relativitätstheorie uns gelehrt hat, nur dann genau erfüllt, wenn wir die Äquivalenz von Energie und Masse im Sinne der Einsteinschen Beziehung



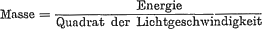
annehmen. Um diese Verhältnisse zu illustrieren, sind unterhalb der Reaktionsgleichung noch die in Frage kommenden Massen genauer angegeben. Auf Einheiten der dritten Dezimale abgerundet hat das N-Atom die Masse 14,008 und das He-Atom die Masse 4,003, dazu kommt aber noch die der kinetischen Energie des α-Teilchens äquivalente Masse von 0,008 Einheiten. Aus dieser Masse entsteht dann das O-Atom mit der Masse 17,004, das H-Atom mit der Masse 1,008, und es stehen nach dem Erhaltungsgesetz dann noch 0,007 Masseneinheiten

[p. 15]

als kinetische Energie der entstandenen Teilchen zur Verfügung. Es besteht nun der sehr bequeme Zusammenhang, daß 0,001 Masseneinheit einer Energie von rund 1 M.e.V. entspricht; die bei der Reaktion freigewordene Energie beträgt danach ungefähr 7 M.e.V., die hauptsächlich dem wegfliegenden Proton zugute kommt. Man sieht, wie vom Standpunkt der Energie eine weit getriebene Genauigkeit der Massenangaben von größter Bedeutung ist. Im vorliegenden Falle, wo die Summe der Atomgewichte links und rechts des Gleichbeitszeichens nahezu gleich ist, kommt das allerdings noch nicht so deutlich zum Ausdruck wie in anderen Reaktionen, welche später betrachtet werden.

Von Rutherford wurden die Teilchen großer Geschwindigkeit nachgewiesen durch Beobachtung des momentanen Aufleuchtens, welches ein mit Zinksulfid belegter Schirm an der Auftreffstelle zeigt. Für die weitere Entwicklung ist es von großer Bedeutung gewesen, daß noch eine andere Methode besteht, mit deren Hilfe man die Bahn der Einzelteilchen photographieren kann. Läßt man die α-Teilchen oder auch Protonen oder Elektronen großer Geschwindigkeit durch mit Wasserdampf übersättigte Luft gehen und expandiert diese, so schlägt sich der Wasserdampf, wie C.T.R. Wilson entdeckte, vorzugsweise nieder um die bei dem Durchgang der Strahlen durch die Luft erzeugten Ionen. Die entstandenen Tröpfchenreihen können bei genügend starker Beleuchtung photographiert werden, ehe sie sich von ihrer Entstehungsstelle entfernt haben. So bekommt man Bilder, in denen man leicht den gewöhnlichen Zusammenstoß von He-Kernen mit N-Kernen zur Darstellung bringen kann. Sehr viel schwieriger war es, die Zertrümmerung zu beobachten. Blackett machte 23 000 Aufnahmen, auf denen im ganzen 415 000 α-Strahlenbahnen photographiert

[p. 16]

waren. Unter diesen fanden sich 8 Fälle, in denen die Bahn eines wegfliegenden Protons beobachtet werden konnte. Wenn 50 000 α-Teilchen in Stickstoff absorbiert werden, so kommt es also nur einmal vor, daß der Kernzusammenstoß zu der durch die Gleichung dargestellten Kernreaktion führt.

Im weiteren Verlauf der Untersuchungen wurden nun die verschiedenen Elemente mit α-Strahlen beschossen und auf eventuelle Zertrümmerung beobachtet, sowohl in Cambridge durch Rutherford und seine Mitarbeiter wie auch in Wien durch Kirsch und Pettersson. Die Resultate sind nicht immer dieselben, die Wiener Beobachter glauben Zertrümmerung bei mehr Elementen festgestellt zu haben, als das von der Cambridger Schule beobachtet wurde. Daß die Zertrümmerung wirklich existiert, darüber aber besteht Einigkeit.