Oeuvres complètes. Tome II. Correspondance 1657-1659

N^o 367.
Cl. Mylon à Fr. van Schooten.
5 janvier 1657.
Appendice au No. 366.

La lettre se trouve à Leiden, coll. Huygens.

A paris ce 5^e Januier 1657.

Monsieur

Lorsque j'estudiois l'Analyse je fis la combinaison des sections coniques, pour voir les Equations qui se pourroient resoudre par jcelles; 1^o. Je joignis la parabole

[p. 3]

et le Cercle, mettant le Centre du Cercle dans l'Axe de la parabole tant du costé du concaue que du conuexe, et fis passer la circonference par le sommet et hors du sommet, toutes ces conjonctions ne donnoient que des Equations planes. mais placeant le Centre du cercle hors de l'Axe si la Circonference passoit au sommet j'auois toutes les Equations Cubiques, si hors du sommet j'auois toutes les quarrequarrées, purgées en ces deux derniers cas de leur plus haut degré. 2^o. Je joignis deux paraboles mettant leurs axes reciproquement parallels a leurs ordonnées, si vne des deux passoit au sommet de l'autre j'auois toutes les Equations Cubiques purgées de leur plus haut degré, si la seconde parabole ne passoit par le sommet de l'autre j'auois toutes les quarréquarrées aussi purgées. 3^o. vnissant l'Axe d'vne parabole auec vne des Asymptotes d'une hyperbole, cela me donnoit des Equations Cubiques purgées, Je ne joignis pas ces deux courbes d'autre maniere, ne doutant point qu'estant jointes autrement elles ne donnassent des Equations quarrequarrées. 4^o. Le Cercle passant par le sommet de l'hyperbole et le centre de ce cercle estant hors de l'Axe, me donnoit des Equations Cubiques affectées du plus haut degrè. Je me contentay aussi de croire, si la Circonference du cercle ne passoit par le sommet de l'hyperbole, que l'on auroit toutes les Equations quarréquarrées sans estre purgées. 5^o. Enfin l'Ellipse et le Cercle passant par son sommet, et dont le Centre estoit hors l'Axe de l'Ellipse, me donnoient des Equations Cubiques non purgées, et sans difficultè si ce cercle ne passe par aucun des sommets de l'Ellipse, jl donnera des quarrequarrées aussi affectées du plus haut degrè, comme en l'hyperbole. Je trouuois aussi que l'Ellipse estoit vn lieu fort determiné et qu'il estoit beaucoup plus limité que l'hyperbole laquelle auec son opposée et ses deux conjuguées ne passoit que pour vn lieu. Monsieur De Roberual me satisfit de cette difficulte, et me dit que l'Ellipse estoit accompagnèe de ses 4. hyperboles qu'elle touchoit aux 4. sommets de leurs axes, et que ces 5. sections pouuoient estre prises pour vn lieu, qu'il falloit considerer six cones rectangles contrepointez



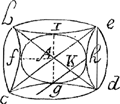a vn mesme sommet, qui font trois couples de Cones opposez comme A b c, A d e; A c d, A e b, Les deux autres Cones ont le mesme sommet A, et touchent les autres, comme celuy de deuant touche les autres par les costez A i, A f, A g, A h, Le sixieme Cone est contrepointe à celuy cy; vn plan pourra couper cinq de ces Cones en sorte que les sections soient deux hyperboles opposées, deux conjuguées, et l'Ellipse qui les touchera toutes 4. aux sommets de leurs axes. Donc si on ne peut resoudre quelques Equations Cubiques par l'jntersection d'vne Ellipse et d'vn Cercle, faut auoir recours a ses 4. hyperboles qui suppléront a son deffaut. Maintenant je considere que l'on peut au trauers de ces 6. cones mener vn plan comme g K h, qui fera pour sections dans les deux cones contigus c A d, c A d deux paraboles egales qui estant opposées s'entretoucheront au sommet commun K, ce mesme plan dans deux autres cones pourra faire deux hyperboles, ou d'autres sections; si donc toutes ces

[p. 4]

dernieres Conisections de ce plan g k h ne sont contées que pour vn lieu, ne suppléeront elle pas au deffaut de la seule parabole dans les cas des Equations ou elle est defectueuse, Je vous prie monsieur de prendre la peine de l'examiner pendant que vous estes dans cette estude, et d'esprouuer premierement si deux paraboles egales contrepointées au mesme sommet de leurs axes, ne font point l'effect entier estant coupées par le Cercle de Monsieur Lepailleur, l'Exemple de l'Ellipse me persuade fort, La parabole sera peut estre de mesme, voyez donc si elle ne demande point le secours de sa compagne, et de ses hyperboles, Jl y a grande liaison entre les Equations et ces sections coniques, aprez cet examen je donne les mains a ce que vous et Monsieur de Zulichom aurez arrestè, Je Luy fais la mesme priere et Luy enuoye celle cy toute ouuerte. Je ne croy pas que vous le trouuiez mauuais, et que vous soyez faschè qu'il lise que je suis

Monsieur

Vostre treshumble et tresobeissant serviteur Mylon.

Messieurs De Carcaui et Bosse¹⁾ vous baisent les mains.

A Monsieur Monsieur De Schooten, professeur demeurant rue heerestede²⁾ A Leyden En hollande.

1) Abraham Bosse, né en 1611 à Tours où il mourut en 1678, était graveur et fort lié avec des Argues, dont il édita les ouvrages. Il fut reçu membre de l'Académie, mais ayant pris le parti de des Argues, il en fut exclu plus tard, à cause de sa violente opposition contre Lebrun.

2) Lisez: Heerensteeg.