Oeuvres complètes. Tome X. Correspondance 1691-1695
(1905)–Christiaan Huygens–
[pagina 17]
| |
No 2660.
| |
[pagina 18]
| |
A la Haye 23 Février 1691. Monsieur
Jay vu avec bien du déplaisir dans vostre derniere lettre que vous avez entendu tout autrement et au contraire de mon intention ce que je vous avois escrit, que vostre excuse estoit merveilleuse. Car j'ay voulu dire par là que cette excuse estoit tout à fait superflue, et que j'estois fort eloignè d'avoir aucun soupçon, que vous eussiez contribuè à ce qu'on avoit mis abusivement dans les Actes de Leipzich à mon prejudice. C'est la pure veritè, et il me semble que par toute sorte de raisons vous deviez l'avoir pris de cette manière. Je n'ay pas encore pu avoir ces Actes des mois de Novembre et Decembre de l'année derniere, de sorte que je ne scay si la faute aura estè reparée. Cependant j'ay fort bien compris depuis ma derniere, comment ma series pour l'Hyperbole se rapporte à celle de vos logarithmes et j'ay aussi trouvè que j'aurois pu apprendre cette series du livre de Mr. Wallis, qu'il a escrit de l'Algebre en AngloisGa naar voetnoot3) p. 329, où il range la progression de Mercator et la siene l'une au dessus de l'autre conjointement, qui estant adjoutées ensemble sont le double de la progression a+⅓ a3+⅕ a5 &c., de mesme que vous le faites voir dans vostre lettre du 25 Nov.Ga naar voetnoot4). Je m'etonne que Mr. Wallis n'ait pas remarquè cela, ni combien cette progression doublée est plus utile pour la quadrature de l'Hyperbole et pour trouver les Logarithmes que n'est la sienne ni celle de MercatorGa naar voetnoot5), car le calcul en devient plus court de la moitiéGa naar voetnoot6). Depuis quinze jours j'ay revuGa naar voetnoot7), non sans peine, les brouillons que j'avois touchant les mouvements à travers un milieu qui fait resistence, scavoir dans la vraye hypothese, et j'ay fait quelques calculs en suite, pour voir comment ils s'accorderoient avec les vostresGa naar voetnoot8). Je trouve qu'une partie de nostre dispute vient de ce que vous prenez le mot de resistence dans une autre signification que moy et Mr. Newton; car vous appellez resistence la velocitè perdue ou la perte de velo- | |
[pagina 19]
| |
cité causée par le milieu, ou la velocitè perdue, et en consequence de cela pour comparer des resistences differentes, vous voulez que la consideration des elemens du temps entre en compte, et qu'à parler exactement, on ne doit pas dire que les resistences sont en raison des velocitez, ni en raison des quarrez des velocitez. En quoy il est evident que vous prenez l'effet de la resistence pour la resistence mesme. Mais à Mr. Newton et à moy la resistence est la pression du milieu contre la surface d'un corps, comme par exemple, quand on tient dans la main une feuille de carton, et qu'on l'agite à travers l'air, on sent une pression qui se peut comparer à celle d'un poids, et qui devient quatre fois plus grande lorsqu'on remue cette feuille deux fois plus viste qu'auparavant, ainsi que j'ay trouvè autre fois à Paris par des experiences fort exactesGa naar voetnoot9). Vous voiez, Monsieur qu'il n'y a que la differente vitesse dont depend cette pression, sans considerer des parties egales ni inegales des temps. Et c'est sans doute la veritable et la plus naturelle notion de la resistence. Je comprens bien pourtant comment, suivant la vostre, vous voulez conserver l'inscription de vostre article 5, mais c'est comme j'ay dit, en prenant l'effet pour la cause, et toute l'obscuritè de vostre discours vient principalement d'icy; laquelle, à ce que je crois, est cause que personne ne l'a assez examinè pour comprendre ce qu'il y a de vray, ni pour remarquer les abus que vous y corrigez maintenant vous mesme. J'avois fait la mesme correction mot à mot dans la prop. 3. art. 5, que vous m'envoiez dans vostre derniere lettre. A la prop. 6. du mesme article les espaces parcourus, qui à moy sont comme les logarithmes de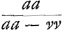 , selon vous sont comme les logarithmes de , selon vous sont comme les logarithmes de 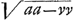 (il falloit (il falloit 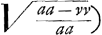 ou de √(1-vv); ce qui revient pourtant à la mesme chose, (si non que vos logarithmes devienent negatifs) car les logarithmes des racines ont entre eux la mesme raison que ceux de leurs quarrez. Vous aviez de mesme des logarithmes negatifs, en disant que les temps sont comme des logarithmes de ou de √(1-vv); ce qui revient pourtant à la mesme chose, (si non que vos logarithmes devienent negatifs) car les logarithmes des racines ont entre eux la mesme raison que ceux de leurs quarrez. Vous aviez de mesme des logarithmes negatifs, en disant que les temps sont comme des logarithmes de 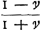 , mais dans vostre derniere vous l'avez redressè en mettant , mais dans vostre derniere vous l'avez redressè en mettant 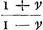 . Je m'apperçois assez, Monsieur, en tout cela, qu'il ne vous manque ni habilitè ni science pour demesler toute cette matiere, et d'autres plus difficiles, mais que seulement vous n'avez pas assez de loisir pour adjouter plus d'exactitude et de clartè aux choses que vous avez trouuées. . Je m'apperçois assez, Monsieur, en tout cela, qu'il ne vous manque ni habilitè ni science pour demesler toute cette matiere, et d'autres plus difficiles, mais que seulement vous n'avez pas assez de loisir pour adjouter plus d'exactitude et de clartè aux choses que vous avez trouuées.
| |
[pagina 20]
| |
Je ne scay pas pourquoy dans tout ce discours de la Resistence vous n'avez rien voulu determiner des choses qui sont comme le fruit de cette recherche, et qu'on peut souhaiter de scavoir, comme si quaeratur tempus descensus liberi ad tempus descensus impediti donec data celeritas obtineatur, hoc est, quae ad celeritatem terminalem datam rationem habeatGa naar voetnoot10); aut si quaeratur ratio spatiorum sic per actorumGa naar voetnoot11); item quae sit ratio temporis ascensus ad tempus descensus, cum corpus recta sursum projicitur celeritate terminaliGa naar voetnoot12). Je souhaiterais de voir comment vos calculs s'accordent aux miens dans ces problemes, et en les comparant ensemble nous pourrions estre assurez tous deux d'avoir raisonnè juste. Le Traité de Mr. Newton en cecy n'est pas sans fauteGa naar voetnoot13). Dans l'art. 6. prop. 1. vous faites la ligne du jet bien plus facile à trouver qu'elle n'est en effet, sur quoy je vous prie d'examiner la remarque que j'ay faite dans l'addition à mon discours de la PesanteurGa naar voetnoot14). J'ay considerè vostre construction de la Courbe Exponentiale qui est fort bonne. Toutefois je ne vois pas encore que cette expression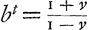 soit d'un grand secours pour sela. Il y a longtemps que je connois cette mesme courbeGa naar voetnoot15) aussi soit d'un grand secours pour sela. Il y a longtemps que je connois cette mesme courbeGa naar voetnoot15) aussi
| |
[pagina 21]
| |
bien que sa compagneGa naar voetnoot16), qui sert aux jets montans, et je la construis par la ligne logarithmique en supposant les velocitez données au lieu que vous supposez les temps. Quoyque cette lettre soit desia bien longue, il faut que je vous responde à ce que vous souhaitez de scavoir touchant la methode des Tangentes de Mr. Fatio. Vous scaurez donc que l'auteur est depuis quelque temps en cette ville et qu'il me fait souvent l'honneur de me voir. J'avois examinè sa lettre dont je vous ay parlè, où la dite methode estoit amenée jusqu'a un certain point, mais depuis qu'il est icy, il l'a beaucoup perfectionnée, et m'a trouvè les deux mesmes courbes dont je vous avois proposè les soutangentesGa naar voetnoot17), desquelles la 2. a plus de difficultè. Ses calculs ne sont pas longs, ni n'ont besoin d'aucunes Tables, mais il ne scauroit resoudre jusqu'icy les cas, où il entre des racines qui contienent des inconnues et plus d'un terme; par exemple si la soustangente est donnée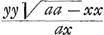 , x estant l'abscisse, y l'appliquée à angles droits et a une ligne connue. Si vostre methode ne s'arreste pas à ces racines, vous avez quelque chose de plus que Mr. Fatio, quoy qu'il ait desia passè mon attente. Peut-estre c'est pour ces racines que les Tables, dont vous parlez, sont necessaires dans la methode que vous dites reussir toujours. , x estant l'abscisse, y l'appliquée à angles droits et a une ligne connue. Si vostre methode ne s'arreste pas à ces racines, vous avez quelque chose de plus que Mr. Fatio, quoy qu'il ait desia passè mon attente. Peut-estre c'est pour ces racines que les Tables, dont vous parlez, sont necessaires dans la methode que vous dites reussir toujours.
Cette quadrature de la 1e de mes courbesGa naar voetnoot18), que vous dites estre aisée, marque aussi quelque connoissance extraordinaire. Vous me ferez plaisir de la determiner, à fin que Mr. Fatio se puisse assurer que vous l'avez trouvée, à quoy il m'a avouè n'avoir pu reussir. La figure, au reste, de cette courbe ne consiste pas dans | |
[pagina 22]
| |
les seules 2 demi-ovales, comme je vous avois marquèGa naar voetnoot19), mais elles sont jointes par une croix et le tout ressemble à un 8, ce qui se connoit aisement par l'equation. Quant à la courbe exponentialeGa naar voetnoot20) que vous trouvastes au lieu de cette ligneGa naar voetnoot21), lorsque les signes+et-estoient renversez, Mr. Fatio assure, et m'a demonstrè en quelque façon, que cette exponentiale est impossibile, par où vous voyez que vostre demonstration pour prouver qu'elle satisfait à la soutangente donnée, ne nous est pas claire. Vous m'obligerez d'achever ce que vous avez trouvè sur la chaine pendante, afin que nous nous communiquions nos meditations. Je crois qu'il y aura bien d'autres geometres qui resoudront ce probleme, car, à dire vray, il ne me paroit pas bien difficile, si ce n'est que vous en demandiez quelque chose de plus que ce que j'en ay trouvé. Ga naar voetnoot22) Mr. Spener m'a dit que, pour faire reussir la boule de souphre de Mr. Guericke, il faut adjouter pour chaque livre 13 grains salis tartari fixi; peut estre l'autheur vous aura donné la mesme recepte. Il me dit aussi qu'il pouvoit oster au fer l'attraction vers l'aimant, mais je ne m'y fie pas trop depuis que j'ay trouve fausse une experience avec le vif argent, qu'il debitoit comme tres certaineGa naar voetnoot23). Ce n'est pas sans regret que je perds l'esperance de vous voir icy, et je n'aurois pas esté si longtemps sans vous escrire si je ne vous avois tousjours attendu. Je suis Monsieur etc. |
|