Oeuvres complètes. Tome X. Correspondance 1691-1695

[p. 572]

N^o 2841.
G.W. Leibniz à Christiaan Huygens.
11 décembre 1693.

La lettre se trouve à Leiden, coll. Huygens.
Elle a été publiée par P.J. Uylenbroek¹⁾ et C.I. Gerhardt²⁾.
Elle fait suite au No. 2829.
Chr. Huygens y répondit par sa lettre du 29 mai 1694.

Hanover ce 1/11 décembre 1693.

Monsieur

Vous aurés receu la lettre assez ample que je me suis donné l'honneur de vous écrire, il y a plusieurs semaines. Cependant vous aurés receu aussi les Actes de Leipzig, tant le mois ou mon effection des quadratures par le mouuement est inserée³⁾, que celuy ou vostre solution du probleme de Mr. Bernoulli⁴⁾ se trouue avec mon apostille⁵⁾, dont j'espere que vous ne serés pas mal satisfait. Je souhaitte surtout que vous nous expliquiés bientost vostre ligne enigmatique.

Quand je vous ecrivois ma derniere, je n'avois pas encor vu l'Histoire des ouvrages des Sçavans de cette année, il est vray que j'avois fait prier M. Desbordes⁶⁾ de me les envoyer, avec d'autres livres, lorsque le libraire, qui a imprimé le premier tome de mon Code diplomatique⁷⁾ lui en envoyoit quelques exemplaires. Mais M. Desbordes n'a pas encor satisfait au libraire⁸⁾, et envoya quelques unes des choses que j'avois demandées à Mons. de la Bergerie, Ministre françois de la religion reformée⁹⁾, le quel ne sçachant point que c'estoit à mon occasion, crût que c'estoit pour luy et les garda. Ce ne fut que depuis peu et par hazard que je le sçus. Car c'estoit par l'entremise de Mr. de la Bergerie que mon libraire avoit envoyé les exemplaires à M. Desbordes, et comme je m'estois ensin informé du retardement, il se trouva que Mr. de la Bergerie avoit receu quelques unes des pieces que j'avois souhaittées et entre autres l'Histoire des ouurages des Sçavans.

1) Chr. Hugenii etc. Exercitationes Mathematicae, Fasc. I, p. 169.

2) Leibnizens Mathematische Schriften, Band II, p. 167, et Briefwechsel, p. 723.

3) L'article cité dans la note 6 de la pièce N^o. 2824.

4) La pièce N^o. 2823.

5) La pièce N^o. 2824.

6) Parmi les nombreux réfugiés français de ce nom habitant les Pays-Bas, nous n'avons pu identifier le personnage en question.

7) Voir, sur cet ouvrage, la note 7 de la Lettre N^o. 2797.

8) Samuel Ammon.

9) Claude Guillaume de la Bergerie, chapelain de l'Electrice de Brunswick-Luneburg. Il atteignit l'âge de 84 ans et fut inhumé à Hanover le 6 août 1743.

[p. 573]

En ayant lu le mois de feurier, j'ay vu que je vous devois des remercimens de l'honnesteté avec la quelle vous avés bien voulu faire une mention avantageuse de mon calcul¹⁰⁾. Je dirai seulement un mot de la difference que vous mettés¹¹⁾, Monsieur, entre ma construction des logarithmes par la Chainette, et entre celle que vous en donnés par la traction; en disant que par la traction le parametre de la courbe, qui est sa tangente universelle, est donné, au lieu que je n'avois point enseigné, selon vous, comment on pourroit trouuer le parametre de la Chainette. Cela est venu sans doute de ce que vous n'aviés pas alors le loisir de jetter les yeux sur ma figure¹²⁾, car vous auriés pu juger d'abord que la description de la courbe par le moyen d'une chainette en donne aussi fort aisement le parametre. Car la



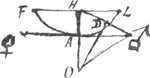ligne FAL estant formée par le moyen de la chainette donnée ♀♂ suspendue par les deux bouts F et L, posés dans une meme horizontale, dont le milieu soit H, et le sommet de la chainette A, joignons H ♂, et de son milieu D menons à angles droits une droite DO, qui rencontrera HA prolongée en O, et AO sera le parametre qu'on demande. Car j'avois déja remarqué dans les Actes de Leipzig, en donnant l'explication de la chainette, que lors qu'on fait A ♂ egale à la courbe AL, il se trouue aussi qu'OH et O ♂ sont egales¹³⁾. Ainsi puisque dans cette description de la courbe, sa longueur, sçavoir celle de la chainette qui sert à la description, est donnée aussi, il est aisé d'en trouuer encore le parametre. Je ne laisse pas de preferer la construction de la Traction non pas tant à cause des Logarithmes, qu'a cause des consequences qui sont d'une grande étendue, puisqu'elle sert à construire toutes les quadratures par un mouuement exact et regle¹⁴⁾, dont je souhaitte d'apprendre vostre jugement.

Je souhaitte aussi que vous fassiés part au public de vos nouuelles lumieres sur l'attraction electrique¹⁵⁾, et que nous puissions jouir enfin de vostre dioptrique¹⁶⁾; ou j'espere que nous trouuerons bien des choses considerables touchant les Me-

10) Voir la pièce N^o. 2793 à la page 407.

11) Voir les pages 412 et 413 de la pièce N^o. 2793.

12) Il s'agit de la figure de l'article de Leibniz cité dans la note 1 de la pièce N^o. 2681, laquelle se trouve reproduite sans modification essentielle dans la Lettre N^o. 2688.

13) Voyez l'article cité dans la note précédente sous l'en-tête: ‘Rectam invenire arcui catenae aequalem’, ou bien la Lettre N^o. 2688 à la page III.

14) Voir la note 7 de la pièce N^o. 2824.

15) Comparez la Lettre N^o. 2633, du 18 novembre 1690, à la page 539, et la Lettre N^o. 2643, à la page 572. En 1692 Huygens s'est occupé encore d'expériences électriques en étudiant les effets d'attraction et de répulsion produits sur des flocons de coton et d'autres corps légers par une boule d'ambre d'environ un pouce de diamètre. Il les a consignées dans le Livre G des Adversaria, pages 44 et 45, et tâché d'en rendre raison en supposant qu'un corps électrisé est entouré d'un tourbillon. Il paraît, par une note, qu'il a repris ces expériences le 27 décembre 1693.

16) Comparez la Lettre N^o. 2784.

[p. 574]

teores emphatiques¹⁷⁾. J'ay tousjours eu du panchant à croire que les queues des cometes sont de ce nombre, quoyque les explications qu'on en a données jusqu'icy ne soyent point satisfaisantes, et que je n'aye pas non plus de quoy me satisfaire le dessus. Enfin je souhaitte en mon particulier vos reflexions sur quelques considerations physiques d'une de mes precedentes¹⁸⁾, que vous m'aviés fait esperer dans vostre derniere¹⁹⁾.

On me mande de Paris qu'on y a donné au public, à l'imprimerie du Louure et des MS. de la Bibliotheque du Roy, quelques anciens Mathematiciens Grecs. Entre autres Athenaeum de Machinis, des Extraits poliorcetiques d'Apollodore, et quelques ouurages de Philon, et de Biton de la construction des machines de guerre, et les Cestes de Julius Africanus. On adjoute qu'un nommé Mons. Boivin, a eu soin de cette edition²⁰⁾, estant sçavant dans le Grec, mais que Mr. de la Hire en a esté chargé comme Mathematicien. Mais on dit en même temps que l'ouurage aurait esté plus exemt de fautes, si un seul, qui eut eu l'habileté de ces deux sçavans hommes, eut eu la direction de cette Edition.

Quand Monsieur le Marquis de l'Hospital m'ecrivit il y a quelques mois²¹⁾, il me demanda, si je n'avois pas reglé la ligne isochrone, à l'egard de l'eloignement uniforme d'un point fixe que j'avois proposé²²⁾. Je me souuenois d'avoir vû

17) Cette division des phénomènes célestes en phénomènes emphatiques (ϰατ᾽ ἔμφασιν), dus, comme l'arc-en-ciel, à quelque réflexion de la lumière, et en phénomènes substantiels (ϰατ᾽ ὑπόστασιν), comme les étoiles filantes, est empruntée probablement à l'ouvrage pseudoaristotélique ‘De Mundo’, Cap. IV. (Aristdt. Ed. Didot. Vol. III, p. 683).

18) Voir la Lettre N^o. 2797.

19) La Lettre N^o. 2822, à la page 509.

20) Veterum Mathematicorum Athenaei, Bitonis, Apollodorii, Heronis, Philonis, et aliorum Opera, Graece et Latina pleraque nunc primum edita. Ex Manuscriptis Codicibus Bibliothecae Regiae. Parisiis, ex Typographia Regia. mdcxciii. in-f^o. L'ouvrage a été commencé par Thevenot et achevé par J. Boivin et Ph. de la Hire.
Jean Boivin de Ville-neuve, né à Montrenil-l'Argilé le 28 mars 1663, obtint en 1692 une place à la Bibliothèque du Roy, où il découvrit et déchiffra un manuscrit palimpseste, contenant la Bible. Il devint professeur de Grec au collège royal et fut membre de l'Académie des inscriptions (1705) et de l'Académie française (1721). Il mourut le 29 octobre 1726.

21) Il s'agit de la Lettre du 24 février 1693, publiée par C.I. Gerhardt dans le Tome II de ‘Leibnizens Mathematische Schriften’, p. 223-227, voir la page 224. Voir encore la note 23.

22) Leibniz l'avait fait vers la fin de l'article d'avril 1689 cité dans la note 2 de la Lettre N^o. 2512, et dans les termes suivants: ‘invenire lineam, in qua descendens grave recedat uniformiter a puncto dato, vel ad ipsum accedat’, défiant les Cartésiens à en chercher la solution par leur analyse. Et il répéta ce défi dans les articles des Acta de mai et de juillet 1690, cités dans les Lettres N^o. 2640, note 5, et N^o. 2623, note 10.
La question d'ailleurs était des plus difficiles pour l'époque, puisqu'elle mène, même dans le cas particulier auquel on s'est borné ordinairement, à une intégrale elliptique, qui ne peut être réduite ni à la quadrature de l'hyperbole, c'est-à-dire aux logarithmes, ni à celle du cercle. Aussi, ce ne fut que cinq ans après qu'elle avait été posée que Jacques Bernoulli l'entama dans les Acta de juin 1694 sous le titre: ‘Jac. B. Solutio problematis Leibnitiani de Curva Accessus & Recessus aequabilis a puncto dato, mediante rectificatione Curvae Elasticae’. Puis, dans les Acta d'août 1694, Leibniz publia sa propre solution sous le titre: ‘G.G.L. Constructio propria problematis de Curva Isochrona Paracentrica. Ubi & generaliora quaedam de natura & calculo differentiali osculorum, & de constructione linearum transcendentium, una maxime geometrica, altera mechanica quidem, sed generalissima. Accessit modus reddendi inventiones transcendentium linearum universales, ut quemvis casum comprehendant, & transeant per punctum datum’. Elle fut reprise ensuite par Jacques Bernoulli dans les Acta de septembre 1694 dans l'article: Jac. B. Constructio Curvae Accessus & Recessus aequabilis, ope rectificationis Curvae cujusdam Algebraicae, addenda nuperae Solutioni mensis Junii’. Enfin dans ceux d'octobre, Jean Bernoulli publia sa ‘Constructio facilis Curvae accessus aequabilis a puncto dato per Rectificationem curvae Algebraicae’.

[p. 575]

le moyen d'y arriver, mais je n'avois pas alors le loisir d'y penser, comme je temoignais dans ma reponse à Monsieur le Marquis²³⁾. Depuis ayant retrouué un vieux brouillon, j'ay vu que je l'avois reduit à une quadrature, qu'il faudra examiner avec plus d'attention, pour voir s'il n'y a pas la dessus quelque chose de reduisible à la commune Geometrie²⁴⁾. Je ne sçay si le silence que Mr. le Marquis a gardée depuis²⁵⁾, ne marque point que ma lettre ne l'a point satisfait. Comme en

23) Dans la première de ses Lettres à Leibniz, celle du 14 décembre 1692, de l'Hospital lui avait écrit qu'il ne savait pas encore trouver le moyen de décrire la courbe, définie par l'équation différentielle a²xdx+2y³dy=2a²xdy-a²ydx; quoiqu'il s'y fût beaucoup appliqué à cause que cette courbe avait des propriétés considérables. Alors Leibniz, dans sa réponse dont la date est inconnue, lui apprit à résoudre une telle équation au moyen de séries infinies dont on pouvait calculer autant de termes qu'on voudrait, comme, par exemple celle en question (posant a=1) par la série:x=y-⅖y³-4/75y⁵-64/4875y⁷ (lisez-64/5625y⁷) etc., ou bien par une plus générale renfermant aussi des ‘termes pairs’. Ensuite, dans sa lettre du 24 février 1693, citée dans la note 21, de l'Hospital remarque que l'équation différentielle mentionnée exprimait dans un cas particulier la courbe de descente ‘que vous avez proposée autrefois aux Cartésiens’, montrant comment il était arrivé à cette équation dans ses recherches sur cette courbe. Enfin, dans une lettre de date inconnue, Leibniz lui répondit: ‘Je suis bien aise de sçavoir que l'équation differentielle que vous m'avés en voyée, Monsieur, sert pour un cas de la ligne ou le poids descendant s'éloigne egalement d'un certain point Cela me servira à y mieux penser un jour. Car autres fois songeant à ce probleme je croyois voir quelque chemin pour le donner’.

24) D'après la solution de Leibniz mentionnée dans la note 22, il s'agit de la quadrature représentée par l'intégrale: ∫a²dz/√az(a²-z²), irréduisible, comme on le sait maintenant, à la ‘commune Géométrie’, puisque c'est une intégrale elliptique.

25) Toutefois de l'Hospital n'avait pas tardé à répondre à la lettre de Leibniz par la sienne du 23 avril 1693, dans laquelle le problème de la courbe isochrone n'est plus mentionné; mais d'après la publication de Gerhardt, il y a eu en effet une interruption dans le commerce de lettres de de l'Hospital avec Leibniz depuis celle du 15 juin 1693 jusqu'à celle du 30 novembre 1694.

[p. 576]

effect cela ne sçauroit manquer d'arriver à l'egard de celles d'un homme qui se laisse distraire autant que moy. Cependant je n'en estime pas moins Mons. le Marquis de l'Hospital, et je trouve que vous avés eu raison, Monsieur, de luy rendre justice dans vostre lettre à Mr. de Beauval²⁶⁾. Je m'étonne qu'il est presque le seul en France qui entre dans la Geometrie profonde. Connoissés vous Mr. Rolle?²⁷⁾ il semble que c'est luy qui a fait proposer un probleme geometrique avec un prix²⁸⁾, mais à condition qu'on le doit resoudre par des voyes différentes de celles que Mr. Rolle a publiées²⁹⁾. Je n'ay jamais vû ces voyes, et je ne m'amuseray pas à ce probleme, qui est trouuer la plus simple courbe, propre à construire l'equation donnée avec une courbe donnée. Mr. Bernoulli le cadet a donné sa Methode la dessus³⁰⁾. On a temoigné qu'on n'en estoit point content³¹⁾. Je crois que Mr. Bernoulli y repliquera bientost³²⁾. Ce n'est pas une chose si difficile à une personne aussi versée, qu'il l'est, dans cette Analyse. Pour moy j'avois cru

26) Voir la pièce N^o. 2793 aux pages 407, 416 et 417.

27) Voir, sur Michel Rolle, la note 5 de la Lettre N^o. 2454.

28) Voici l'‘Avis aux Geometres’ que l'on trouve dans le Journal des Sçavans du 20 juillet 1693: ‘On a deposé un prix de soixante pistoles chez M. le Normand Notaire au Châtelet de Paris, pour la premiere personne qui résoudra la question suivante.
Ayant une partie si petite qu'on voudra d'une courbe Geometrique, on demande une metode pour resoudre une égalité donnée par le moyen de cette partie, & d'une autre ligne courbe dont le lieu soit le plus simple qu'il sera possible.
L'on demande aussi que cette metode paroisse publiquement avant le premier Janvier prochain, & qu'elle ne suppose aucune des regles qui sont de l'invention particuliere de M. Rolle.
Mons. Descartes a proposé ce probleme pour une des trois sections coniques seulement, & on n'en avoit jamais proposé un plus beau pour la resolution des egalitez. De plus cette resolution estant absolument necessaire pour perfectionner toutes les parties des Mathematiques, il importe de scavoir s'il n'y a point pour cela de metode qui soit differente de celles que Mr. Rolle a données au public’.

29) Voir l'ouvrage cité dans la note 25 de la Lettre N^o. 2709.

30) Dans le Journal des Scavans du 31 août 1693, sous le titre: ‘Solution d'un Probleme proposé dans le 28. Journal de cette année, page 336. Par Mr. Bernoulli le Medecin’.

31) Voir l'article anonyme du Journal des Sçavans du 14 septembre 1693, intitulé: ‘Reponse à Mr. Bernoulli le Medecin, au sujet d'une metode qui a paru sous son nom dans le Journal du 31. août dernier’.

32) C'est ce qu'il fit en effet dans le Journal du 18 janvier 1694 sous le titre: ‘Response de M. Bernoulli le Medecin, à l'objection inserée dans le Journal du 14 Septembre dernier, contre une metode qui a paru de lui dans le Journal du moi d'Août précedent’. L'anonyme (sans doute Rolle lui-même) duplique dans le Journal du 15 février par l'article ‘Remarques sur la Réponse qui a esté inserée sous le nom de M. Bernoulli dans le 3 Journal de cette année, au sujet d'un problème de Geometrie’, prétendant ‘que M. Bernoulli n'a point satisfait aux difficultez capitales du problème, & mesme que l'on seroit infiniment éloigné d'y satisfaire par les metodes qu'il a citées pour ce sujet’.

[p. 577]

que cette matiere estoit comme epuisée, et qu'il ne s'agissoit que d'en donner les canons pour epargner aux autres la peine du calcul. Je suis avec zele

Monsieur

Vostre treshumble et tres obeissant serviteur Leibniz.