|
| |
| |
| |
VI.
[1646].
La pièce a été publiée par P.J. Uylenbroek.Ga naar voetnoot1)
De Catena pendente.Ga naar voetnoot2)
Theorema 1.mum Si pondus suspendatur ex duobus funibus, hi producti secabunt sese in pendula ponderis gravitatis diametro.
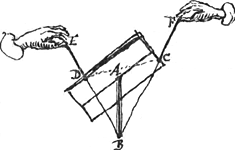
Sit pondus DAC cujus pendula gravitatis diameter AB; suspensum ex funibus ED, FC, ligatis in punctis C et D; dico, si-prolongentur ii funes, intersecturos se invicem in B, puncto, quod est in pendula gravitatis diametro.
Intelligatur enim primo EB, FB duo esse funes in B annexi extremitati bacilli BA, cujus alteri extremitati affixum sit pondus DAC ex suae gravitatis centro A, et bacillus AB horizonti
| |
| |
perpendicularis, ita ut pondus DAC bacillo innitatur, bacillus vero in puncto B duobus funibus EB, FB, quorum ligatura in D et C omnino soluta sit; manifestum itaque est pondus sic suspensum, non decisurum ad hanc vel illam partem: Admo-
| |
| |
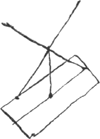
veantur nunc funes EB, FB, punctis D et C ibique firmentur, et tamen pondus in eodem situ manebit; At jam non amplius baculo neque puncto B innitetur sed suspensum erit ex funibus ED, FC, et hi producti in pendula gravitatis diametro se intersecant; quod erat probandum.
Alterum hunc casum Stevinius bene demonstravit.Ga naar voetnoot3)
Sequitur ex hoc theoremate quod si in fune EDACF, nexa sint pondera G et H aequalia, in punctis D et C, haec non
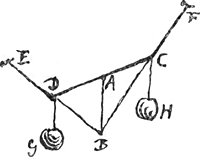
posse ullo sito pendere nisi ut productae ED, FC concurrant in eodem puncto B quod in eorum pendula gravitatis diametro sit, quae diameter si pondera aequalia sint secat partem funis interjectam inter ponderum ligaturas D, C, in duas aequales partes; si autem D majus esset H, secaret ipsam DC, ita ut pars AD esset ad pondus H, ut pars AC ad pondus G.
Si enim DC rigidum supponatur apparet ex praecedenti theoremate non posse pondera alio situ suspensa manere nisi ut ED, FC productae conveniant in eodem puncto cum gravitatis diametro; at in eo situ
| |
| |
non manerent, nisi eorum centrum gravitatis A tunc centro terrae quam proxime potest admotum esset Ga naar voetnoot4); ergo et hic ubi DC rigida non est sed tamen tensa semper ut et aliae ED, FC, apparet centrum eorum gravitatis A centro terrae propius
admoveri non posse, ac proinde quoque praedicto situ suspensa manere debere.
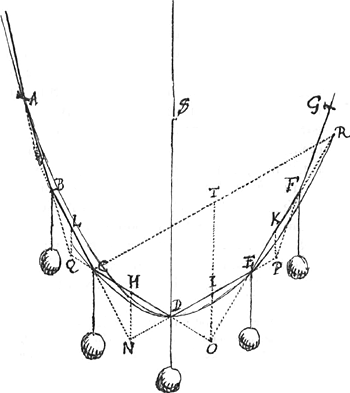
Propos. 2. Propositus nunc sit funis ADG in quo aequalibus intervallis ligata sunt aequalia pondera.
Manifestum itaque est eo situ ea pendere debere ut bina quaeque internodia, relicto uno intermedio, producta, sese intersecent in pendula duorum ponderum, gravitatis diametro: Sic BC, ED sese intersecant in puncto N, quod est in pendul. gr. diametro ponderum suspensorum ex C et D. dicantur enim BC et ED invicem non secare in N: Si ergo firmentur puncta B et E in eisdem punctis ubi nunc pendent, hoc quidem situm punctorum C et D nihil immutabit; sed firmatis iis, pondera ex
| |
| |
C et D aliter non possunt suspendi quam ut intersecttio productarum BC, ED sit in pend. grav. diametro, ergo apparet et ante sic suspensa fuisse.
Eodem modo demonstrari potest, AB et DC se intersecare in pend. gr. diametro ponderum ex B et C pendentium, et ita de quotlibet aliis in infinitum ascendentibus. Facile hinc erit, si nota habeamus tria puncta C, D et E catenae hujus, caetera quoque invenire ut B, F, A, G. Oportet enim DE bifariam dividere in I et agere IO parallelam ipsi SD, et ex O, ubi producta CD illam IO secat, per E ducere OF et ponere EF aequalem DE, et habebimus punctum F. Simili modo et reliqua reperiri possunt.
Prop. 3. Linea quae per haec puncta ducitur valde parum distare videtur a linea parabolica, quam tamen non refert.Ga naar voetnoot5) Quod sic demonstrabitur.
Describatur per puncta C, D, E, parabola CDERGa naar voetnoot6), dico hanc non transire per punctum F. Fiat enim ut OD ad DC sic OE ad ER, quae signetur in OEF productâ, dico primò punctum R esse in eadem linea parabolica cum punctis C, D, E; producatur enim OI, ducaturque CR quae ipsam secet in T; et quoniam est DC ad ER ut OD ad OE, linea autem OT secat ipsam DE bifariam, manifestum quoque est ipsam CR bifariam sectam in T; porro cum puncta C, D, E, sint in parabola, et CT aequalis TR et CR aequidistans ipsi DE necessario quoque punctum R erit in eadem parabolica linea, alias enim OT non esset parabolae diameter per 28 Con. Apoll. lib. 2Ga naar voetnoot7). quod absurdum esset quia axi DS parallela est ex constructione. Cum itaque punctum R sit in parabolica linea eadem in qua est punctum E, sequitur punctum F in ea non posse esse, quia deberet recta linea OR parabolam in tribus punctis secare quod absurdum est: vel punctum R coincidere cum puncto F, quod impossibile est, cum OE semper major sit ODGa naar voetnoot8), et quam proportionem habet OD ad DC eam habeat OE ad ER, ergo ER semper quoque major DC sive EF, et idcirco puncta R et F non possunt coincidere.
Postquam itaque vidimus pondera aequalia aequalibus internodiis ligata non pendere secundum lineam parabolicam, Quaeramus nunc quae internodiorum debeat ad invicem esse proportio, secundum quam pondera aequalia ex chorda religata secundum lineam parabolicam pendeant.
Propos. 4. Sit igitur data linea parabolica ABCDEFGa naar voetnoot9) cujus axis horizonti perpendicularis et sint nectenda ex chorda aliquâ pondera quotlibet aequalia, quae si certa ratione quadam suspendantur, puncta in quibus chordae alligata sunt, omnia sint in data linea parabolica.
| |
| |
Ducatur ζZ, quae parabolam in vertice contingat ideoque sit ad axem GC ad angulos rectos, et ponatur utcunque BC eique aequalis CD, ita ut puncta B et D sint in data parabola; dividatur porro CD bifariam in L, et parallela axi GC ducatur QLH, quae à producta BC secetur in H: fiat vero ut CH ad CB, ita HD ad DE, eaque ponatur in producta HD. DE rursus bifariam secetur in M et ducatur axi GC parallela PI, et ex I ubi illa intersecatur a producta CD, ducatur
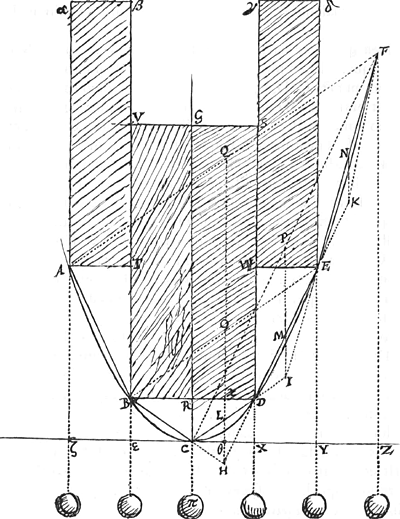
per E, linea IENF, et sit ut ID ad DC sic IE ad EF. ab altera parte axis similiter inveniatur punctum A, etc. Sic inventa puncta erunt in datâ parabolica linea; id enim simili modo probari potest, quo in 3 tia propositione probatum est punctum R in eadem linea parabolica esse in qua puncta C, D, E; haec enim simili modo quo illud inventa sunt. Si ergo per puncta A, B, C, D, E, F, chorda tendatur, et in unoquoque horum punctorum aequale pondus nectatur, et haec catena ex duobus
| |
| |
quibuslibet eorundem punctorum (sumamus A et F) suspendatur, dico praestitum esse quod postulabatur; Situm enim hunc retinebunt, cum bina quaeque internodia, puta BC et ED, intermedio relicto uno CD se intersecent in pendula duorum ponderum gravitatis diametro in HGa naar voetnoot10); et demonstratum jam est in data parabola esse.
Manifestum hinc quoque est, si aequalia pondera secundum parabolicam lineam pendeant, tunc si producantur BC, ED, fore ut HC ad CB sic HD ad DE.
Varia autem hic contemplanda occurrunt, et quidem prae caeteris notatu dignum, quod chordae FZ, EY, DX, et C[π] etc., ex quibus pondera haec dependent omnes aequalibus intervallis distant, id est, si secentur a linea ζ Z, spatia interjecta ZY, YX, XC etc. omnia esse aequalia. CH enim aequalis est CL, ergo quia sicut HC ad CB, sive ut CL ad CD, sic HD ad DE, erit quoque DE dupla DH; quia autem HD est ad D ϰ ut DE ad EW, erit etiam WE sive XY dupla ϰ D sive θ X, id est aequalis CX. Similiter de spatio ZY demonstratur quia enim ID est aequalis DL sive dimidiae DC, et est sicut CD ad DI, ita FE ad EI, erit et ideo EF dupla EI et consequenter spatium ZY aequale spatio YX. Apparet ergo hinc si puncta B C D E F sint in linea parabolica, spatia CX, XY, YZ esse aequalia; conversum autem aeque verum est, nempe si haec spatia aequalia sunt puncta B C D E F in linea parabolica esse, cum enim XY data est aequalis CX data est linea YE, et cum sit quoque data HE, data etiam est earum intersectio E, quae non potest nisi in unico puncto esse.
Hinc sequitur,Ga naar voetnoot11) quod si loco appensorum ponderum imponantur punctis A, B, C, D, E, parallelepipeda aequalia AαβT, BVGR, RGSD, WγδE ex
| |
| |
materia quâlibet, quorum alterum alterius pressionem non impediat, relinquatur autem appensum pondus π, chordam eundem situm retenturam, quem habuerat appensis ponderibus. et quantumvis extremitates chordae A, F, aperiantur, semper tamen puncta in quibus parallelepipeda haec premunt fore in linea parabolica; semper enim premetur chorda ab aequalibus ponderibus quae sita erunt ex aequalibus distantiis, ut erant ante.
Notandum quoque est, quia CX, XY, YZ sunt spatia aequalia et puncta
C, D, E, F sunt in parabola, quam ζZ contingit in vertice C, spatium DX esse 1, spactium EY, 4, spatium FZ 9, et sic porro secundum seriem consequentium quadratorum.
Praeterea notandum triangula omnia, CHD, DIE, EKF esse aequalia, singula vero triangulo CRD.
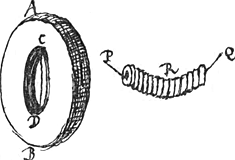
Possunt autem et cylindri sumi, qualis hic appositus est AB, in medio magno foramine CD perforatus, per quod trajicienda est chorda: Si enim quotlibet talium cylindrorum ex chorda suspendantur (chordam autem nullius ponderis esse, et cylindros mutuo contactu a pressione nihil impediri postulo) pendebunt secundum lineam parabolicam, ut videre est in cylindrulis R; quantumvis etiam extremitates chordae P, Q dilatentur vel conjungantur.
|
-
voetnoot1)
- Chr. Hugenii, etc. Exercitationes Mathematicae, Fasc. II, p. 31.
-
voetnoot2)
- La conception de cette pièce, où il est démontré ‘qu'une.... chaine pendue ne faict point une parabole, et quelle doit être la pression sur une corde... sans gravité pour en faire une’, peut être considérée comme le premier coup d'aile du génie du jeune Huygens qui avait alors l'âge de 17 ans. Quel en a été l'origine? On ne peut par le savoir avec sûreté; mais il est présumable que Huygens ait connu l'édition des ‘OEuvres Mathématiques’ de Stevin, annotée par Albert Girard, homme connu et beaucoup apprécié par Huygens, pére. Et il semble mème très probable que Huygens s'est servi de cet ouvrage, cité par nous dans la note 14 de la Lettre No. 2709 (p. 187 du Tome X), pour étudier l'‘Art pondéraire’ de Stevin comme cela lui avait été recommandé par Stampioen dans la Lettre No 5 (p. 7 du T. I). Alors il y aura rencontré l'assertion de Girard. (Voir la note 16 de la Lettre No. 2709, p. 188 du T. X) que ‘les... cordes lasches ou fort estenduës sont des lignes paraboliques’, ce dont Girard prétendait posséder la démonstration. Et Huygens se sera mis a chercher cette démonstration perdue.
Comme Huygens l'a raconté lui-même dans la pièce No. 2724 (p. 217 du T. X), sa démonstration fut examinée par Descartes et c'est donc bien probablement à elle que se rapportent les paroles de Descartes qui suivent, et qu'on trouve dans sa lettre du 15 juin 1646 à le Leu de Wilhem, oncle de Christiaan Huygens (le No. 9, p. 14 de notre T. I, publié aussi T. IV, p. 436 de l'édition d'Adam et Tannery des OEuvres de Descartes): ‘Il y a quelque tems que le Professeur Schooten m'enuoya un escrit que le second fils de Mr. de Zuylichem auoit fait touchant vne invention de Mathematique qu'il auoit cherchée, et encore qu'il n'y eust pas tout a fait trouué son conte (ce qui n'estoit nullement estrange pource qu'il auoit cherché vne chose qui n'a jamais eté trouueé de personne) il sy estoit pris de tel biais que cela m'assure qu'il deviendra excellent en cete science, en laquelle ie ne voy presque personne qui scache rien.’
Dans sa première lettre à Mersenne, du 28 octobre 1646, (voir la p. 28 du T. I) Huygens mentionna sa découverte et promit de lui en envoyer la démonstration. Mersenne, dans sa réponse, (p. 31 du T. I) l'excite à chercher de même comment une corde devrait être chargée pour faire l'hyperbole ou l'ellipse, et lui communique que Galilée, dont Huygens probablement ne connaissait pas encore les ouvrages (voir la note 15 (p. 73) de la pièce No. XIV) avait cru que la courbe de la chaîne était une parabole.
Deux mois plus tard, après un rappel que lui adressa Mersenne dans sa lettre du 8 décembre, (p. 46, T. I.), Huygens accomplit sa promesse, s'excusant du retard dans la lettre d'envoi du 23 décembre (p. 557 du T. II), en écrivant ‘quand j'ay trouué quelque chose de nouveau en Mathematiques je ne la mets pas incontinent par escrit, mais il me suffit de le pouvoir faire quand je veus, ou quand on m'en demande la demonstration: De la sorte doncques je n'avois encore rien escrit de cet affaire de la chaisne qu'une ou deux propositions.’
Ces paroles font supposer que la pièce que nous donnons a été précédée encore d'une autre d'une rédaction plus sommaire, ou plutôt que les propositions 3 et 4 ont été ajoutées après coup, supposition qui trouve quelque appui dans une raie qui traverse la page du manuscrit. Quoiqu'il en soit, l'écrit envoyé à Mersenne en différait par ce qu'il était sans doute rédigé plus savamment par ‘suppositions’ ‘propositions’ et ‘corollaires,’ comme la lettre No. 30 de Mersenne (T. 1. p. 64) le prouve et de même la pièce No. 20 (T. 1. p. 34) qui ne représente d'ailleurs qu'un projet d'une lettre qui n'a jamais été expediée sous cette forme. En effet, Huygens n'a envoyé son traité de la chaîne qu'avec la lettre du 23 décembre, comme cela résulte de cette lettre elle-même et du début du No. 23a (T. 2, p. 554).
Mersenne, après la réception du petit chef d'oeuvre, témoigne à trois reprises, dans les lettres No. 24, 25 et 30 du 3, du 8 et du 24 janvier 1647 (T. I, p. 47, 50 et 64) de son admiration croissante; toutefois dans la dernière de ces lettres, en admettant pleinement la justesse du résultat, il fait des exceptions contre la méthode de démontrer qui, d'après le témoignage de Huygens dans sa lettre du 12 juillet 1648, que nous citerons plus bas, était celle de Stevin. Ce qui implique qu'elle ne différait pas sensiblement de celle de la pièce que nous reproduisons.
Au premier abord, ces remarques de Mersenne ne semblent pas avoir beaucoup impressioné Huygens; mais lorsque, dans la lettre No. 50 du 15 mai 1648 (T. I, p. 93), Mersenne lui promit de faire imprimer le petit traité de la chaîne pourvu qu'il y ajoutât la démonstration exigée, il se remit à l'oeuvre et c'est sans doute à cette occasion qu'il redigea la pièce No. 22 (T. 1, p. 40), où la démonstration se fonde sur un tout autre principe: celui que le centre de gravité se place aussi bas que possible. Quant à la pièce No. 21 qui la précède, il est difficile de décider si elle date de cette même époque ou si elle appartient à la première rédaction qui fut envoyée à Mersenne en décembre 1646.
Ajoutons que le manuscrit de la pièce No. 22 ne s'arrête pas là où cette pièce finit dans notre T. I; mais qu'il procède jusqu'à une proposition qu'on retrouve vers la fin de la pièce No. 21 dans le dernier alinéa de la page 39. Mais cette dernière partie ne diffère pas assez de la partie correspondante de la pièce No. 21 pour qu'il soit nécessaire de la reproduire.
Ainsi, quoique nous ne connaissions pas exactement la rédaction définitive du nouveau traité qui fut préparé pour Mersenne, les pièces No. 21 et 22 lues à commencer par la dernière, nous en donnent une notion assez complète. De plus, nous avons la lettre No. 57b du 12 juillet 1648, la dernière de la correspondance avec Mersenne, qui mourut le 1er septembre de la même année. Dans cette lettre Huygens lui manda [p. 569 du Tome II] qu'il avait ‘nouvellement reveu et corrigé’, [le traité de la chaîne] ‘et augmenté de la nouvelle demonstration du premier theorème’ [la Prop. 1 de la pièce No. 22] ‘qui m'a donnè plus de peine presque que tout le reste du traitté, il a fallu 3 vel 4 lemmata’ [voir les trois lemmata de la pièce citée] ‘quae ad conica spectant devant que de le pouvoir demonstrer, et pourtant j'ai aymè mieux prendre toute ceste peine que de bailler la demonstration de Stevin’ [celle du Theorema 1mum de la pièce ici reproduite, démonstration, qui en effet n'est qu'une ampliation de celle qu'on trouve p. 57 et 58 de l'ouvrage de Stevin, cité dans la note 12 de la pièce No. 5 (T. I, p. 7)] ‘pour suffisante, car il me semble qu'elle ne l'est pas.’ Après quoi Huygens fait suivre: ‘Il ne me reste maintenant qu'à descrire mon traittè, et je vous l'envoyeray aussitost, affin que vous en disposiez comme bon vous semblera.’
-
voetnoot3)
- Voir la p. 57 de l'ouvrage de Stevin, cité dans la note 12 de la pièce No. 5 (T. I, p. 7).
-
voetnoot4)
- Dans l'écrit envoyé à Mersenne en décembre 1646 cette remarque (que le centre de gravité des poids G et H, et par suite le point A, 's approchent, dans la position de la figure autant que possible du centre de la terre), doit avoir pris la forme d'un Corollaire. Et c'était par la démonstration de ce Corollaire que Mersenne conseilla Huygens de commencer toute la ‘spéculation de la chorde.’ Voir la lettre du 24 janvier 1647, p. 64 du Tome I.
Pour subvenir à cette observation, Huygens avait à remplaçer (voir l'axiome 5 de la pièce No. 22, T. I, p. 41) les cercles que les points D et C peuvent décrire, par leurs tangentes, pour chercher ensuite le lieu du point A. Or, la solution de ce problème, qui est contenue dans le Lemina 1 de la pièce No. 22, se trouvait toute faite au Caput III, p. 14 de l'ouvrage de van Schooten de 1646, cité dans la note 2 de la Lettre No. 30 (T. I, p. 65) et sans doute le nom ‘Schoten,’ écrit en marge du manuscrit de la pièce No. 22, a quelque rapport avec cette circonstance.
Le lieu du point A une fois connu, Huygens, pour arriver à la ‘propositio I’ de la pièce No. 22, avait encore à démontrer que l'ellipse en question est coupé à angle droit par la verticale AB de la figure du texte, ce qu'il fit dans le Lemma 2 de cette pièce No. 22. Ajoutons qu'en 1688 il a repris cette démonstration, voir la note 17 de la pièce No. 2724 (T. X, p. 218).
-
voetnoot5)
- On retrouve cette proposition dans la pièce No. 21 comme Prop. 8.
-
voetnoot7)
- ‘Si in coni sectione, uel circuli circumferentia duas lineas aequidistantes recta linea bifariam secet, diameter erit sectionis.’ (voir p. 55 de l'édition de Commandin, citée T. I, p. 6, note 4.)
-
voetnoot8)
- C'est-à-dire en supposant que le point D est le point le plus bas de la chaîne.
-
voetnoot11)
- Après plus de vingt ans Huygens annota ici en marge ‘non sequitur neque est verum. 1668.’ En effet, dans la supposition qui va suivre dans le texte, il faut, en négligeant la friction, que la tension T0 de la corde soit partout la mème. On aura donc dans le cas limite
T0dy/ds = μx, d'où il suit facilement que la courbe en question doit être alors un arc de cercle, accompagné, s'il en est besoin, de deux droites verticales, et non pas une parabole. Nous ne savons pas si Huygens a connu ce résultat; mais nous pouvons indiquer avec beaucoup de probabilité quelle a été l'occasion qui lui a fait reprendre en 1668 ses recherches sur la chaîne. C'était à propos de la lecture d'un ouvrage imprimé ou, plus probablement, d'un manuscrit, d'un certain Regnault ou Regnauld. Cela résulte d'une annotation qui se trouve dans le livre des Adversaria D à un lieu qui correspond très bien à la date de 1668. Voici cette annotation:
‘Mr. Regnauld veut qu'une chaine AIgIB estant attachée par A et B, et ayant son affaisement EG’ [lisez Eg] ‘égal à la moitié de AB, se courbe suivant AIgIB qu'il décrit en faisant le ▭ ACDB, et mettant FI proportionelle aux lignes GF, HF, AHGHB’ [lisez AHgHB] ‘estant un demi cercle. le probleme que Mr. Regnault propose est assurement des plus difficiles à resoudre, Et quant à la solution qu'il en donne j'y trouve ces deux choses à dire.
Premierement que sa demonstration ne prouve nullement ce qui est proposé, la considération du levier ni du momentum ponderis n'y estant pas bien prise, et encore moins celle des espaces parcourus par le mouvement acceleré.
Secondement que sa courbe AIg IB, suivant la construction qu'il en donne n'est autre chose qu'une parabole dont le paramètre est Eg, quoy qu'il pense avoir demonstré le contraire.’
Après 1668 Huygens semble avoir laissé tomber complètement le sujet jusqu'à la date mémorable où Jean Bernoulli proposa aux géomètres dans les ‘Acta’ du mois de mai 1690 le problème de la chaînette. Voir la correspondance de 1690-1693, T. IX et X de notre publication.
|








