Logo DBNL
Oeuvres complètes. Tome XII. Travaux de mathématiques pures 1652-1656 (1910)

Oeuvres complètes. Tome XII. Travaux de mathématiques pures 1652-1656

(1910)–Christiaan Huygens–rechtenstatus Auteursrecht onbekend

Vorige Volgende

Ad C.V. Fran. Xaver. Ainscom, S.I. epistola.
1656.

Avertissement.

En composant son ‘Ἐξέτασις Cyclometriae Cl. Viri Gregorii à S. Vincentio’1), Huygens avait espéré de pouvoir, par la lucidité de son exposition et la force de ses arguments, convaincre Grégoire lui-même de l'insuffisance de sa quadrature du cercle2).

Après la publication, en décembre 1651, il fut bientôt désappointé par l'attitude évasive de Grégoire, qui, nonobstant les insistances de plus et plus pressantes de Huygens, persista à réserver son jugement jusqu' au jour où il répondrait à tous ses adversaires à la fois3). Un moment alors Huygens se trouva sur le point de perdre patience. Ce fut lorsque dans le brouillon d'une de ses lettres à Grégoire il lui adressa, entre autres, l'allocution célèbre de Cicéron ‘Quousque tandem abuteris patientia nostra!’4). Mais il se reprend et se contente dans la lettre qu'il

écrit de prier Grégoire emphatiquement de vouloir du moins lui indiquer en trois mots ‘combien de fois le rapport 53 à 203 contient le rapport 5 à 11 dans le sens de sa 44ième Proposition du Livre 10’5).

C'est en effet de la réponse à donner à cette question que dépend la réduction à l'absurde qui constitue la partie principale de l'‘Ἐξέτασις’6). Une réponse numérique aurait permis de calculer, en admettant la justesse de la quadrature de Grégoire, la valeur du rapport de la circonférence du cercle au diamètre et d'en démontrer la discordance avec la valeur approchée bien connue de ce rapport. Au lieu de cela Grégoire renvoie7) à un ouvrage d'un de ses élèves, le père de Sarasa8), d'où il suit, en effet, que le sens que Grégoire veut donner à l'expression ‘contenir’ se trouve étre celui même que nous avons suggéré dans la note 28 de la page 280 du Tome XI et d'après lequel le nombre de fois que le premier rapport ‘contient’ le second est exprimé par la valeur de n dans l'équation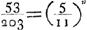 illustratie. La réponse ne manquait donc pas de précision comme on serait tenté de le croire au premier abord; mais elle impliquait que, même en admettant la justesse de toutes les propositions qui avaient amené la première de ses quadratures prétendues, Grégoire n'avait pas donné la quadrature proprement dite du cercle mais seulement la réduction de cette quadrature à celle de l'hyperbole ou aux logarithmes.

Trois mois plus tard, en juillet 1652, Huygens avait à Gand un entretien amical avec Grégoire qui lui laissa entendre que son livre avait été rédigé par ses élèves, qu'il se pourrait bien qu'une erreur se fût glissée dans la première quadrature, la seule attaquée directement par Huygens; mais qu'il avait confiance dans les autres. En quittant Grégoire, Huygens était sous l'impression que la réponse tarderait encore longtemps à paraître et qu'elle ne vaudrait pas grand' chose9).

Toutefois, déjà en janvier 1653 Huygens apprit10) qu' une réfutation de son ‘Ἐξέτασις’ était prête, composée par un des élèves de Grégoire, le père Aynscom. Elle ne parut qu'en 165611). En attendant, Kinner à Löwenthurn, un

autre élève, prit la défense de son ancien maître. Dans ses lettres à Huygens du 30 novembre 1652 et du 18 juillet de l'année suivante12) il contesta que la première quadrature de Grégoire fût celle à laquelle l'auteur avait donné la préférence sur les autres, comme Huygens l'avait prétendu13). Tout au contraire il considérait qu' avec elle l'auteur avait plutôt voulu montrer la possibilité de la quadrature du cercle que de l'exposer de fait. C'était la seconde quadrature qui, d'après l'opinion de Grégoire lui-même, était la plus facile. Lui, Kinner, l'avait rédigée en 35 propositions qu'il publierait peut-être bientôt; ce qu' il fit en effet dans son ouvrage ‘Elucidatio geometrica Problematis Austriaci sive Quadratura Circuli feliciter tandem detectae per R.P. Gregorium a S. Vincentio’14).

Aussitôt après la réception de cette ‘Elucidatio’ Huygens chercha à détromper Kinner en lui indiquant le lieu précis où il avait trouvé sa quadrature en défaut15); mais il ne réussit pas à le convaincre16).

Après ce premier passe d'armes avec un des élèves de Grégoire, Huygens avait encore à attendre plus de deux années avant qu'il reçut, en juillet 1656, la réponse du père Aynscom17), annoncée depuis si longtemps. Dans cet ouvrage de 182 pages in folio, l'auteur s'efforce à réfuter tous les adversaires des quadratures de Grégoire. Il les divise en deux classes: ceux qui ont attaqué les théorèmes sur les proportionnalités et ceux qui, laissant de côté ces théorèmes ou admettant leur justesse, se sont occupés des propositions dont les quadratures dépendent plus directement. Après avoir rendu hommage dans sa préface aux adversaires, parmi lesquels il donne au jeune Huygens la première place, qui se sont servis de méthodes dignes de géomètres, quoiqu' ils n'aient pas atteint leur but18), il répond à ceux de la première classe par son ‘Liber primus’, qui occupe les 88 premières pages de son ouvrage. Puis le second livre débute, dans sa ‘Pars prima,’ par un résumé de la première quadrature de Grégoire avec des explications authentiques suivant les intentions de son auteur19); tandis que la ‘Pars secunda’ prend à tâche de réfuter l'un après l'autre tous les adversaires de la ‘seconde classe’ par autant de ‘Responsiones’20), desquelles nous reproduisons

plus loin21) la ‘Responsio III ad Ἐξέτασιν Clariss. D. Christiani Hugenij’. Enfin Aynscom conclut par un troisième, quatrième et cinquième Livre qui contiennent des exposés des trois autres quadratures de Grégoire.

Inutile de dire que le père Aynscom ne réussit pas à sauver ni la première quadrature, ni les autres; toutefois une chose ressort très nettement de son exposition. Nous voulons parler de l'emploi, par Grégoire, du terme ‘contenir’ dans la ‘Demonstratio’ de sa 44e proposition du ‘Lib. 10’, proposition dont dépend sa première quadrature. Quel est le sens de ce terme dans la phrase ‘qu'un rapport donné en contient un autre un certain nombre de fois’? Huygens, dans son ‘Ἐξέτασις’22), examine successivement deux interprétations diverses. Il en rejette la première, celle que nous venons d'exposer plus haut, en remarquant que le rapport 53 à 203 n'est du rapport 5 à 11 ni le carré, ni la troisième puissance ou quelque puissance plus élevée’, ensuite il en hasarde avec beaucoup de réserve une autre qui amène la réduction à l'absurde qu'il fait suivre. Or, il n'y a aucun doute que cette première interprétation était celle, visée par Grégoire23). La circonstance alléguée par Huygens que le nombre n qui doit satisfaire à la relation 53/203=(5/11)n est nécessairement un nombre incommensurable n'y fait pas obstacle, puisque la ‘Prop. 129’24) du ‘Lib. 6’ de l'ouvrage de Grégoire, citée par

Aynscom25), équivant pleinement à l'introduction des exposants incommensurables. Toutefois elle change entièrement la portée de la prétendue quadrature, qui, comme nous l'avons déjà remarqué, ne donnerait autre chose que la réduction de la quadrature du cercle à la détermination d'un nombre qui n'est exprimable qu' à l'aide des logarithmes26). Sous ce point de vue Huygens a raison de rejeter cette première interprétation comme ne menant pas à une quadrature proprement dite.

Dès que Huygens eut reçu l'ouvrage d'Aynscom il prépara sa réplique. Il l'annonce à De Roberval27) et à Wallis28) duquel il se propose de citer dans cette réplique l'opinion, conforme à la sienne, exprimée par Wallis dans la préface de son ‘Arithmetica Infinitorum’. Le 25 septembre il envoie le manuscrit à l'imprimeur Elsevier29). Au commencement d'octobre 1656 l'impression est achevée30).

Aynscom, qui reçut un exemplaire par l'intermédiaire du père Seghers31), n'a jamais répondu, nonobstant un rappel que Huygens lui fit parvenir en 1659 par le mème père32).

Ainsi la poussière soulevée par la quadrature du cercle de Grégoire St. Vincent, les attaques de Mersenne33), Sylvius34), Maybaum35), Léotaud36), Auzout37) et Huygens et les réponses de de Sarasa, Kinner à Löwenthurn et Aynscom, retombait enfin au repos, et toute cette polémique, qui a occupé le monde savant pendant plus de dix années, aurait laissé bien peu de traces, ne fût-ce que tout ce qui regarde un homme comme Huygens ne cessera jamais d'inspirer un certain intérêt.


Vorige Volgende