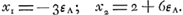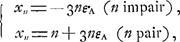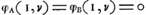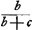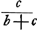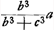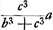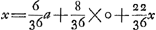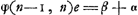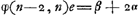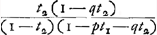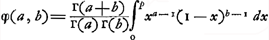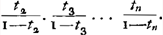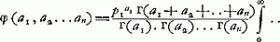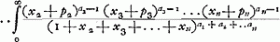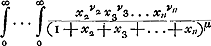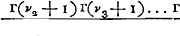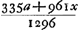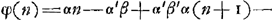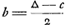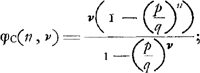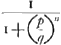Oeuvres complètes. Tome XIV. Probabilités. Travaux de mathématiques pures 1655-1666
(1920)–Christiaan Huygens–
[pagina 1]
| |||||||||||||||||||||||||||||||||||||||||
Van rekeningh in spelen van geluck.
| |||||||||||||||||||||||||||||||||||||||||
[pagina 3]
| |||||||||||||||||||||||||||||||||||||||||
Avertissement.Aperçu de la genèse de l'ouvrage ‘De ratiociniis in ludo aleae’ et des recherches subséquentes de Huygens sur des questions de probabilité.On sait qu'en 1654 le Chevalier de Méré, joueur renommé et un peu mathématicien, proposa à Pascal quelques problèmes concernant les jeux de hasardGa naar voetnoot1), qu'il en résultait un échange de lettresGa naar voetnoot2) entre Pascal et Fermat et que ce fut là l'origine du calcul des probabilités. Or, l'année suivante, le jeune HuygensGa naar voetnoot3), déja connu par quelques ouvrages de mathématiquesGa naar voetnoot4), se rendit à Paris en compagnie de son frère Louis et de son cousin DoubletGa naar voetnoot5). Ce séjour, jugé alors nécessaire pour compléter l'éducation de gentilshommes hollandais de leur conditionGa naar voetnoot6), se prolongea de la mi-juillet jusqu'à la fin de novembre. Huygens ne | |||||||||||||||||||||||||||||||||||||||||
[pagina 4]
| |||||||||||||||||||||||||||||||||||||||||
rencontra à cette occasion ni Fermat (qui demeurait à Toulouse), ni PascalGa naar voetnoot1), ni CarcavyGa naar voetnoot2) qui avait servi d'intermédiaire lors de l'échange de lettres de ces deux savants sur les problèmes de de MéréGa naar voetnoot3); mais il fréquenta Claude Mylon, un des amis de CarcavyGa naar voetnoot4), et Roberval à qui l'on s'était adressé, de même qu'à Pascal, pour la solution des problèmes qui occupaient de MéréGa naar voetnoot5). Il n'y a donc pas lieu de s'étonner que Huygens fut informé de l'existence de ces problèmes (dont l'un est resté connu sous le nom de ‘problème des partis’ et dont nous appellerons les autres ‘les problèmes des dés’) sans avoir l'occasion d'en connaître les solutions obtenues par Pascal et Fermat, ou les méthodes suivies par eux. De retour en Hollande, Huygens ne tarda pas à commencer la composition de son Traité du calcul dans les jeux de hasard, qui roule presqu'entièrement sur les problèmes prémentionnés. Déja en mars 1656, il put écrire au professeur van Schooten qu'il lui enverrait ce qu'il préparait sur les jeux de désGa naar voetnoot6); le 18 avril il fit savoir à RobervalGa naar voetnoot7) qu'il avait ‘depuis quelques jours escrit les fondements du calcul es jeux de hasard à la priere de Monsieur Schooten qui le veut faire imprimer’, et il lui posa le problème qu'on trouve dans la XIVième PropositionGa naar voetnoot8) de son Traité, en ajoutant qu'il désirait fort voir si lui (Roberval) en trouverait | |||||||||||||||||||||||||||||||||||||||||
[pagina 5]
| |||||||||||||||||||||||||||||||||||||||||
la même solution. Enfin, le 20 avril, il envoya à van Schooten un manuscrit qui probablement ne différait du texte que nous publions que par l'absence de la Prop. IXGa naar voetnoot9) et des Exercices vers la fin du Traité, dont Huygens abandonne l'analyse à ses lecteursGa naar voetnoot10). Il fut donc convenu entre van Schooten et lui que le petit traité de Huygens serait inséré dans l'ouvrage ‘Exercitationum mathematicarum Libri quinqueGa naar voetnoot11)’ dont van Schooten préparait la publication. Cet ouvrage paraîtrait en deux éditions, l'une latine, l'autre hollandaiseGa naar voetnoot12). L'édition latine devant être publiée la première, il était nécessaire de se procurer d'abord une version latine du manuscrit de Huygens que celui-ci avait écrit en hollandais parce que les termes latins lui manquaient. Après avoir achevé son ouvrage, il trouva cependant plusieurs de ces termesGa naar voetnoot13). Par suite il se fit fort, si c'était nécessaire, d'élaborer une traduction latine; mais avant de s'y consacrer il voulut savoir si van Schooten approuvait la manière dont il avait traité son sujetGa naar voetnoot14). Celui-ci lui répondit qu'il ferait la traduction lui-même, mais le pria de lui envoyer tout ce qui pouvait faciliter cette tâcheGa naar voetnoot15). C'est à cette circonstance que nous devons la Pièce No. 289, p. 414-416 du T. I, qui nous fait connaître la disposition | |||||||||||||||||||||||||||||||||||||||||
[pagina 6]
| |||||||||||||||||||||||||||||||||||||||||
générale du Manuscrit envoyé, le 20 avril, à van Schooten. Lorsqu'on compare les phrases latines, suggérées par Huygens dans cette Pièce, avec le texte latin, tel qu'il parut dans les ‘Exercitationes’, on peut constater que, dans sa traduction, van Schooten n'a fait qu'un usage limité des indications de Huygens. Ajoutons que celui-ci n'était pas tout-à-fait satisfait de cette traductionGa naar voetnoot1); ce qui fut pour nous une raison de plus de préférer pour notre texte la version hollandaise à la version latine, quoique cette dernière eût paru trois années plus tôt que l'autre. En attendant la publication de son Traité, qui n'eut lieu que l'année suivante, Huygens devint de plus en plus anxieux de savoir si ses solutions et sa méthode s'accordaient avec celles des mathématiciens français. Ne recevant aucune réponse à sa lettre du 18 avrilGa naar voetnoot2) à Roberval, il s'adressa à Mylon pour lui poser le même problème ainsi que quelques autres plus simplesGa naar voetnoot3). Les solutions, en partie faussesGa naar voetnoot4), que Mylon lui envoya ne peuvent avoir eu beaucoup d'intérêt pour lui; mais c'est à cette occasion que, par l'intermédiaire de Mylon et de Carcavy, le problème principal parvint à la connaissance de Fermat et de PascalGa naar voetnoot5). En effet, le 22 juin 1656Ga naar voetnoot6) Carcavy fit part à Huygens de la solution de Fermat de ce problème, laquelle se trouvait être conforme à celle de Huygens. De plus, Fermat posa à Huygens d'autres questions plus dissicilesGa naar voetnoot7). Or, le même après-midi qu'il les reçoit, Huygens ‘trouve la solution de toutes, quant à la methode, non pas quant au calcul; qui est si long dans quelques unes d'elles qu'[il n'a] pas voulu s'amuser à le poursuivre jusques au boutGa naar voetnoot8)’. | |||||||||||||||||||||||||||||||||||||||||
[pagina 7]
| |||||||||||||||||||||||||||||||||||||||||
On trouvera le résultat des recherches de cet après-midi dans la lettre de Huygens à Carcavy du 6 juillet 1656Ga naar voetnoot9), laquelle était destinée à être communiquée à Mylon, à Fermat et à PascalGa naar voetnoot10) afin de savoir si ce que ces deux derniers avaient trouvé était conforme à ‘ce qu'[il] en explique’ dans cette lettre. Outre les solutions des problèmes prémentionnés, la lettre contient la Prop. III (p. 65), sur laquelle toutes ces solutions étaient fondées. La réponse de Carcavy se fit longtemps et impatiemmentGa naar voetnoot11) attendre. Quand elle arriva, au commencement d'octobreGa naar voetnoot12), elle apprit à Huygens que Pascal se servait de la même propositionGa naar voetnoot13) que lui mais qu'il ne voyait pas de quelle manière celle-ci pourrait s'appliquer au problème des partisGa naar voetnoot14) dont ‘le sieur Pascal n'a trouué la reigle que lors qu'un des joueurs a une partie à point, ou quand il en a deux à point’. C'est sans doute par suite de cette remarqueGa naar voetnoot15) que Huygens reprit ses recherches sur ce dernier problème et qu'il écrivit, d'abord | |||||||||||||||||||||||||||||||||||||||||
[pagina 8]
| |||||||||||||||||||||||||||||||||||||||||
l'Appendice I (p. 92-95), destiné probablement à être communiqué à PascalGa naar voetnoot1), et ensuite la Prop. IX (p. 73-77) qu'il allait joindre au petit traité qu'il avait composéGa naar voetnoot2). Cependant on continua avec la lenteur habituelle de ces temps l'impression de l'ouvrage de van Schooten où le traité de Huygens est inséré. En mars 1657 van Schooten avertit Huygens que dans quelques semaines on en serait à ce traité. Il lui envoia donc le manuscrit de la traduction latine pour y ajouter ce que bon lui sembleraitGa naar voetnoot3). Huygens le lui retournaGa naar voetnoot4) avec quelques changements et quelques additionsGa naar voetnoot5), en y joignant la version latine de sa lettre à van SchootenGa naar voetnoot6), datée du 27 avril 1657, qui précède son Traité en guise de préface. Enfin, en août ou septembre 1657, l'impression de l'édition latine de l'ouvrage de van Schooten fut achevéeGa naar voetnoot7). L'édition hollandaise se fit attendre encore trois années, mais il nous semble inutile d'exposer ici les raisons de ce retardGa naar voetnoot8).
Avant de passer à d'autres sujets nous voulons ajouter encore quelques mots sur l'historique du Traité ‘De ratiociniis in ludo aleae’ après sa publication en 1657. Comme on le sait, plusieurs des oeuvres les plus considérables de Huygens ne parurent que longtemps après leur première rédactionGa naar voetnoot9); ce qui lui coûta la | |||||||||||||||||||||||||||||||||||||||||
[pagina 9]
| |||||||||||||||||||||||||||||||||||||||||
priorité sur bien des points importants. Grâce à van Schooten - on doit le reconnaître - la publication du petit traité sur les probabilités ne fut pas différée. L'ouvrage fut accueilli favorablement par les contemporainsGa naar voetnoot10). Pendant plus d'un demi-siècle (c'est-à-dire jusqu'à la publication des ouvrages de de MonmortGa naar voetnoot11), de de MoivreGa naar voetnoot12), de Jacques BernoulliGa naar voetnoot13) et de Nicolaas StruyckGa naar voetnoot14), il forma l'unique introduction existant à la théorie des probabilités. Dans cet intervalle, ou peu après, deux traductions anglaises en parurentGa naar voetnoot15). Enfin, Jacques | |||||||||||||||||||||||||||||||||||||||||
[pagina 10]
| |||||||||||||||||||||||||||||||||||||||||
Bernoulli, en composant son ‘Ars conjectandi’, y inséra en entier le Traité de Huygens comme ‘Pars prima, complectens Tractatum Hugenii de Ratiociniis in Ludo Aleae, cum Annotationibus Jacobi Bernoulli’Ga naar voetnoot1).
En 1665, à l'occasion d'une lettre de son ami Johan Hudde, le futur bourgmestre d'AmsterdamGa naar voetnoot2), l'attention de Huygens fut dirigée à nouveau sur les problèmes concernant les jeux de hasard. Dans cette lettreGa naar voetnoot3) Hudde lui communiqua ses solutions des Exercices II et IV, proposés par Huygens vers la fin de son TraitéGa naar voetnoot4). En cherchant lui-même leurs solutionsGa naar voetnoot5), Huygens en trouva qui différaient de celles de Hudde; ce qu'il lui fit savoir dans sa réponse du 4 avril 1665Ga naar voetnoot6). En même temps, il lui posa une nouvelle question, savoir: de déterminer le désavantage du joueur qui fait le premier coup quand deux joueurs jettent à tour de rôle croix ou pile à condition que celui qui amène pile doit mettre chaque fois un ducat et que celui qui jette croix prendra tout ce qui est mis. | |||||||||||||||||||||||||||||||||||||||||
[pagina 11]
| |||||||||||||||||||||||||||||||||||||||||
Cette question fit naître toute une série de problèmes touchant l'avantage ou désavantage de la primauté sous des conditions variées. Plus bas nous traitons ces problèmes avec quelque détailGa naar voetnoot7). Quant à la divergence des solutions des Exercices II et IV, elle parut être due aux interprétations différentes données par Hudde et Huygens à ces Excercices. Comme nous le montrons dans la note 3 de la p. 88, l'Exercice II n'admet pas moins de trois interprétations, dont la première fut adoptée par HuygensGa naar voetnoot8) et la deuxième par HuddeGa naar voetnoot9). De même l'Exercice IV donne lieu à deux conceptions dont l'une, conduisant au résultat des §§ 2 et 3 de l'Appendice IIGa naar voetnoot10), fut choisie par Huygens, et l'autre, aboutissant au résultat du § 4 du même AppendiceGa naar voetnoot11), fut admise par HuddeGa naar voetnoot12). En effet, les solutions de Hudde de ces problèmes étaient correctes (à part une légère erreur de calcul), et il en est de même de ses solutions d'autres problèmes qu'on rencontre dans sa correspondance avec HuygensGa naar voetnoot13). Plus on étudie ses longues lettres, par trop prolixes et difficiles à comprendre àcause des malentendus continuels qui s'élèvent entre lui et Huygens, plus on s'aperçoit de la perspicacité de leur auteur. Quant aux méthodes dont il se sert, il ne les expose qu'exceptionnellement et encore en partie seulementGa naar voetnoot14), mais les indications qu'il donne suffisent pour conclure qu'elles ne différaient pas beaucoup de celles de HuygensGa naar voetnoot15). | |||||||||||||||||||||||||||||||||||||||||
[pagina 12]
| |||||||||||||||||||||||||||||||||||||||||
Nous avons à parler ensuite, en suivant l'ordre chronologique, de quelques applications de la théorie de la probabilité à des problèmes concernant la durée de la vie. Déjà en 1662, Moray avait fait parvenir à HuygensGa naar voetnoot1) l'ouvrage de John Graunt ‘Natural and political observations.., made upon the Bills of Mortality’Ga naar voetnoot2), qui venait de paraître. Huygens avait beaucoup apprécié cet ouvrage, mais il ne s'occupa activement des matières qu'on y trouve traitées qu'au moment où il reçut, de son frère puîné Lodewijk, une lettre, datée du 22 août 1669, dans laquelle celui-ci l'informaitGa naar voetnoot3) de ce qu'il avait ‘fait une Table ces jours passez du temps qu'il reste à vivre à des personnes de toute sorte d'aage. C'est une consequence’ dit-il ‘que j'aij tiré de cette table du livre Anglois of the Bils of mortalitij, de la quelle je vous envoije icij une copie, afin que vous preniez la peine de faire un peu les mesmes supputations, et que nous puissions voir comme nos calculs s'accorderont’. Or, cette copie, qu'on trouve à la p. 519 du T. VI, donne pour chaque centaine de nouveaux-nés le nombre des survivants à l'âge de 6, 16, 26 ans, et ainsi de suite, avec des intervalles de dix années. Dans sa réponse à Lodewijk, Christiaan lui fait remarquerGa naar voetnoot4) ‘qu'a fin que ce calcul fust exact il faudroit avoir une table qui marquast d'année en année combien il meurt des personnes de 100 qu'on suppose, et’ poursuit-il ‘il faut que vous l'ayez supléée par quelque moyen comme j'en scay pour celaGa naar voetnoot5), ou autrement vous ne scauriez determiner au vray, combien doibt vivre une personne de 6, 16 ou 26 ans &c., et encore moins de quelque aage moyen entre ceux la. comme vous l'avez entrepris de vous et de moy. Je crois donc que vous n'en decidez qu'a peu pres’ et il ajoute encore ‘j'ay envie de suppleer la table comme | |||||||||||||||||||||||||||||||||||||||||
[pagina 13]
| |||||||||||||||||||||||||||||||||||||||||
j'ay dit et resoudre les problemes qu'on peut proposer en cette matiere qui est assez subtile. Vostre methode ne scauroit estre la mesme que la mienne, et je seray bien aise de la voir’. Une lettre du 30 octobre 1669Ga naar voetnoot6) nous fait connaître la méthode suivie par Lodewijk. Il a suppléé aux lacunes de la table de Graunt en supposant la mortalité constante dans chaque intervalle de dix années. Partant de cette supposition il a calculé d'une manière parfaitement exacte ce qu'on appelle aujourd'hui la ‘vie moyenne’ des personnes qui ont atteint l'âge donné. Toutefois, comme cela résulte de la même lettre, Lodewijk ne s'était pas suffisamment rendu compte de la différence qui existe entre la vie moyenne et la vie probable; différence que Christiaan lui expliqua dans sa lettre du 21 novembreGa naar voetnoot7). En même temps il promit de lui envoyer une autre fois ‘la ligne de vieGa naar voetnoot8) avec la pratique d'icelle et mesme une table des vies a chasque aage d'année en année, qui ne me coustera guere’Ga naar voetnoot9). C'est à propos de la même lettre de Lodewijk du 30 octobre que Christiaan composa la Pièce importante (p. 526-531 du T. VI) qu'il a intitulée: ‘En examinant le calcul de mon frere Louis.’ Il y met par écrit, au courant de la plume, les idées qui lui viennent pendant et après cet examen. Entre autres, il s'y pose les problèmes suivants (dans lesquels il s'agit toujours de la durée moyenne des temps mentionnés): ‘Un homme de 56 ans espouse une femme de 16 ans, combien peuvent ils faire estat de vivre ensemble sans que l'un ni l'autre meure. Ou bien si on m'avoit promis 100 francs au bout de chasque an qu'ils vivront ensemble, pour combien seroit il juste qu'on rachetast cette obligationGa naar voetnoot10). Item dans combien de temps doivent ils mourir tous deux. En combien de temps | |||||||||||||||||||||||||||||||||||||||||
[pagina 14]
| |||||||||||||||||||||||||||||||||||||||||
mourront 40 hommes de 46 ans chacun? Combien vivra le dernier de 2 personnes de 16 ans. Dans combien de temps mourra un de 2 personnes de 16 ans’. De ces problèmes assez compliqués Huygens ne résout que l'avant-dernierGa naar voetnoot1), le manuscrit s'arrêtant au milieu du calcul qui doit servir à la solution du dernier. Toutefois, il est clair que la méthode ingénieuse qu'il applique à ces deux problèmes aurait pu conduire, après quelques modifications évidentes, à la solution des autresGa naar voetnoot2).
Il est vrai que Huygens a été consulté par Hudde, en 1671, sur la méthode suivie par le célèbre Pensionnaire de Hollande et de West-Frise, Johan de Witt, dans ses calculs sur la valeur des rentes viagères que les États de Hollande se proposaient de négocierGa naar voetnoot3). Cependant, la Correspondance de Huygens de cette année nous apprend qu'il n'a pas pris une part active dans cette entre- | |||||||||||||||||||||||||||||||||||||||||
[pagina 15]
| |||||||||||||||||||||||||||||||||||||||||
priseGa naar voetnoot4). Dans sa lettre du 3 octobreGa naar voetnoot5), datée de Paris, il s'excuse auprès de Hudde de n'avoir pu trouver plus tôt le loisir de réfléchir aux calculs des rentes viagères à cause des affaires qu'il a sur les bras, et de ne pouvoir répondre à toutes les questions qu'il lui a posées. Il se borne donc à approuver d'une façon générale les méthodes suivies par le Pensionnaire, en y comprenant notamment celle qui concerne le calcul sur 2, 3 ou plus de viesGa naar voetnoot6).
En 1676, Huygens fut ramené à la considération de quelques problèmes du jeu par une communication de son ami DierkensGa naar voetnoot7). Il paraît que celui-ci s'était occupé à chercher la solution de l'un des Exercices proposés par Huygens vers la fin de son TraitéGa naar voetnoot8) et qu'il n'y avait pas réussi entièrementGa naar voetnoot9). C'est probablement à cette même occasion que Huygens composa l'Appendice VI (p. 151-155), daté d'août 1676, où il reprend et généralise la solution du dernier de ces Exercices; solution qu'il ajouta à l'énoncé du problème sans | |||||||||||||||||||||||||||||||||||||||||
[pagina 16]
| |||||||||||||||||||||||||||||||||||||||||
faire connaître l'analyse qui l'avait amenée. Pendant la même année, il examina la solution que Dierkens lui avait envoyée d'un problème concernant le jeu de quinquenoveGa naar voetnoot1). De plus Huygens élabora pour Dierkens les solutions, à l'aide des logarithmes, de quelques ‘problèmes des dés’Ga naar voetnoot2). Si dans la Prop. XIGa naar voetnoot3) de son Traité il s'est borné à déterminer en combien de fois on peut accepter avec avantage de jeter deux six avec deux dés, l'emploi des logarithmes lui permet maintenant d'étendre ses recherches aux problèmes analogues pour trois et quatre désGa naar voetnoot4).
Pendant son dernier séjour à Paris, de 1678-1681, l'attention de Huygens fut attirée sur le calcul des chances dans le jeu de la BassetteGa naar voetnoot5) alors très en vogue dans cette villeGa naar voetnoot6). En négligeant une des complications de ce jeuGa naar voetnoot7), il calcula dans | |||||||||||||||||||||||||||||||||||||||||
[pagina 17]
| |||||||||||||||||||||||||||||||||||||||||
l'Appendice VIIIGa naar voetnoot8) l'avantage du banquier sur les autres joueurs dans les différents cas qui peuvent se présenter pendant le jeu. Une solution plus complète fut donnée, sans analyse ni démonstration, par SauveurGa naar voetnoot9) dans le Journal des Sçavans du 13 février 1679Ga naar voetnoot10). Pour les cas traités par Huygens les deux solutions sont identiques entre elles et à celle publiée plus tard, en 1713, dans l'‘Ars conjectandi’ de Jacques BernoulliGa naar voetnoot11), mais il paraît que Huygens ne connaissait pas l'article de Sauveur lorsqu'il fit ses calculsGa naar voetnoot12). En outre, de MonmortGa naar voetnoot13), Jean BernoulliGa naar voetnoot14), frère de Jacques, et leur neveu Nicolas BernoulliGa naar voetnoot15), de MoivreGa naar voetnoot16) et StruyckGa naar voetnoot17) se sont occupés des chances du banquier dans ce même jeu de la Bassette, mais les cas qu'ils ont traités sont différents de ceux supposés par Huygens.
Enfin, en 1688, nous ignorons à quelle occasion, Huygens s'occupa pour la dernière fois de quelques problèmes de jeu. On en trouve les énoncés aux pp. 169, 172, 173 et 178 de l'Appendice IX. Dans les deux premiers paragraphes (p. 169-173) de cet Appendice on voit échouer ses premières tentatives de résoudre le problème qu'il s'y pose. Au § 3, p. 173-175, il simplifie le problème et il réussit facilement à le résoudre sous cette nouvelle forme. Au § 4 (p. 176) il reprend le problème principal, qu'il réduit à | |||||||||||||||||||||||||||||||||||||||||
[pagina 18]
| |||||||||||||||||||||||||||||||||||||||||
la sommation d'une suite infinie. Cette suite est de la même nature que celles dont Huygens avait trouvé les sommes en 1665 lors de sa Correspondance avec HuddeGa naar voetnoot1). Cependant il n'a pas achevé la solution du problème, du moins dans les manuscrits que nous connaissons, mais il est facile d'arriver à sa solution exacte par la voie suivie par Huygens en effectuant, après y avoir appliqué quelques corrections indiquées par lui-même, la sommation de la suite à laquelle il s'est arrêtéGa naar voetnoot2). Enfin dans le dernier paragraphe de l'Appendice la solution d'un problème analogue est interrompue également après avoir été réduite à la sommation d'une suite infinie du même genreGa naar voetnoot3). Ajoutons que dans le deuxième alinéa de la note 2 de la p. 179 nous avons donné une solution générale qui s'applique à tous les problèmes dont il est question dans l'Appendice IX. | |||||||||||||||||||||||||||||||||||||||||
Point de départ de Huygens. Son théorème fondamental. Sa méthode de résolution des problèmes du calcul des probabilités, suivie exclusivement jusque dans ses dernières recherches.Le calcul des probabilités est une science de mathématiques appliquées. Afin de pouvoir traiter une telle science sous la forme que Huygens choississait de préférence dans ses premiers ouvrages, il fallait donc commencer, à l'exemple d'ArchimèdeGa naar voetnoot4), par formuler, comme supplément aux postulats purement mathématiques, une on plusieurs hypothèses pouvant servir de point de départ à la démonstration des théorèmes dont on avait besoin. | |||||||||||||||||||||||||||||||||||||||||
[pagina 19]
| |||||||||||||||||||||||||||||||||||||||||
Ce point de départ, Huygens devait le chercher lui-même; bien qu'il ne fût pas l'inventeur du calcul qu'il allait exposer. En effet, les ‘savants français’ qui l'avaient précédé sur ce terrain ‘quoiqu'ils se missent à l'épreuve l'un l'autre en se proposant beaucoup de questions difficiles à résoudre’ avaient ‘cependant caché leurs méthodes’Ga naar voetnoot5). L'hypothèse à laquelle il s'arrêta est, en effet, un modèle de clarté et d'évidence. Il l'exprime ainsi: ‘dans un jeu la chance qu'on a de gagner quelque chose a une valeur telle que si l'on possède cette valeur on peut se procurer la même chance par un jeu équitable’Ga naar voetnoot6). À l'aide de cette hypothèse, il démontre par un raisonnement ingénieux les Propositions I, II et IIIGa naar voetnoot7) qui sont des cas particuliers du Théorème: Avoir p1 chances d'obtenir a1, p2 d'obtenir a2, etc. vaut Σpa/ΣpGa naar voetnoot8). Après avoir formulé ces Propositions, il passe immédiatement au problème des partis et aux autres problèmes qu'il se propose de résoudre. En effet, la seule méthode suivie par Huygens non seulement dans son Traité de 1657, mais aussi dans ses recherches ultérieures sur le calcul des probabilités, consiste dans une application continuelle, répétée autant de fois que le problème l'exige, de ces Propositions. Il emploie partout cette méthode, à l'exclusion de celle qui apprend à dresser, dès l'abord, à l'aide de l'analyse combinatoire, le bilan des cas favorables et défavorables à l'évènement en question. Il l'applique même dans les cas où cette derniere méthode mènerait bien plus facilement au but. | |||||||||||||||||||||||||||||||||||||||||
[pagina 20]
| |||||||||||||||||||||||||||||||||||||||||
Prenons, par exemple, le quatrième des Exercices du Traité de Huygens (p. 89). Le nombre total des permutations des 12 jetons du problème, dont 4 blancs et 8 noirs, est égal à 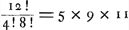 . Supposons que A, le premier des deux joueurs, en prenne toujours les sept premiers; le nombre des permutations qui lui sont favorables est alors évidemment égal à . Supposons que A, le premier des deux joueurs, en prenne toujours les sept premiers; le nombre des permutations qui lui sont favorables est alors évidemment égal à 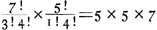 , sa chance est donc réprésentée par 35/99 et celle de l'autre joueur B par 64/99. , sa chance est donc réprésentée par 35/99 et celle de l'autre joueur B par 64/99.
Que l'on compare cette solution à celles du même problème que Huygens a données en 1665, telles qu'on les trouve aux § 2-4 de l'Appendice II, p. 97-99 du présent Tome. Évidemment il était facile à ses successeurs immédiats: de Monmort, de Moivre, Bernoulli et StruyckGa naar voetnoot1) de dépasser sur plusieurs points importants l'oeuvre de Huygens, au moyen de l'application de l'analyse combinatoire. Et il faut ajouter que ses prédécesseurs, Fermat et Pascal, se servaient de même avec avantage (mais comme nous le savons à l'insu de Huygens) de cette analyse pour la résolution de quelques problèmes de jeuGa naar voetnoot2). Pour autant que nous le sachions, Huygens ne s'est occupé qu'une seule fois, en 1668, de cette branche nouvelle des mathématiques, qui se développait pendant sa vie par les travaux de PascalGa naar voetnoot3) et de WallisGa naar voetnoot4). Nous reproduirons en lieu propre ces recherches de Huygens intitulées: ‘De combinationum mirandis’. Une autre particularité de la méthode pratiquée par Huygens, c'est qu'elle amène souvent la solution désirée sous la forme d'une suite infinieGa naar voetnoot5) dans des cas où l'on peut éviter l'usage d'une telle suite en utilisant une voie différenteGa naar voetnoot6). C'est à l'une de ces occasions que Huygens apprit à sommer la suite formée par | |||||||||||||||||||||||||||||||||||||||||
[pagina 21]
| |||||||||||||||||||||||||||||||||||||||||
les fractions qu'on obtient en divisant l'unité par les nombres triangulaires successifsGa naar voetnoot7). Dans tous les autres cas il s'agit de suites de la forme a + 2ar + 3ar2 + + 4ar3 + ... (où a et r sont des fractions données), dont la sommation lui réussit égalementGa naar voetnoot8). | |||||||||||||||||||||||||||||||||||||||||
Le Problème des partis.Le problème des partis remonte jusqu'au quinzième siècleGa naar voetnoot9) et les savants s'en sont encore occupés de notre temps. Laissant de côté les extensions qu'on lui a données plus tard, on peut le formuler comme suit: Les joueurs A, B, C ... jouent à qui aura gagné le premier n parties, leurs chances à chaque partie étant égales. Ils veulent cesser le jeu au moment où il leur manque respectivement a, b, c... parties. Dans quel rapport doivent-ils se partager l'enjeu e? Parlons d'abord du cas de deux joueurs, A et B, et désignons par φ(a, b)e la part de l'enjeu qui revient au joueur A et de même par φ(b, a)e celle qui est due à B. Alors la solution du problème peut être exprimée à volonté par l'une ou l'autre des deux suites:Ga naar voetnoot10)
| |||||||||||||||||||||||||||||||||||||||||
[pagina 22]
| |||||||||||||||||||||||||||||||||||||||||
Après les solutions fausses de Paciuolo (1494), de Cardano (1539) et de Tartaglia (1556)Ga naar voetnoot1), les premières solutions exactes ne furent obtenues qu'après un intervalle de plus d'un siècle par Pascal (1654), Fermat (1654) et Huygens (1656). Parmi ces derniers ce fut Pascal qui, en cette matière, devança de loin ses deux rivaux. Sa solution, telle qu'elle parut dans son ‘Traité du triangle arithmétique’Ga naar voetnoot2), sous l'en-tête ‘Usage du triangle arithmétique pour déterminer les partis qu'on doit faire entre deux joueurs qui jouent en plusieurs parties’, ne diffère pas essentiellement de celle représentée par la formule (1). En effet, les termes qui se trouvent entre crochets dans cette formule, et qui sont des coefficients binomiaux, correspondent un à un aux ‘cellules du triangle’, dont la somme est le dénominateur de la fraction qui détermine chez Pascal la portion revenant au premier joueur. De plus, Pascal a donné des solutions plus simples et très intéressantes pour les cas (n - 1, n) et (n - 2, n). On retrouve facilement la première de ces solutions en remarquant que la suite (1) nous donne:
| |||||||||||||||||||||||||||||||||||||||||
[pagina 23]
| |||||||||||||||||||||||||||||||||||||||||
et qu'on a évidemment:
Ensuite la solution du deuxième cas se déduit immédiatement de celle du premier cas par l'emploi de la relation:
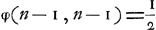 Ga naar voetnoot4). Ga naar voetnoot4).
C'est à l'aide des formules (3)-(5) qu'on arrive aisément aux résultats qui furent communiqués à Huygens par l'intermédiaire de Carcavy dans la lettre du 28 septembre 1656Ga naar voetnoot5); résultats que Pascal avait déjà obtenu en 1654, comme le prouve sa lettre à Fermat du 29 juillet de cette annéeGa naar voetnoot6). D'ailleurs, comme nous l'avons déjà dit dans la note 14 de la p. 7, Pascal savait résoudre de la même façon que Huygens les cas simples du problème des partis, tandis que Fermat y appliquait l'analyse combinatoireGa naar voetnoot7). Huygens, dans son Traité, se contente de son côté de résoudre quelques uns de ces cas simples, où a et b sont des nombres relativement petitsGa naar voetnoot8), et de mon trer comment on peut passer de là à des cas de plus en plus compliquésGa naar voetnoot9).
Parmi les premiers successeurs de Huygens sur le terrain du calcul des probabilités, Struyck ne s'est pas occupé du problème des partis; de Monmort, dans la | |||||||||||||||||||||||||||||||||||||||||
[pagina 24]
| |||||||||||||||||||||||||||||||||||||||||
première édition de 1708 de son ‘Essay’Ga naar voetnoot1) et Jacques Bernoulli dans son ‘Ars conjectandi’Ga naar voetnoot2) ont donné la formule (1); de Moivre a, le premier, étendu la solution au cas où les chances p et q ( 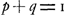 ) des joueurs A et B de gagner une partie sont inégalesGa naar voetnoot3). Dans ce cas les formules (1) et (2) doivent être remplacées par les suivantes: ) des joueurs A et B de gagner une partie sont inégalesGa naar voetnoot3). Dans ce cas les formules (1) et (2) doivent être remplacées par les suivantes:
De ces formules (1a) et (2a) de Moivre a donné la première dans le Mémoire de 1711, cité dans la note 3 de cette page; de Monmort y a ajouté la seconde dans l'édition de 1713 de son ‘Essay’Ga naar voetnoot4). Parmi les mathématiciens plus modernes qui se sont occupés du problème des partis nous citerons Laplace, qui a trouvé la fonction génératriceGa naar voetnoot5) dont le développement suivant les puissances de ses deux variables fait connaître les valeurs de φ(a, b), parce que ces valeurs sont égales aux coefficients des termes du développement, et Meyer qui a réussi à représenter φ(a, b) à l'aide d'une intégrale définie très simpleGa naar voetnoot6).
Dans le cas de n joueurs A1, A2,.... An, auxquels il manque respectivement a1, a2,.. an parties, on a: | |||||||||||||||||||||||||||||||||||||||||
[pagina 25]
| |||||||||||||||||||||||||||||||||||||||||
où p1, p2,..., pn représentent les probabilités que les joueurs ont de gagner une partie et où la sommation doit être étendue à toutes les valeurs entières de u2, u3,..., un pour lesquelles 0 ≦um ≦am - 1Ga naar voetnoot7). Déja Paciuolo (1494) s'était occupé du cas de trois joueursGa naar voetnoot8). Pascal, Fermat et Huygens savaient calculer (en supposant p1 = p2 = p3) pour chaque cas particulier les espérances mathématiques des joueurs; Pascal et Huygens en réduisant la solution du cas donné à celle de cas plus simplesGa naar voetnoot9); Fermat en appliquant l'analyse combinatoireGa naar voetnoot10). C'est en se servant de cette dernière méthode que de Moivre découvrit le premier une règle générale dont l'application ne diffère point de l'emploi de la formule (6)Ga naar voetnoot11). Ajoutons enfin que LaplaceGa naar voetnoot12) et MeyerGa naar voetnoot13) ont su généraliser leurs solutions que nous venons de mentionner, de sorte qu'elles deviennent applicables au cas de n joueurs. | |||||||||||||||||||||||||||||||||||||||||
[pagina 26]
| |||||||||||||||||||||||||||||||||||||||||
Les Problèmes des dés.Le 29 juillet 1654 Pascal écrivit à FermatGa naar voetnoot1): ‘J'admire bien davantage la méthode des parties que celle des dés; j'avois vu plusieurs personnes trouver celle des dés, comme M. le chevalier de Méré, qui est celui qui m'a proposé ces questions, et aussi M. de Roberval; mais M. de Méré n'avoit jamais pu trouver la juste valeur des partiesGa naar voetnoot2) ni de biais pour y arriver, de sorte que je me trouvais seul qui eusse connu cette proportion.’ Pascal avait en vue le problème des dés tel qu'il fut formulé par de Méré. Pour celui-ci il s'agissait de savoir en combien de coups on peut entreprendre avec avantage de jeter deux six avec deux dés, mais l'extension au cas de n dés, et le problème plus général de déterminer en combien de coups on peut gager d'amener un événement quelconque dont la probabilité à chaque coup est égal à p, ne présentent non plus aucune difficulté, pourvu qu'on y emploie le calcul des logarithmes. Huygens l'a montré lui-même dans la Pièce de 1676, destinée à DierkensGa naar voetnoot3), où | |||||||||||||||||||||||||||||||||||||||||
[pagina 27]
| |||||||||||||||||||||||||||||||||||||||||
il obtient par un raisonnement très simple une solution qui, appliquée au probleme général, consiste dans la détermination du plus petit nombre entier excédant le quotient de logs 2 par log (1 - p)Ga naar voetnoot4). Pourquoi donc Huygens s'est-il borné dans son Traité de 1657 aux cas d'un seul et de deux désGa naar voetnoot5) et n'y a-t-il su résoudre le problème dans ce dernier cas que par des calculs qui doivent avoir été assez pénibles? Il est vrai que le calcul des logarithmes ne semble pas avoir fait partie du cours professé par van SchootenGa naar voetnoot6) et qu'on n'en rencontre dans les manusscrits de Huygens aucune trace avant 1661, tandis qu'alors ce calcul est approché par lui du côté géométrique en connection avec la quadrature de l'hyperboleGa naar voetnoot7). Toutefois il semble inadmissible que Huygens n'ait pas pris connaissance avant 1657 d'une branche si importante des mathématiques, sans doute bien connue en Hollande par les travaux de VlackGa naar voetnoot8). En effet, la réponse à la question que nous avons posée est à la fois plus simple et plus curieuse. C'est que Huygens avait attaqué en 1656 le problème du côté le moins accessible. Au lieu de considérer dès l'abord l'espérance mathématique de celui qui donne à jeter, il avait commencé par s'occuper des chances plus compliquées de celui qui jette les dés, de sorte qu'il ne s'était pas aperçu que l'espérance du premier peut être représentée par l'expression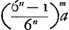 , où a est l'enjeu, n le nombre des dés avec lesquels on doit jeter n six, et m le nombre des coups dont on est convenu. , où a est l'enjeu, n le nombre des dés avec lesquels on doit jeter n six, et m le nombre des coups dont on est convenu.
L'exactitude de cette explication est prouvée indubitablement par l'Appendice VII de 1676, p. 156-163 du présent Tome. On y voit dans quelles circonstances Huygens découvrit enfin la simplification qu'on obtient en s'occupant en premier lieu des chances du ‘contra certans’, comme Huygens l'appelleGa naar voetnoot9). | |||||||||||||||||||||||||||||||||||||||||
[pagina 28]
| |||||||||||||||||||||||||||||||||||||||||
D'ailleurs la Pièce destinée à Dierkens, dont nous avons déjà parléGa naar voetnoot1), nous apprend comment Huygens a profité aussitôt de cette découverte.
Un autre problème des dés, traité par Huygens dans la Prop. XIIGa naar voetnoot2), à savoir ‘Trouver le nombre de dés avec lequel on peut accepter de jeter 2 six du premier coup’, n'admet pas de solution aussi simple que celui que nous venons de considérer. Comme Huygens l'a remarqué il est équivalent ‘à la question de savoir en combien de coups d'un seul dé l'on peut compter jeter deux fois un 6’. Supposons plus généralement qu'il s'agisse d'un événement dont la probabilité à chaque coup est égale à p et qu'on veuille connaître la probabilité qu'il se produise au moins m fois en n coups. Cette probabilité est représentée par la somme des (n - m + 1) premiers termes du développement de (p + q)n, où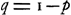 ; la probabilité complémentaire est donnée par les m derniers termes du même développementGa naar voetnoot3). Pour résoudre le problème posé par Huygens il faut donc chercher le plus petit nombre entier pour lequel: ; la probabilité complémentaire est donnée par les m derniers termes du même développementGa naar voetnoot3). Pour résoudre le problème posé par Huygens il faut donc chercher le plus petit nombre entier pour lequel:
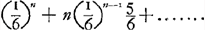
ou bien déduire ce même nombre à l'aide de la relation:
(5/6)n + n (5/6)n - 1 1/6 < ½.
Il est évident que c'est la seconde formule qui mène le plus facilement au but désiré. Or, le calcul effectué par Huygens correspond à l'emploi de la première. | |||||||||||||||||||||||||||||||||||||||||
[pagina 29]
| |||||||||||||||||||||||||||||||||||||||||
Les Exercices proposés aux lecteurs du Traité de 1657.Les Exercices qu'on trouve vers la fin du Traité de 1657Ga naar voetnoot4) n'ont pas manqué le but ‘de laisser quelque chose à chercher’ aux ‘lecteurs, afin que cela leur servît d'exercice et de passe-temps’Ga naar voetnoot5). En effet, parmi les savants qui se sont occupés à les résoudre: HuddeGa naar voetnoot6), SpinozaGa naar voetnoot7), de Mon- | |||||||||||||||||||||||||||||||||||||||||
[pagina 30]
| |||||||||||||||||||||||||||||||||||||||||
mortGa naar voetnoot1), de MoivreGa naar voetnoot2), Jacques BernoulliGa naar voetnoot3) et StruyckGa naar voetnoot4), on rencontre quelques noms des plus illustres. Si donc ces problèmes, avec les généralisations auxquelles ils conduisent naturellement, ont exercé une influence incontestable sur le développement du calcul des probabilités, Huygens en doit partager l'honneur avec Fermat et Pascal qui lui avaient proposé respectivement, Fermat le premier et le troisième, Pascal le dernier des cinq ExercicesGa naar voetnoot5). Pour des informations plus détaillées sur chaque Exercice en particulier nous préférons renvoyer le lecteur aux notes des p. 88-91. | |||||||||||||||||||||||||||||||||||||||||
[pagina 31]
| |||||||||||||||||||||||||||||||||||||||||
Problèmes échangés entre Huygens et Hudde sur l'avantage ou le désavantage de la primauté.Cas où l'enjeu, quelle qu'en soit la grandeur, peut être gagné d'un seul coup.Afin de découvrir le fil qui nous conduira à travers le dédale des problèmes que Huygens et Hudde se sont proposés en 1665, et des malentendus qui en sont résultés, nous commencerons par résoudre le problème qui suit:
A et B jettent à tour de rôle. Lorsque le coup leur est favorable ils prennent tout ce qui se trouve à l'enjeu et la partie est finie; s'il leur est défavorable ils ajoutent | |||||||||||||||||||||||||||||||||||||||||
[pagina 32]
| |||||||||||||||||||||||||||||||||||||||||
un ducat à l'enjeu. Soit α la probabilité, quand c'est le tour de A de jeter, que le coup lui soit favorable et α′ la probabilité complémentaire ( 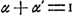 ); soient β et β′ les probabilités correspondantes dans le cas de B. Supposons que les joueurs se séparent à un instant où l'enjeu est monté à n ducats, comment doivent-ils se partager cet enjeu, 1o. dans le cas où c'est le tour de A de jeter 2o. dans le cas où c'est le tour de B? ); soient β et β′ les probabilités correspondantes dans le cas de B. Supposons que les joueurs se séparent à un instant où l'enjeu est monté à n ducats, comment doivent-ils se partager cet enjeu, 1o. dans le cas où c'est le tour de A de jeter 2o. dans le cas où c'est le tour de B?
Représentons par φ(n) la part qui revient à A dans le premier cas, par ψ(n) celle qui est due à B dans le second cas. On a alors suivant les règles du jeu:
Or, on peut considérer la part de A comme la somme de deux parties dont l'une se rapporte à sa chance, au cas où le jeu eût été continué, d'obtenir l'enjeu actuel, et l'autre à ses chances de gagner dans ce cas, outre l'enjeu actuel, les ducats ajoutés par son adversaire pendant la continuation du jeu ou bien de perdre ceux qu'il y aurait dû ajouter lui-même. Évidemment la première de ces parties est proportionnelle à l'enjeu n, tandis que l'autre est une quantité constante puisque la chance que le jeu finira ou ne finira pas par un coup donné est indépendante de la grandeur de l'enjeu. On peut donc poser:
et de même:
Or, la substitution de ses expressions dans les équations (3) et (4) nous fournit, puisque a1, a2, b1 et b2 sont indépendants de n: 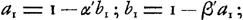
d'où il s'ensuit: 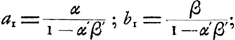
| |||||||||||||||||||||||||||||||||||||||||
[pagina 33]
| |||||||||||||||||||||||||||||||||||||||||
et par conséquent:
On trouve donc p.e.:
et l'on a dans le cas α = α′ = β = β′ = 1/2:
Prenons maintenant le premier problème sur le désavantage de la primauté, tel qu'il fut proposé par Huygens à Hudde dans sa lettre du 4 avril 1665Ga naar voetnoot3). Ce problème avait été formulé par Huygens comme suit:Ga naar voetnoot4)
‘A et B jettent à tour de rôle croix ou pile, sous condition que celui qui jette pile mettra chaque fois un ducat, mais que celui qui jette croix prendra tout ce qui | |||||||||||||||||||||||||||||||||||||||||
[pagina 34]
| |||||||||||||||||||||||||||||||||||||||||
est mis, et A jette le premier, pendant que rien n'a été mis encore. La question est, combien A perd, quand il entre dans ce jeu, on combien il pourrait donner à B pour pouvoir en finir?’
Or, Huygens en posant cette question avait sous-entendu que ‘le jeu ne devait pas finir avant que quelque chose n'eût été mis de part ou d'autre’Ga naar voetnoot1). Dans ce cas on a pour calculer la perte p de A: 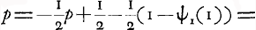
c'est-à-dire, en appliquant la formule (11): 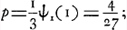
résultat qui fut, en effet, obtenu par HuygensGa naar voetnoot2). Hudde, au contraire, avait compris, que si A jetait croix du premier coup le jeu serait fini. Dans cette hypothèse on a: 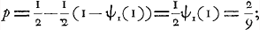
résultat que Hudde communiqua à Huygens dans sa lettre du 5 maiGa naar voetnoot3) (p. 350 du T. V).
Dans cette dernière lettre Hudde ne se borna pas à indiquer sa solution du problème que nous venons de considérer, mais il posa de son côté la question suivanteGa naar voetnoot4): | |||||||||||||||||||||||||||||||||||||||||
[pagina 35]
| |||||||||||||||||||||||||||||||||||||||||
‘A et B tirent à l'aveuglette à tour de rôle. A toujours 1 de 3 jetons, desquels trois il y en a deux blancs et un noir, B de même toujours d'un certain nombre de jetons blancs et noirs dont la proportion reste invariable; sous condition que celui qui tire un jeton blanc jouira de tout ce qui est mis, mais qu'au contraire celui qui tire un noir ajoutera toujours un ducat: et A tirera le premier avant que rien n'ait été mis. On demande, lorsqu'on veut avoir des conditions équivalentes de part et d'autre, de sorte que, A commençant à tirer, il n'y ait d'avantage pour aucun des deux, quelle proportion devra se trouver entre les dits jetons blancs et noirs?’
Pour résoudre ce problème suivant l'interprétation de Huygens nous représenterons par εA l'espérance mathématique de A et par εB celle de B, lorsque c'est le tour de A de tirer et que rien n'a encore été mis. On a donc, en employant les notations de la p. 32: 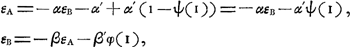 | |||||||||||||||||||||||||||||||||||||||||
[pagina 36]
| |||||||||||||||||||||||||||||||||||||||||
et par conséquent: 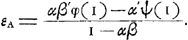 En substituant dans cette dernière formule les expressions que nous avons déduites pour φ(1) et ψ(1)Ga naar voetnoot1), on trouve facilement (en utilisant les relations
En substituant dans cette dernière formule les expressions que nous avons déduites pour φ(1) et ψ(1)Ga naar voetnoot1), on trouve facilement (en utilisant les relations 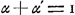 et et 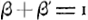 ): ):
La condition de l'égalité des chances de A et de B au commencement du jeu exige donc que le rapport β: β′ entre les jetons blancs et noirs de B soit égal à la racine positive de l'équation: 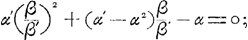
équation qui dans le cas du problème (où α = 2/3, α′ = 1/3) nous donne: 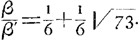
Ce sont là, en effet, les résultats obtenus par Huygens, qu'il communiqua à Hudde dans ses lettres du 7 juillet et du 28 juilletGa naar voetnoot2). Passons maintenant à l'interprétation de Hudde. D'après elle on a:
L'égalité des chances exige donc en général:
β/β′ = α | |||||||||||||||||||||||||||||||||||||||||
[pagina 37]
| |||||||||||||||||||||||||||||||||||||||||
et dans le problème spécial proposé par Hudde:
β/β′ = 2/3;
résultats qu'il annonça à Huygens dans sa lettre du 29 juinGa naar voetnoot3).
Voulant examiner encore d'une autre manière si, en effet, ses ‘calculs’ à lui et ceux de Hudde ‘suivaient des voies différentes’, Huygens demanda à HuddeGa naar voetnoot4) s'il trouvait, comme lui, 207/343 d'un ducat pour l'avantage de A, qui fait le premier coup, dans le cas où A dispose de deux jetons blancs et d'un noir et B d'un blanc et de deux noirs. On retrouve facilement le résultat mentionné en substituant dans la formule (12) de la p. 36 pour α, α′, β et β′ les valeurs 2/3, 1/3, 1/3 et 2/3. La même substitution appliquée à la formule (13) fournit, au contraire, 3/49 d'un ducat. Sans doute ce dernier résultat eût été indiqué par Hudde dans sa réponse si le nouveau malentendu dont nous avons parlé dans le deuxième alinéa de la note 3 de la p. 34 n'était intervenu. On peut s'en convaincre en consultant les pp. 415-416 et 446 du T. V, où l'on voit de quelle manière Hudde avait obtenu la solution 9/245 qu'il communiqua à Huygens dans sa lettre du 29 juinGa naar voetnoot5). Ici, comme partout, les calculs et les raisonnements de Hudde sur les questions dont nous traitons étaient parfaitement exacts, les divergences entre ses résultats et ceux de Huygens ne provenant que des interprétations différentes qu'ils donnèrent à ces questions. | |||||||||||||||||||||||||||||||||||||||||
[pagina 38]
| |||||||||||||||||||||||||||||||||||||||||
Voici un autre problème proposé par Huygens dans sa lettre du 10 maiGa naar voetnoot1):
‘A et B jettent à tour de rôle à croix ou pile, à condition que celui qui jette pile mettra un ducat, mais que celui qui jette croix prendra tout ce qui est mis; et A jettera le premier. On demande combien A et B devraient mettre dès le commencement, c'est-à-dire, chacun une somme égale, pour faire que la condition de A et de B devienne la même?’
Sur ce problème la différence d'interprétation concernant l'effet du premier coup s'il était croix et que rien ne fût encore mis, ne trouvait pas de prise; par suite, les résultats obtenus par Huygens et Hudde étaient identiques. Évidemment l'égalité des conditions des deux joueurs exige ici: 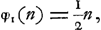
c'est à direGa naar voetnoot2): 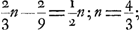
il faut donc que chaque joueur commence par mettre 2/3 d'un ducat. Ce résultat fut indiqué par Hudde dans sa lettre du 29 juinGa naar voetnoot3) et par Huygens dans la sienne du 7 juillet 1665Ga naar voetnoot4). | |||||||||||||||||||||||||||||||||||||||||
Un dernier problème proposé par Huygens à Hudde en 1665. La ‘part du diable’.Nous avons réservé une place à part au problème suivantGa naar voetnoot5):
‘A et B jettent à tour de rôle croix ou pile, à condition que celui qui jette pile mettra chaque fois un ducat à l'enjeu, mais celui qui jette croix recevra chaque | |||||||||||||||||||||||||||||||||||||||||
[pagina 39]
| |||||||||||||||||||||||||||||||||||||||||
fois un ducat si quelque chose a été mis. Et A jettera le premier quand il n'y a encore rien à l'enjeu, et le jeu ne finira pas avant que quelque chose ait été mis, et l'on jouera jusqu'à ce que tout ait été enlevé. On demande quel est le désavantage de A?’
De ce problème Huygens a élaboré une solution sous la date du 15 juillet 1665Ga naar voetnoot6). Il l'a aussi proposé à Hudde puisque celui-ci en a traité dans une pièce que nous avons reproduite aux p. 463-469 du T. V. Au premier abord le problème n'a rien de bien particulier. Il semble même que sa solution puisse être obtenue par un raisonnement très simpleGa naar voetnoot7) que nous exposons dans la note 2 de la p. 142 et qui évidemment a échappé à l'attention de HuygensGa naar voetnoot8). Il y a cependant une réserve importante à faire dont nous parlerons plus loinGa naar voetnoot9). Nous commençons par développer ici ce raisonnement d'une manière un peu plus générale que nous ne le faisons à la place précitée. Supposons, à cet effet, que les joueurs A et B conviennent de se séparer à un instant où il y n ducats à l'enjeu, et soit xn la part qui revient au joueur dont c'est le tour de jeter. Nous divisons en deux périodes le jeu qui aurait eu lieu si les joueurs avaient continué. Nous étendons la première période jusqu'à l'instant où pour la première fois l'enjeu est réduit à un seul ducat et la séconde depuis cet instant jusqu'à la fin du jeu. Évidemment l'espérance mathématique correspondant aux ducats que le joueur peut gagner ou perdre pendant la première période est égale à son espérance totale dans le cas où il y a n-1 ducats à l'enjeu, c'est-à-dire elle est égale à xn-1. Quant à son espérance correspondant à la seconde période, elle est égale à x1 dans le cas où n est impair, parce que dans ce cas le tour de jeter sera au commencement de cette période au même joueur qui a jeté lors- | |||||||||||||||||||||||||||||||||||||||||
[pagina 40]
| |||||||||||||||||||||||||||||||||||||||||
qu'il y avait n ducats à l'enjeu; dans le cas où n est pair son espérance sera, au contraire, représentée par 1 - x1Ga naar voetnoot1), l'unité étant égale à un ducat. On a donc: 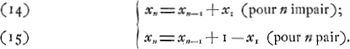 Dans le cas spécial n = 2, on trouve:
Soient maintenant, au début du jeu, εA l'espérance du joueur qui jette le premier, εB celle de l'autre joueur. D'après les règles du jeu, on a: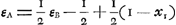 , puisque A s'il jette croix se trouvera après ce coup dans la même situation que celle où B se trouvait au commencement du jeu. Mais, parce qu'on a , puisque A s'il jette croix se trouvera après ce coup dans la même situation que celle où B se trouvait au commencement du jeu. Mais, parce qu'on a 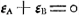 Ga naar voetnoot1), cette équation se réduit à: Ga naar voetnoot1), cette équation se réduit à:
On a de plus:
et, par conséquent, à cause de la relation (16):
donc enfin:
résultat obtenu par HuygensGa naar voetnoot2) et aussi par HuddeGa naar voetnoot3). | |||||||||||||||||||||||||||||||||||||||||
[pagina 41]
| |||||||||||||||||||||||||||||||||||||||||
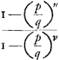
Quant aux équations (14) et (15), elles se réduisent à la seule équation: 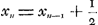 , applicable lorsque n est pair ou impair. Et l'on trouve facilement à l'aide de cette équation: , applicable lorsque n est pair ou impair. Et l'on trouve facilement à l'aide de cette équation:
Nous indiquons ci-après une autre solution ne reposant pas sur le raisonnement qui nous a fourni la valeur de x2. Elle nous fera connaître l'artifice sur lequel la solution de Huygens est fondée. On a d'abord comme conséquence immédiate des règles du jeuGa naar voetnoot5);
ou bien:
À l'aide d'une application répétée de cette dernière relation on exprime facilement x3, x4, x5, etc. en fonction de x2 et de x1. On trouve: 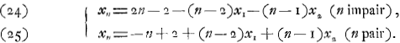 | |||||||||||||||||||||||||||||||||||||||||
[pagina 42]
| |||||||||||||||||||||||||||||||||||||||||
Or, il résulte des équations (17) et (18):
Les équations (23) et (24) se réduisent donc aux suivantes:
que nous écrivons:  À l'exemple de HuygensGa naar voetnoot1) nous raisonnons maintenant de la manière suivante: Même si n est un grand nombre, les espérances des deux joueurs ne peuvent différer que de 1 ou de 2 ducats, puisque la différence entre les chances du joueur qui jette le premier et de l'autre joueur ne peut se faire sentir que vers la fin de la partie quand il n'y a plus qu'un petit nombre de ducats à l'enjeu. Soit donc p cette différence. On a alors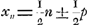 . Substituons cette valeur de xn dans les équations (28) et (29) et faisons croître indéfiniment le nombre n. Ces équations amènent alors l'une et l'autre le même résultat, savoir εA = - 1/6. . Substituons cette valeur de xn dans les équations (28) et (29) et faisons croître indéfiniment le nombre n. Ces équations amènent alors l'une et l'autre le même résultat, savoir εA = - 1/6.
Disons enfin quelques mots à propos de la solution de Huygens. Huygens commence par déduire deux équations qui sont équivalentes à nos équations (17) et (18)Ga naar voetnoot2). Ensuite il se sert d'une série d'équationsGa naar voetnoot3) qui ne diffèrent pas essentiellement de celles qu'on obtient en prenant successivement n = 2, n = 3, etc. | |||||||||||||||||||||||||||||||||||||||||
[pagina 43]
| |||||||||||||||||||||||||||||||||||||||||
dans l'équation (22)Ga naar voetnoot4). De cette manière Huygens réussit à exprimer la quantité -a= εA à l'aide d'une suite qu'on peut prolonger indéfinimentGa naar voetnoot5). Il lui faut donc prouver qu'on peut négliger le dernier terme de cette suite quand on la prolonge sussisammentGa naar voetnoot6). C'est à quoi il emploie le raisonnement que nous venons de reproduire. Après cela il ne s'agit plus que de sommer la suite en question; ce qui lui réussit égalementGa naar voetnoot7). Remarquons que cette solution de Huygens contraste favorablement avec celle de Hudde. Dans la première Pièce qui se rapporte à cette dernière solutionGa naar voetnoot8), Hudde n'a trouvé d'autre issue que d'ériger en ‘Corollaire’ une relation qui dans nos notations s'exprime par: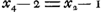 . Dans une autre PièceGa naar voetnoot9) il tâche de prouver la relation . Dans une autre PièceGa naar voetnoot9) il tâche de prouver la relation 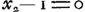 par un développement en série dans lequel il néglige en dernière instance un grand nombre de termes dont les valeurs lui sont inconnues. par un développement en série dans lequel il néglige en dernière instance un grand nombre de termes dont les valeurs lui sont inconnues.
Nous avons maintenant à nous occuper de la réserve qui nous empêche d'accepter sans discussion les solutions dont nous venons de traiter. Ces solutions supposent que la somme des espérances des deux joueurs est égale à l'enjeu. Or, cette hypothèse devient ici sujette à caution parce que le jeu peut se prolonger indéfiniment sans que l'enjeu soit jamais épuisé. Afin de montrer la portée de cette remarque, supposons que les joueurs conviennent de donner l'enjeu à une troisième personne dans le cas où cet enjeu monterait à v ducats. Quelle est l'espérance mathématique φc(n, v) de cette personne à l'instant où l'enjeu contient n ducats (n < v)?.
On a évidemment: φc(1, v) = 1/2 φc(2, v), et de même: | |||||||||||||||||||||||||||||||||||||||||
[pagina 44]
| |||||||||||||||||||||||||||||||||||||||||
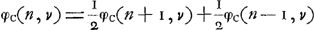 (pour 1 <n <v). (pour 1 <n <v).
De ces relations on déduit facilement: φc(n, v) = nφc(1, v) (pour 1 ≦ n ≦ v). Or, φc(v, v) = v, donc φc(1, v) = 1, et par suite:
Soit maintenant εc l'espérance de la troisième personne au début du jeu, rien n'étant encore mis. On a: 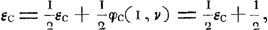
et, par conséquent:
L'espérance de la troisième personne est donc indépendante du nombre v. Elle est égale à un ducat au commencement du jeu et elle augmente ou diminue ensuite régulièrement avec l'enjeu auquel elle reste toujours égale.
Quelle est la probabilité que l'enjeu après être monté à n ducats atteigne la somme de v ducats?
On obtient cette probabilité en divisant l'espérance de la troisième personne par la somme qu'il peut obtenir. Elle est donc égale à n/v quand 1 ≦ n ≦ v, et à 1/v quand rien n'a encore été mis. La probabilité que la troisième personne gagne l'enjeu s'approche donc indéfiniment de zéro à mesure que v augmente. Pour v = 2n elle est égale à 1/2. Or, puisque la probabilité que l'enjeu diminue de n à 0, sans passer par v = 2n, est évidemment égale à celle qu'il monte de n à v = 2n (sans passer par zéro), il ne reste rien pour la probabilité que l'enjeu oscille indéfiniment entre les limites 0 et 2n sans jamais atteindre ni l'une ni l'autre. Quoique cet événement ne soit pas impossible, sa probabilité est donc infiniment petite. Et si cela est vrai pour v = 2n, il en est de même a fortiori pour v = 2n - 1, | |||||||||||||||||||||||||||||||||||||||||
[pagina 45]
| |||||||||||||||||||||||||||||||||||||||||
c'est-à-dire la conclusion reste applicable dans le cas où la limite supérieure est désignée par un nombre impair.
Quelles sont l'espérance φA(n, v) du joueur qui doit jeter, et celle φB(n, v) de l'autre joueur?
Il faut dans le développement postérieur du jeu distinguer trois possibilités: 1e l'enjeu est épuisé par les joueurs, 2e il est gagné par la troisième personne, 3e il oscille indéfiniment entre 0 et v ducats sans jamais atteindre une de ces deux limites. Ce dernier événement entraînerait pour les joueurs une perte n'excédant jamais v ducats; perte qu'on peut négliger puisque sa probabilité est infiniment petite comme nous venons de le voir. On a donc: 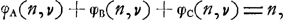
c'est-à-dire, à cause de l'équation (30):
En appliquant les règles du jeu, on trouve: 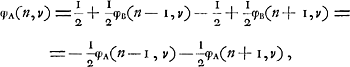 ou bien: 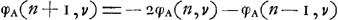 (pour 1 <n < v). (pour 1 <n < v).
On a de plus: 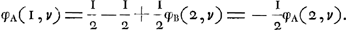
À l'aide de ces deux dernières relations on trouve sans peine: 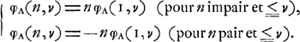 Or, évidemment φA(v, v) = 0, donc: | |||||||||||||||||||||||||||||||||||||||||
[pagina 46]
| |||||||||||||||||||||||||||||||||||||||||
Calculons maintenant les espérances ε′A et ε′B des joueurs A et B au début du jeu. On a: 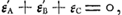
c'est-à-dire, puisque εc = 1: 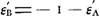
Or, d'après les règles du jeu: 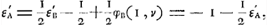
et par suite:
En comparant ce résultat à celui de la p. 40 on voit que la perte causée aux joueurs par la participation supposée de la troisième personne se répartit également sur les deux joueurs.
Revenons maintenant au problème tel qu'il fut posé par Huygens. Il n'y est question que des deux joueurs A et B. Cependant il n'y a pas lieu, nous semble-t-il, de leur assigner l'espérance mathématique qui, d'après nos calculs, revient à la troisième personne que nous avons introduite. Dès que la formation de l'enjeu a commencé ces joueurs se trouvent dans la situation que nous avons indiquée dans la note 1 de cette page, pourvu qu'on y suppose v = ∞; c'est-à-dire l'enjeu doit être considéré comme perdu pour eux, puisque leurs espérances mathématiques sont devenues égales à zéro. On arrive à cette conclusion si l'on fait croître indé- | |||||||||||||||||||||||||||||||||||||||||
[pagina 47]
| |||||||||||||||||||||||||||||||||||||||||
finiment le nombre v. Il est vrai que la probabilité que le jeu continue jusqu'à l'infini est infiniment petite, mais l'espérance mathématique qui correspond à cette éventualité n'en reste pas moins une quantité finie. Elle est égale à chaque instant à l'enjeu actuel. Remarquons que des considérations analogues se présentent dans tous les jeux où les coups peuvent se répéter indéfiniment sans épuiser l'enjeu, de sorte qu'il nous semble utile d'introduire un terme pour désigner la somme qui dans un tel jeu est perdue pour les joueurs à l'instant même où ils conviennent de jouer. Nous proposons de la nommer: la part du diable. N'oublions pas cependant que parfois dans les jeux de ce genre il est facile de montrer dès l'abord que cette part est infiniment petite, et par suite négligeable. Prenons par exemple le problème de la p. 31. La probabilité qu'un enjeu de n ducats monte sous les conditions de ce problème jusqu'a n + v ducats s'exprime pour v pair par α′½vβ′½v, et pour v impair par α′½(v + 1) β′½(v - 1). La ‘part du diable’ est donc dans ce cas égale à la limite, pour v = ∞, du produit de ces expressions par n + v, c'est-à-dire qu'elle est nulle. Afin de résoudre ce problème, il est donc permis, comme nous l'avons faitGa naar voetnoot2), d'appliquer l'hypothèse que la somme des espérances des joueurs est à chaque instant égale à l'enjeuGa naar voetnoot3). | |||||||||||||||||||||||||||||||||||||||||
[pagina 48]
| |||||||||||||||||||||||||||||||||||||||||
Nous finissons par indiquer de quelle manière la part du diable peut être éliminée par un changement dans l'énoncé du problème qui nous occupe. Il suffit pour cela d'ajouter à cet énoncé la clause suivante: Lorsque l'enjeu monte à une certaine somme les joueurs se le partageront en parties égales sans continuer le jeu. Évidemment il faut alors ajouter à l'espérance de chaque joueur la moitié de ce que nous avons trouvé pour l'espérance de la troisième personneGa naar voetnoot1). On a donc dans ce cas: 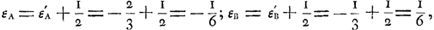
et de même: 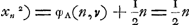 Ga naar voetnoot2) Ga naar voetnoot2)
résultats conformes à ceux de HuygensGa naar voetnoot3). |
| ||||||||||||||||||||||||||||||||||||||||


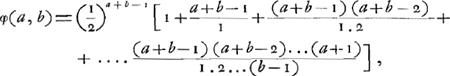
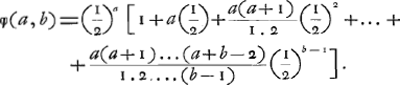
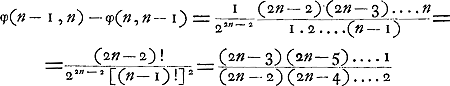
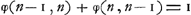
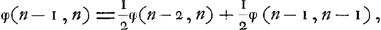
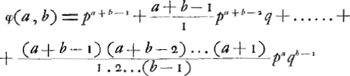
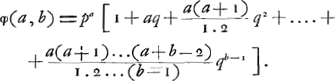
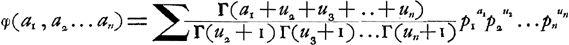
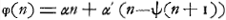
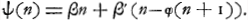
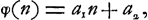
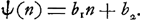
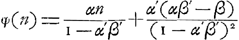
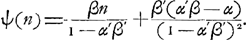
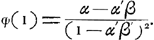
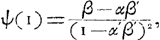
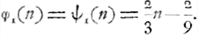
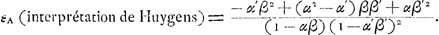
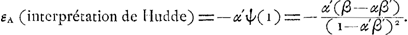
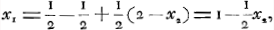
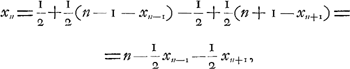
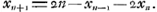 .
.