Oeuvres complètes. Tome XIV. Probabilités. Travaux de mathématiques pures 1655-1666

(1920)–Christiaan Huygens– rechtenstatus

Tables.

I. Pièces et mémoires.

	Page.
VAN REKENINGH IN SPELEN VAN GELUCK. 1656-1657. [DU CALCUL DANS LES JEUX DE HASARD]	1-91
Avertissement	3-48
Titres en fac-similé	50-53
Au lecteur	54-55
À Monsieur Franciscus van Schooten	56-59
Hypothèse fondamentale	61
Propos. I. Avoir des chances égales d'obtenir a ou b me vaut	63
Propos. II. Avoir des chances égales d'obtenir a, b ou c me vaut	65
Propos. III. Avoir p chances d'obtenir a et q d'obtenir b, les chances étant équivalentes, me vaut	65
Propos. IV. Supposons que je joue contre une autre personne à qui aura gagné le premier trois parties, et que j'aie déjà gagné deux parties et lui une. Je veux savoir quelle partie de l'enjeu m'est due au cas où nous voulons interrompre le jeu et partager équitablement les mises	67
Propos. V. Supposons qu'il me manque une partie à moi et trois à mon adversaire. Il s'agit de partager l'enjeu dans cette hypothèse	69
Propos. VI. Supposons qu'il me manque deux parties et qu'il en manque trois à mon adversaire	71
Propos. VII. Supposons qu'il me manque encore deux parties et lui quatre	71
Propos. VIII. Supposons maintenant que trois personnes jouent ensemble et qu'il manque une partie à la première ainsi qu'à la deuxième, mais qu'il en manque deux à la troisième	73
Propos. IX. Pour calculer la part de chacun d'un nombre donné de joueurs, auxquels

		Page.
	manquent des parties en nombres donnés pour chacun d'eux séparément, il faut d'abord se rendre compte de ce qui reviendrait à celui dont on veut savoir la part dans le cas où lui et dans ceux où chacun des autres à son tour aurait gagné la première partie suivante. En ajoutant toutes ces parts et en divisant la somme par le nombre des joueurs on trouve la part cherchée du joueur considéré	73
Propos. X. Trouver en combien de fois l'on peut accepter de jeter un six avec un dé		79
Propos. XI. Trouver en combien de fois l'on peut accepter de jeter 2 six avec 2 dés		81
Propos. XII. Trouver le nombre de dés avec lequel on peut accepter de jeter 2 six du premier coup		83
Propos. XIII. Dans l'hypothèse que je joue un coup de deux dés contre une autre personne à condition que s'il vient 7 points, j'aurai gagné, mais qu'elle aura gagné s'il en vient 10, et que nous partagerons l'enjeu en parties égales s'il vient autre chose, trouver la part qui revient à chacun de nous		85
Propos. XIV. Si un autre joueur et moi jettent tour à tour 2 dés à condition que j'aurai gagné dès que j'aurai jeté 7 points et lui dès qu'il en aura jeté 6, tandis que je lui laisse le premier coup, trouver le rapport de ma chance à la sienne		87
Exercices		89
Appendice I. [1656]
	S'il reste 1 jeu à gagner à A et 1 à B, et 2 jeux à C, combien vaudra la place de chacun supposé qu'ils aient mis chacun 2 écus au jeu? Et s'il reste 1 jeu à gagner à A, 2 à B et 2 à C, 6 écus au jeu? Et encore s'il reste 1 à A, 2 à B, 3 à C, 6 écus au jeu?	92
Appendice II. [1665]
	Solutions du deuxième et du quatrième des Exercices	96
Appendice III. [1665]
	Jean a 2 jetons blancs et 1 noir, mais Pierre 1 blanc et 2 noirs. Et chacun à son tour choisit à l'aveuglette un de ses jetons. Celui qui obtient un jeton noir doit ajouter un ducat à l'enjeu, mais celui qui obtient un jeton blanc reçoit tout ce qui a été mis. Et Jean choisit la première fois, quand il n'y a encore rien à l'enjeu. On demande combien est l'avantage ou le désavantage de Jean au commencement du jeu	102
Appendice IV. [1665]
	A et B choisissent à l'aveuglette à tour de rôle, A toujours un de θ + λ jetons dont θ blancs et λ noirs, mais B un d'un nombre inconnu de jetons blancs et noirs, à condition que celui qui tirera un jeton blanc aura tout ce qui est mis; mais celui qui tire un jeton noir ajoutera chaque fois un ducat à l'enjeu, et A tirera le premier. On demande lorsqu'on veut que les chances de A et de B soient équivalentes, quelle proportion devra exister entre les nombres des jetons blancs et noirs de B	108
	Quel est l'avantage de A qui tire le premier lorsqu'il a θ jetons blancs et λ noirs, et B φ blancs et ψ noirs?	113

		Page.
Appendice V. 1665
	A joue croix ou pile contre B; les deux joueurs jettent tour à tour à condition que celui qui amène pile mettra chaque fois un ducat, mais qui jette croix prendra tout ce qui est mis; et A jettera le premier, alors qu'on n'a encore rien mis. Et il est entendu que le jeu ne finira pas avant que quelque chose ait été mis et enlevé; quel est l'avantage de A?	116
	Explication des calculs de l'Appendice III	124
	Explication des calculs de l'Appendice IV	126
	Quelle doit être dans le jeu de croix ou pile la somme que chaque joueur doit mettre au début (chacun la même somme) afin que A qui jette le premier ait une chance aussi bonne que B?	130
	A et B jettent à tour de rôle croix ou pile, à condition que celui qui jette pile mettra chaque fois un ducat à l'enjeu, mais celui qui jette croix recevra chaque fois un ducat si quelque chose a été mls. Et A jettera le premier quand il n'y a encore rien à l'enjeu et le jeu ne finira pas avant que quelque chose ait été mis, et l'on jouera jusqu'à ce que tout a été enlevé. On demande quel est le désavantage de A	132
	Déterminer la somme de la suite des valeurs réciproques des nombres triangulaires	144
Appendice VI. 1676
	Solution et généralisation du dernier des Exercices	151
Appendice VII. [1676]
	Solution par les logarithmes de ‘problèmes des dés’ identiques ou analogues à ceux des Prop. X et XI	156
Appendice. VIII [1679]
	Avantages du banquier au jeu de la bassette	164
Appendice IX. [1688]
	A, B, C jouent au piquet mettant chacun un ducat. Ce sont toujours deux des trois qui jouent. Celui qui perd met de nouveau un ducat. Et celui qui fait perdre ses deux adversaires consécutivement prend tout. On demande combien est l'avantage de A, s'il a jeté de manière à rester libre pendant la première partie	169
	A, B, C qui jouent mettent chacun un ducat. A joue d'abord contre B et celui des deux qui gagne joue contre C. Et si C gagne il joue de nouveau contre le troisième, jusqu'à ce que quelqu'un gagne 2 fois consécutivement, lequel prend alors l'enjeu et en outre le ducat que chacun qui perd une partie doit ajouter à l'enjeu. On demande la valeur de leurs chances	172
	Solution du problème simplifié où l'on ne met rien que les 3 premiers ducats	173
	Reprise du problème plus compliqué	176
	Solution du problème lorsque le jeu commence sans qu'il y ait une mise	178
TRAVAUX MATHÉMATIQUES DIVERS DE 1655 à 1659		181-407
Avertissement		183-207
	I. 1655. Construire un triangle rectangle, lorsqu'on donne la somme des côtés

		Page.
	droits et la différence des segments dans lesquels l'hypoténuse est divisée par la perpendiculaire abaissée du sommet de l'angle droit	208
II.	1656. Construire les asymptotes d'une hyperbole qui constitue la solution du problème de Pappus ‘proposé en quatre lignes’	210
III.	1657. Trouver un nombre qui ajouté à son carré fait un carré	212
	Pourquoi chaque nombre premier augmenté ou bien diminué de l'unité devient divisible par 6, de même par 4? excepté 2 et 3	213
	Discussion de l'équation diophantine, dite de Pell,	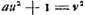213
	Reconnaître si un nombre donné est un non-carré	217
	Lorsqu'un nombre divisé par 9 n'a pour résidu ni 1, ni 8, ni 0, ce ne sera pas un cube	218
	Déterminer le résidu de la division d'un nombre par 7 ou par 11	218
	Reconnaître si un nombre donné est un non-carré. Suite	222
	Appendice I. [1658]. Discussion de l'équation diophantine	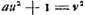225
	Appendice II. [1657] Reconnaître si un nombre donné est un non-carré ou un non-cube	229
IV.	[1657]. Discussion de l'équation de la droite et du cercle	230
V.	1657. Démonstration de Huygens du théorème de Pythagore	232
VI.	1657. Réduction de la rectification de la parabole à la quadrature de l'hyperbole et de la quadrature de la surface du conoïde parabolique à celle du cercle.	234-270
	Première Partie. Découvertes faites le 27 octobre 1657	234
	Deuxième Partie. Réduction, suivant la méthode des anciens, de la rectification de la parabole à la quadrature de l'hyperbole	237
	Troisième Partie. Réduction, suivant la méthode des anciens, de la quadrature de la surface courbe du conoïde parabolique à la quadrature du cercle.	254
VII.	1657. Trouver un cercle qui touche à deux cercles donnés et duquel une droite donnée découpe un arc capable d'un angle donné	271
VIII.	1657. Quadrature des paraboles de divers degrés. Cubature de leurs solides de révolution. Détermination des centres de gravité des segments plans et solides.	273
	Appendice I. [1657], Rédaction à la mode des anciens d'une partie du texte précédent	283
	Appendice II. [1657]. Quadrature des hyperboles de divers degrés	288
IX.	[1657-1658]. Recherches de 1657 et 1658 sur quelques lignes courbes. Perles de de Sluse. Courbe que de Sluse avait rencontrée chez les anciens. Folium de Descartes. Conchoïde. Cissoïde. Parabole. Quadratures. Cubatures de solides de révolution. Tangentes. Points d'inflexion. Centres de gravité. Plus grande largeur de la boucle du folium. Propriétés des diamètres d'une parabole.	294
X.	1658. Réduction de la quadrature de la surface du conoïde elliptique allongé à la quadrature du cercle, et réduction de celle des surfaces du conoïde elliptique aplati et du conoïde hyperbolique à la quadrature de l'hyperbole	314-346

		Page.
	Première Partie. Découvertes faites le 3 février 1658	314
	Deuxième Partie. Relation entre les quadratures des surfaces du sphéroïde aplati et du conoïde hyperbolique	324
	Troisième Partie. Résumé des résultats obtenus dans les Parties qui précèdent	334
	Quatrième Partie. Avantages et désavantages de la méthode des indivisibles comparée à celle des anciens. Description schématique de la méthode de démonstration archimédienne. Rédaction plus soignée des résultats obtenus dans la deuxième Partie, qui concernent les courbes adjointes de la parabole, de l'ellipse et de l'hyperbole	337
XI.	1658-1659. Recherches sur les propriétés géométriques de la cycloïde	347-376
	Première Partie. Quadrature de la cycloïde. Cubature de ses solides de révolution. Centre de gravité de segments cycloïdaux	347
	Deuxième Partie. Centre de gravité du solide engendré par une demi-révolution d'un segment cycloïdal autour de sa corde	358
	Troisième Partie. Rectification, et détermination du centre de gravité, d'un arc cycloïdal. Quadrature de la surface engendrée par la révolution autour de la corde	363
	Quatrième Partie. Démonstration géométrique de la construction de la tangente à la cycloïde	374
	Cinquième Partie. Centre de gravité d'une demi-cycloïde	376
	Appendice. [1691] Application des méthodes de Wallis à la détermination du centre de gravité d'une demi-cycloïde	377
XII.	[1658]. Démonstration d'un théorème de stéréométrie concernant la cubature d'un tronc de cône	379
XIII.	[1659]. Déduction d'un théorème de cyclométrie, basée sur la situation connue du centre de gravité d'un arc cycloïdal	381
XIV.	[1659]. Solution d'un problème d'arithmétique élémentaire	384
XV.	[1659]. Recherches sur la théorie des développées. Développées de l'ellipse et de l'hyperbole. Quadrature d'une courbe du huitième degré à l'aide de la développée de l'hyperbole équilatère. Considérations générales sur la théorie des développées et des courbes parallèles. Développée de la cycloïde	387
	Appendice. Détermination du centre de gravité de la cycloïde, basée sur les propriétés de sa développée	406
XVI.	1659. Construction de la tangente à la quadratrice de Dinostrate	407
CONTRIBUTIONS AUX COMMENTAIRES DE VAN SCHOOTEN SUR LA ‘GEOMETRIA’ DE DESCARTES. ÉDITIONS DE 1649 ET DE 1659. 1649, 1659		406-422
Avertissement		411-415
I.	1649. Cas particulier où la recherche d'un lieu géometrique amène un théorème	416

		Page.
II.	1659. Construction de la normale à la conchoïde	417
III.	1659. Cas particulier des ovales de Descartes où ils deviennent des cercles	419
IV.	1659. Forme de l'ovale de Descartes dans le troisième cas qu'il distingue dans la discussion de ses ovales	420
V.	1659. Mener d'un point donné les normales à une parabole	421
	Appendice. [1654]. Déduction des formules de Descartes pour déterminer le ‘latus transversum’ et le ‘latus rectum’ d'une conique donnée par une équation quelconque du deuxième degré	423
TRAVAUX MATHÉMATIQUES DIVERS DE 1660 à 1666		429-524
Avertissement		431-450
I.	1661. Déduction de la règle pour trouver les logarithmes	451
	Appendice. [1668]. Règle pour trouver les logarithmes	458
II.	1661. Recherches sur la courbe logarithmique	460
	Appendice. [1689]. Détermination du centre de gravité du solide engendré par la révolution de la courbe logarithmique autour de l'asymptote	472
III.	1662. Quadrature de l'hyperbole par les logarithmes. Application à la rectification de la parabole	474
IV.	1662. Relation entre l'altitude et la pression atmosphérique	483
	Appendice I. [1668]. Application aux expériences faites sur l'instigation de Pascal par Perier au Puy de Dôme en Auvergne	491
	Appendice II. 1673. Application à une expérience de Cassini faite sur une montagne près de Toulon	495
V.	[1662]. Construction de l'heptagone régulier	498
VI.	1662. Quadrature de la courbe de Gutschoven et cubature d'un de ses solides de révolution	501
VII.	[1662]. Recherches sur la détermination des tangentes des courbes algébriques	504
VIII.	[1664]. Trouver le diamètre d'une surface sphérique	518
IX.	[1665]. Formules pour passer d'un système de coordonnées cartésiennes à un autre. Application aux cubiques	519
X.	1666. Trouver un nombre qui, divisé par trois nombres donnés, laisse des restes donnés. Application au Cycle Julien	521
XI.	[1666]. Examen d'une rectification approchée de la circonférence du cercle	524

Vorige Volgende