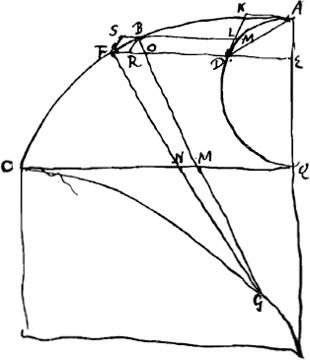
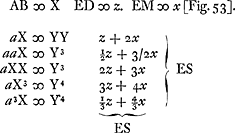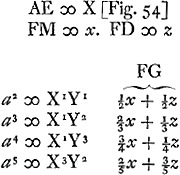§ 2. Sit Cyclois ABC [Fig. 50] vertice A, axe AQ, basi QC. Et a punctis B, F, in curva sumtis, quorum B vertici A propinquius sit, quorumque inter se minima intelligenda est distantia, ducantur rectae BG, FGGa naar voetnoot5), quae conveniant in puncto G; secent vero basin in M et N. sitque FE basi parallela quae secet BG in O. Dico jam FO rectae NM duplam esse, ac proinde et FG duplam GN. Describatur enim super axe AQ semicircumferentia quae secet rectam FE in D, rectam autem SBM, ipsi FE parallelam, in M. et ducatur DK tangens circumferentiae in D quaeque occurrat rectae AK basi parallelae in K. Ipsi vero DK sint parallelae BR, FS, inter parallelas FD, SM interceptae et aequales proinde parti DL quam auferunt eaedem parallelae ab recta DK. Jam quia CN est aequalis arcui DQ ex proprietate cycloidisGa naar voetnoot6), et similiter CM aequalis arcui MQ, erit NM recta aequalis arcui DM. Itaque ostendendum est rectam
| |
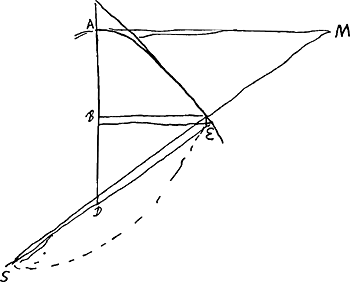
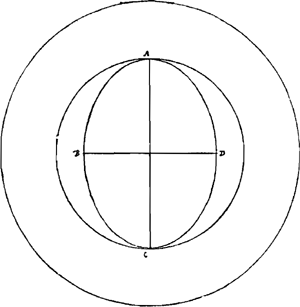
§ 6 Ga naar voetnoot1). ABCD [Fig. 55] est sphaeroides cujus axis AC duplus est potentia diametri ED Ga naar voetnoot2). Dico superficiem sphaeroidis esse ad circulum cujus diameter AC, vel superficiem
[Fig. 55.]
dimidiam sphaeroidis ad maximum in sphaeroide circulum, sicut circulus cum inscripto sibi quadrato ad inscriptum quadratum. sive ut semicircumferentia una cum diametro ad diametrum Ga naar voetnoot3).
Si BD sit semissis AC erit ratio dimidiae superficiei ad circulum BD eadem quae circuli cum inscripto trigono aequilatere ad ipsum trigonumGa naar voetnoot3).
|
-
voetnoot1)
- La Pars Tertia contient de plus des théorèmes sur la quadrature de quelques surfaces courbes quoique ce sujet ne se rapporte que fort indirectement à la théorie mathématique du pendule et que dans le Sommaire de 1660 Huygens n'en fasse pas mention; comparez la note 6 de la p. 119 qui précède. Dans les notes 4-7 de la p. 122 nous avons fait entendre que la grande majorité des morceaux qui se rapportent à la Pars Tertia ont déjà été publiés ailleurs.
-
voetnoot2)
- Les §§ 1-4 qui suivent (la division en §§ est de nous) sont empruntés à un feuillet détaché (Chartae Mathematicae, f. 158-159). Une grande partie de ce feuillet est occupée par un dessin bien exécuté de l'horloge marine avec pendule triangulaire qui date de plusieurs années après 1659 (comparez les figures des p. 19-20 de l'édition originale de l'‘Horologium oscillatorium’, représentant la même horloge vue sous un autre angle, et le texte qui accompagne ces figures). Or, la Fig. 51 qui suit traverse en partie le dessin nommé de sorte qu'elle date de plus tard encore. Néanmoins nous croyons avoir affaire ici à la ‘première application méthodique de la théorie générale des développées’, savoir l'application de 1659 à la cycloïde, dont nous avons dit dans la note 1 de la p. 404 du T. XIV qu'elle ‘est perdue pour nous, puisqu'on ne la retrouve pas dans les manuscrits que nous possédons’. Observons qu'en ce moment le feuillet en question n'avait pas encore été examiné. Les §§ 2-3 ne font évidemment pas partie d'une rédaction soignée (voir la note 5 qui suit); nous supposons plutôt que Huygens, du moins dans le cas du § 3, ait copié, ou reproduit dans une forme peu différente de la forme primitive, une partie de sa démonstration de 1659.
-
voetnoot3)
- Le § 1 n'est qu'un fragment; le début du raisonnement, qui était apparemment un essai de
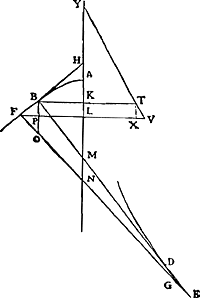
rédaction, fait défaut. La Fig. 49 est une reproduction de la première figure de la Prop. XI de la Pars Tertia de l'‘Hor. osc.’: les lettres du texte correspondent exactement à celles de cette figure, excepté que la courbe DE y est appelée CDE. La courbe FBA est la développante qui correspond à la développée DE. BMG et FNG sont des normales infiniment voisines à la courbe FBA.
-
voetnoot4)
- Il est vrai que la ‘ratio BO ad MN’ est dans la Fig. 49 un rapport entre des lignes verticales, tandis que dans les Fig. 50 et 51 qui suivent la ‘ratio FO: NM’, ou FE: AB, est un rapport entre des lignes horizontales. On pourrait sans doute dans le cas des Fig. 50 et 51, c.à.d. dans le cas de la cycloïde, prendre des éléments verticaux au lieu d'éléments horizontaux (comparez ce qu'en dit Huygens dans l'‘Hor. osc.’ dans la Prop. XI déjà nommée); pourtant il semble probable qu'il désigne ici par ‘haec ratio’ dans le cas spécial de la cycloïde un rapport entre des éléments horizontaux. Comparez sur le § 1 la note 2 de la p. 387 du T. XIV.
-
voetnoot5)
- Les droites BG et FG sont normales à la cycloïde ABC; le fait que Huygens ne mentionne pas cette position normale semble prouver qu'ici il ne s'agit pas encore d'un projet de rédaction destiné au public.
-
voetnoot6)
- Comparez la p. 347 du T. XIV. Dans la Fig. 1 de cette page la droite EK est une normale à la cycloïde; de l'égalité de l'arc GB avec la droite KD dans cette figure, résulte l'égalité de l'arc GD avec la droite AK, c.à.d. dans la Fig. 50 qui nous occupe l'égalité de l'arc DQ avec la droite CN.
-
voetnoot1)
- Le § 2 n'est qu'un fragment. La suite peut avoir été écrite sur une autre feuille; toutefois il est à remarquer que le § 3 peut-être considéré comme une suite du § 2: Huygens a peut-être copié ici le début de sa démonstration originale dans le but de compléter plus tard le § 2 en faisant usage des données du § 3. On lit encore sur la page qui contient le § 3 les seuls mots ‘quia igitur ratio BG...’ qui s'appliquent évidemment à la Fig. 50.
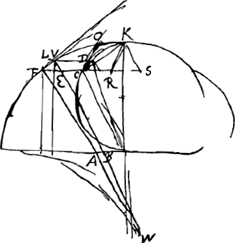
Dans les Fig. 50 et 51 la cycloïde supérieure (développante) est donnée. Il s'agit de démontrer que la développée, obtenue ici comme le lieu des points d'intersection de normales infiniment rapprochées (ou, si l'on veut, des centres de courbure) est également une cycloiïde. Ainsi posé, le problème correspond exactement à celui que Huygens devait résoudre pour déterminer la forme des lames courbées après avoir trouvé que le poids du pendule simple doit décrire une cycloïde afin que les grandes et les petites oscillations aient une même durée. Dans le cas de sa théorie générale des développées c'est également la développée qui est donnée, et en ce sens on peut dire que nous avons affaire ici (note 2 de la p. 142) à la première application méthodique de la théorie des développées et des développantes; quoiqu'il soit peut-être plus exact de dire que le § 3 contient une considération géomtrique se rapportant exclusivement à la cycloïde, considération d'où provint ensuite la théorie générale nommée.
-
voetnoot1)
- Le § 2 n'est qu'un fragment. La suite peut avoir été écrite sur une autre feuille; toutefois il est à remarquer que le § 3 peut-être considéré comme une suite du § 2: Huygens a peut-être copié ici le début de sa démonstration originale dans le but de compléter plus tard le § 2 en faisant usage des données du § 3. On lit encore sur la page qui contient le § 3 les seuls mots ‘quia igitur ratio BG...’ qui s'appliquent évidemment à la Fig. 50.
Dans les Fig. 50 et 51 la cycloïde supérieure (développante) est donnée. Il s'agit de démontrer que la développée, obtenue ici comme le lieu des points d'intersection de normales infiniment rapprochées (ou, si l'on veut, des centres de courbure) est également une cycloiïde. Ainsi posé, le problème correspond exactement à celui que Huygens devait résoudre pour déterminer la forme des lames courbées après avoir trouvé que le poids du pendule simple doit décrire une cycloïde afin que les grandes et les petites oscillations aient une même durée. Dans le cas de sa théorie générale des développées c'est également la développée qui est donnée, et en ce sens on peut dire que nous avons affaire ici (note 2 de la p. 142) à la première application méthodique de la théorie des développées et des développantes; quoiqu'il soit peut-être plus exact de dire que le § 3 contient une considération géométrique se rapportant exclusivement à la cycloïde, considération d'où provint ensuite la théorie générale nommée.
-
voetnoot2)
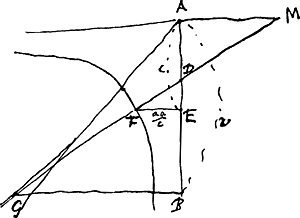
- C'est à dire EF : FV = SC : CK; FV : FL = CK : CO; et EF : FL. La droite FL à peine visible, qui correspond à FS de la Fig. 50, est parallèle à CD. La droite KO (absente) est horizontale.
-
voetnoot2)
- C'est à dire EF : FV = SC : CK; FV : FL = CK : CO; et EF : FL. La droite FL à peine visible, qui correspond à FS de la Fig. 50, est parallèle à CD. La droite KO (absente) est horizontale.
-
voetnoot2)
- C'est à dire EF : FV = SC : CK; FV : FL = CK : CO; et EF : FL. La droite FL à peine visible, qui correspond à FS de la Fig. 50, est parallèle à CD. La droite KO (absente) est horizontale.
-
voetnoot3)
- Huygens a sans doute compris, avant d'en donner une démonstration (voir le § 3 de la p. 397 et le Théor. III de la p. 401 du T. XIV; comparez les Prop. I et IV de la Pars Tertia de l'‘Horologium oscillatorium’) que toute tangente à la développée est une normale à la développante et réciproquement, et que lorsqu'une courbe est normale à toutes les tangentes d'une autre courbe elle en est la développante.
Après avoir trouvé que FW = 2AW (Fig. 51) ou FG = 2NG (Fig. 50) - comparez la note 2 de la p. 404 du T. XIV - il semble s'être servi d'un raisonnement indirect pour démontrer que le lieu des points G (Fig. 50) est une cycloïde. S'il en est vraiment ainsi, le raisonnement dans le cas spécial de la cycloïde se distingue de celui dans le cas de l'ellipse et des autres courbes, tel qu'on le trouve dans le T. XIV. Huygens semble avoir commencé (T. XIV, p. 404) par admettre intuitivement, en considérant la forme du lieu des points G, que ce lieu est une cycloïde (ce que le résultat de la rectification de la cycloïde par Wren rendait probable, ou du moins possible); en adoptant cette hypothèse, il a démontré que les deux cycloïdes de la Fig. 50 (ou de la Fig. 19 du T. XIV) sont dans le rapport d'une développée et d'une développante, d'où l'on peut conclure que le lieu des intersections des normales infiniment voisines à la cycloïde AFC (Fig. 50) est en effet également une cycloïde. Il ne paraît pas probable qu'il se soit servi d'un raisonnement plus direct, puisqu'on n'en trouve pas de traces ni dans les Manuscrits, ni dans l'‘Horologium oscillatorium’.
-
voetnoot1)
- Le § 4 est, croyons-nous, comme les §§ 1-2, un fragment d'une première ébauche d'une rédaction définitive, le § 4 devant faire suite à la démonstration dont le § 3 contient le début non encore rédigé.
-
voetnoot2)
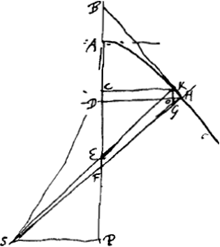
- Comme nous l'avons dit à la p. 207 du T. XIV, le Manuscrit A contient, outre les considérations sur les développées de la cycloïde et des coniques, des calculs incomplets sur les développées des ‘paraboloïdes’, c.à.d. des courbes ya = kxb (note 2 de la p. 475 du T. XVI), ainsi que sur celles des hyperboles de degrés supérieurs, C'est pour rappeler ce fait, et pour faire ressortir l'importance de ces calculs, que nous publions ici le § 5, emprunté aux p. 245, 232 et 234 du Manuscrit nommé. Voir encore sur les développées etc. la fin de la note 2 de la p. 149 et surtout la note 2 de la p. 153 qui suit.
-
voetnoot3)
- En comparant la Fig. 52 avec la Fig. 49 de la note 3 de la p. 143 on voit qu'il s'agit ici de déterminer la forme de la développée de la parabole d'après la methode indiquée dans les §§ 1 de la p. 142 et 4 de la p. 146 et décrite dans la Prop. XI de la Pars Tertia de l'‘Horologium oscillatorium’.
-
voetnoot4)
- Dans le tableau qui accompagne la Fig. 53 Huygens emploie la lettre x d'abord pour indiquer la longueur AB, ensuite pour indiquer la longueur EM; pour éviter la confusion nous avons remplacé le premier x par un X et l' y correspondant par un Y. En comparant ce tableau avec le tableau identique que l'on trouve dans la Prop. XI de la Pars Tertia de l'‘Hor. osc.’ (p. 88 de l'édition originale) on voit qu'en 1659 Huygens était déjà parvenu aux résultats mentionnés dans l'‘Hor. osc.’ sur les ‘paraboloïdes’ ou paraboles de degrés supérieurs.
-
voetnoot5)
- Dans le tableau qui accompagne la Fig. 54 nous avons introduit les lettres X et Y au lieu de x et y pour la raison nommée dans la note précédente. En comparant ce tableau avec celui de la p. 90 de l'édition originale de l'‘Hor. osc.’ on constate qu'en 1659 Huygens avait obtenu les résultats mentionnés dans cet ouvrage sur les hyperboles de degrés supérieurs.
-
voetnoot1)
- Le § 6 est emprunté à une feuille séparée (‘Chartae mathematicae’ f. 55), intitulée: ‘De superficiebus Conoidum et Sphaeroidum’. Elle peut être de 1658 vu que les autres pièces sur la quadrature de l'ellipsoïde de révolution (note 3) datent de cette année.
-
voetnoot1)
- Le § 6 est emprunté à une feuille séparée (‘Chartae mathematicae’ f. 55), intitulée: ‘De superficiebus Conoidum et Sphaeroidum’. Elle peut être de 1658 vu que les autres pièces sur la quadrature de l'ellipsoïde de révolution (note 3) datent de cette année.
-
voetnoot3)
- Ces théorèmes peuvent être considérés comme des cas particuliers du théorème, applicable à un spheroïde ou ellipsoïde de révolution, qu'on trouve aux p. 323 (quatrième alinéa), 335 et 336 du T. XIV; voir aussi la note 5 de la p. 322. Un autre cas particulier y est traité à la p. 323 (cinquième alinéa et note 7).
-
voetnoot3)
- Ces théorèmes peuvent être considérés comme des cas particuliers du théorème, applicable à un spheroïde ou ellipsoïde de révolution, qu'on trouve aux p. 323 (quatrième alinéa), 335 et 336 du T. XIV; voir aussi la note 5 de la p. 322. Un autre cas particulier y est traité à la p. 323 (cinquième alinéa et note 7).
|