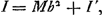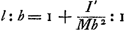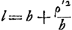Oeuvres complètes. Tome XVIII. L'horloge à pendule 1666-1695

[p. 433]

Appendice VI
À la pars quarta de l'‘Horologium oscillatorium’.
[1692 ou 1693]¹⁾.

[Fig. 160.]

Pendulum pondus cujus centrum gravitatis A [Fig. 160] per Cycloidem delatum AB, acquirit in puncto B infimo celeritatem qua per arcum BD aequalem BA ascendat.

Si vero annulus gravitate praeditus, et tamen ut peripheria simplex consideratus volvatur in paracycloide²⁾ EF, ita ut centrum ejus describat cycloidis portionem AB, is quoque vim collegit, ubi in B pervenit, qua ascendat revolvendo usque in D.

Sed quia in B transiens aequalis motus quantitas est circa centrum in partibus ipsum constituentibus, ac in ijsdem motu horizontali pergentibus per praecedentem¹⁾, necesse est dimidium virium acquisitarum revolutione per EF, cessisse in motum circulationis circa centrum annuli, dimidium vero reliquum in motum horizontalem annuli totius³⁾.

1) La Pièce est empruntée à la p. 171 (numération de Huygens) du Manuscrit H. Les dates du 18 déc. 1692 et du 31 janvier 1693 se trouvent respectivement aux p. 155 et 172. La feuille 169-170 a été enlevée par Huygens qui a noté sur la p. 171: ‘j'ay dechirè icy une feuille’. Celle-ci contenait sans doute des considérations ou des calculs relatifs à la présente Pièce puisque les mots ‘per praecedentem’ du troisième alinéa s'y rapportent évidemment.

2) La paracycloïde est donc une courbe parallèle à la cycloïde, c.à.d. un lieu de points à égales distances d'elle.

1) La Pièce est empruntée à la p. 171 (numération de Huygens) du Manuscrit H. Les dates du 18 déc. 1692 et du 31 janvier 1693 se trouvent respectivement aux p. 155 et 172. La feuille 169-170 a été enlevée par Huygens qui a noté sur la p. 171: ‘j'ay dechirè icy une feuille’. Celle-ci contenait sans doute des considérations ou des calculs relatifs à la présente Pièce puisque les mots ‘per praecedentem’ du troisième alinéa s'y rapportent évidemment.

3) Apparemment Huygens admet ici que pour un corps donné une chute d'une hauteur déterminée de son centre de gravité produit, lorsque tout frottement ou résistance du milieu fait défaut, une quantité déterminée de ‘vires’ quelle que soit le mouvement du corps. La suite fait voir que les ‘vires’ considérées sont pour toute particule du corps proportionnelles au carré de la vitesse. Comparez le passage de 1690 que nous avons cité dans le troisième alinéa de la note 6 de la p. 359 du T. XVI. D'ailleurs Huygens parlait déjà en 1661 de la ‘vis motus’ proportionnelle au carré de la vitesse: voir le troisième alinéa de la p. 376 du T. XVI. Le principe admis ici n'est qu'une forme différente de celui de 1659 (T. XVI, p. 357 et 385-391). La ‘force ascensionelle’ totale du corps doit être telle que lorsque chacune de ses particules s'élève à la plus grande hauteur possible, le centre de gravité de toutes les particules se trouve à la hauteur d'où est descendu le centre de gravité du corps partant du repos.
Huygens commence prudemment par considérer un cas particulier, le plus facile de tous, celui où le corps qui descend en roulant est un cylindre ou plutôt un simple anneau infiniment mince (‘peripheria simplex’). En effet, il n'est pas de toute évidence que la ∑ mv², où v représente la vitesse totale par rapport à la terre (considérée comme immobile) d'une particule de masse m, peut être décomposée en une somme de deux termes dont l'un représente la ‘force vive’, pour nous servir de l'expression de Leibniz (T. XVI, p. 359, note 6) du mouvement progressif et l'autre celle du mouvement de rotation. Voir la note suivante.
Huygens commence par établir qu'au point le plus bas la ‘motus quantitas’ de l'anneau est composée de deux parties égales, correspondant aux deux mouvements nommés. Apparemment il désigne ici par ‘motus quantitas’, contrairement à l'usage ancien (T. XVI, p. 359), la somme ∑ mv² et non pas ∑ mv: pour cette dernière la somme des deux ∑ partielles (elles aussi égales l'une à l'autre) ne donne pas la ∑ totale. La décomposition de la ‘force vive’ en deux parties égales s'étant montrée possible pour le cas de l'anneau roulant, et cela non seulement au point le plus bas mais aussi partout ailleurs, Huygens en tire la conclusion que le mouvement est √2 fois plus lent que lorsqu'il n'est que progressif, ce qui est approximativement le cas lorsque l'anneau est suspendu à un long fil.

[p. 434]

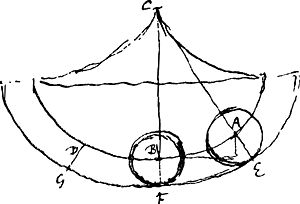
Ergo annulus ad B delatus habet in motu horizontali dimidium virium quas haberet si absque ulla revolutione ex filo pendens venisset: hoc est, habet vires quibus ascendere possit per dimidiam altitudinem arcus AB. Quam ob rem celeritatem horizontalem habebit quee sit ad celeritatem horizontalem descendentis ut pendulum, sicut 1 ad √2, ut notum ex legibus ascensus. Sed ijsdem rationibus in quovis loco portionis ABD ostenditur eandem esse rationem lationis centri ex revolutione acquisitae, ad lationem quem penduli formâ descendens vel ascendens haberet. Ergo tempus totius revolutionis annuli per curvam EG, erit ad tempus vibrationis penduli per arcum AD, quae √2 ad 1, seu proxime quae 7 ad 5.

Propendulo annulo melius accipietur, pondus velut punctum in A centro filo affixum. Nam ipse annulus paulo lentiores vibrationes habebit quam pondus in puncto A collectum, quoniam aliqua particula virium absumpta est in conferendo motu exiguo circa centrum quo radius ex positu AE venit in BF. qui motus juvat rursus in ascensu, quod continuatus conatur disponere radium ex situ BF in DG¹⁾.

1) La décomposition de ∑ mv² en deux parties égales s'applique, dans le cas de l'anneau, à un mouvement progressif ou de translation le long d'une partie infiniment petite de la courbe cycloidale, et à un mouvement de rotation autour du centre de l'anneau. On a généralement, en désignant par v_x la projection de v sur un axe X: est la projection sur le même axe de la vitesse v_o du centre de gravité du corps considéré. En ajoutant les équations de ce genre correspondant à trois axes rectangulaires entre eux, il en résulte c.à.d. la force vive totale - nous pouvons, suivant la pensée de Huygens, considérer comme ‘force vive’ le produit de ∑ mv² par un facteur λ indéterminé, comme nous l'avons fait aux p. 22 et suiv. du T. XVI - est égale à celle du corps considéré comme se mouvant en entier avec la vitesse du centre de gravité + la force vive résultant du mouvement par rapport au centre de gravité. Huygens avait peut-être établi ce théorème général, sans que la forme de sa démonstration lui plût. Peut-être aussi s'était-il borné au cas où tous les points du corps se meuvent parallèlement à un même plan.
Le théorème implique, comme Huygens le dit, que le mouvement roulant de l'anneau est √2 fois plus lent que celui (c'est le cas considéré dans l'Appendice IV qui précède) d'une translation parallèle le long de la courbe cycloïdale. Mais dans le cas de la translation parallèle la ∑ mv² totale reste la même lorsqu'on suppose la masse de l'anneau concentrée en son centre, puisque cette somme ne dépend que de la masse et de la descente du centre de gravité. Or, lorsque le corps est punctiforme on peut tout aussi bien le supposer attaché au fil impondérable de manière à accomplir une oscillation ordinaire, puisque la force vive de la rotation d'un point (comparez la note 2 de la p. 421 qui précède) est négligeable.

[p. 435]

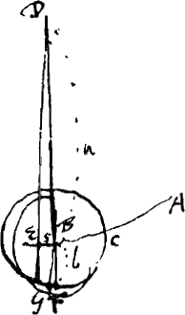[Fig. 161.]

Ut s [Fig. 161] ad sb/a, hoc est ut a ad b ita celeritas motus horizontalis impressus toti simul annuli circumferentiae, ad celeritatem eidem impressam motu circa centrum. ad quos motus imprimendos oportet vires insumi quae sint ut aa ad bb. ac proinde si totae vires descensu arcus acquisitae sint aa + bb erunt insumtae vires in motum horizontalem aa. à quibus et ascensus producitur aa, si totus ascensusad altitudinem arcus sit aa + bb. Hinc celeritas horizontalis annuli in B ad celeritatem penduli simplicis DB ut a ad 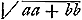. Et rursus longitudo penduli quod sit annulo isochronum erit ad DB ∞ a ut aa + bb ad aa. hoc est ut a + bb/a ad a. Eoque ista longitudo erit a + bb/a. Quod convenit cum nostris de centro oscillationis. Idque hic obiter examinare volui.

Hinc nova demonstratio centrorum oscillationis inveniri potest²⁾.

Voir encore au sujet de cet Appendice la fin de notre aperçu de la ‘Controversia’ à la p. 466 qui suit.

2) En effet, Huygens eût pu démontrer de cette façon la formule générale de la Pars Quarta, non seulement pour l'anneau mais pour un corps quelconque. Dans le cas de l'oscillation ordinaire sans roulement considérée dans l'‘Hor. osc.’ la formule de la note précédente se réduit, après une division par le carré de la vitesse angulaire, à relation déjà considérée à la p. 47 de l'Avertissement. Remarquons que b désigne ici la distance du point de suspension au centre de gravité, laquelle est appelée a dans la Fig. 161. La force vive totale est proportionnelle à I. Elle se compose de la force vive, proportionnelle à Mb², de la translation du corps concentré en son centre de gravité et de la force vive, proportionnelle à I′, de la rotation du corps autour de ce centre. La force vive totale du mouvement est par conséquent à la force vive de la translation dans le rapport I : Mb² ou 1 + I′/Mb² : 1. Comme dans le cas de l'anneau, le pendule quelconque considéré se meut donc plus lentement que si son poids était concentré en son centre de gravité, auquel cas la force vive totale - comparez la fin de la note 1 - serait une force de translation. Le carré de la période du pendule réel est à celui de la période du pendule simple sictif de longueur b comme 1 + I′/Mb² : 1. Il en résulte que la longueur l du pendule simple isochrone avec le pendule réel est à b dans ce même rapport.
Lorsqu'on prend I′ = Mρ′², la proportion se réduit à , conformément à la formule de la p. 48 de l'Avertissement.