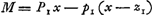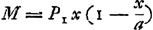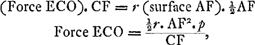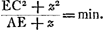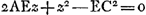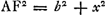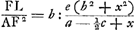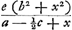Oeuvres complètes. Tome XIX. Mécanique théorique et physique 1666-1695
(1937)–Christiaan Huygens–
[pagina 69]
| |
VIII.
| |
[pagina 70]
| |
 [Fig. 46.]
VIII, § 3Ga naar voetnoot3). Donnè dans l'assemblee le 15 fevrier [1672?], mais la construction 2 ou 3 mois devant.
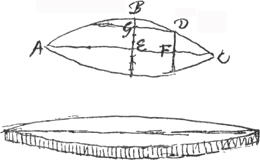
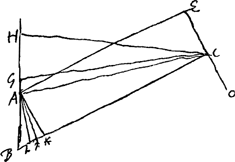
Problema. Sit trabs vel cylindrus muro obliquè infixus [Fig. 47) cujus sectio per axem, facta plano ad muri superficiem recto, sit trapezium ABCE; sectio superficiei muri recta BAH. Trahente autem potentia secundum rectam ECO, lateribus cylindri perpendicularem, donec cylindrus rumpatur, oporteat invenire secundum quam sectionem ejus fiet fractio. Cylindri ipsius nulla gravitas consideratur. Junctâ CA, sumatur ei aequalis CF. Dico cylindrum ruptum iri secundum sectionem AF, factam nimirum plano ad planum ABCE recto. Hoc autem constabit si ostensum fuerit minori potentia trahente per ECO opus esse ad fractionem secundum sectionem AF quam secundum aliam quamcunque. | |
[pagina 71]
| |
Ponatur potentia minima quae directe trahendoGa naar voetnoot4) rumpere possit cylindrum secundum sectionem AB, referri rectâ BC. Et ducatur CG ita ut angulus CGB fiat aequalis angulo AFB. Erunt ergo triangula BCG, BAF similia. ac proinde ut BA ad AF, hoc est ut sectio secundum BA ad sectionem secundum AF, ita erit BC ad CG. Unde quum BC sit potentia directè rumpens secundum sectionem AB, erit CG potentia directe rumpens secundum sectionem AF. Ducatur rursus CH ita ut fiat angulus GCH aequalis angulo FCA. Erunt ergo triangula similia GCH, FCA, quia et angulos ad G et F aequales habent ex constructione. Est igitur ut CF ad FA ita CG ad GH. Sicut CF ad ½FA, ac proinde etiam ut CG ad ½GH, ita est potentia directè rumpens secundum sectionem AF ad potentiam quae ibidem rumpat cylindrum trahendo secundum ECO ex GalileoGa naar voetnoot5). Ergo cum CG sit potentia directe rumpens secundum AF, erit ½GH potentia quae trahendo per ECO rumpat secundum eandem sectionem AF. Rectam vero GH hac constructione inventam minorem esse quam si sectio cylindri facta per A non fecisset triangulum ACF isosceles, facile perspicitur; cum tunc etiam triangulum HCG non fuerit isosceles futurum. ideoque basis ejus GH major quam nunc est, quoniam angulus ad verticem C magnitudine datus est quippe aequalis angulo ACF. Omnium itaque sectionum per A factarum ea quae minimâ potentiâ rumpitur per ECO trahendo, est sectio AF. Quod si vero alia quaepiam sectio intelligatur parallela alicui earum quae per A fieri possunt certum est eam quae fit per A minori potentia rumpi, quippe cujus punctum infimum quod hypomochlij viceGa naar voetnoot6) est magis distet a puncto C. Itaque omnium facillima ruptura erit secundum sectionem per AF. quod erat ostendendum. Inventa AF ut supra, si ducantur utrinque rectae AL, AK quae cum ipsa AF aequa- | |
[pagina 72]
| |
les angulos constituant, eadem potentia trahente per ECO opus erit ad rumpendum cylindrum secundum alterutram sectionum quae secundum AL vel AK, quia tunc triangulum GCH eadem qua supra constructione effectum, utraque positione angulos H et G ad basin eosdem habebit, nimirum quia triangulum hoc simile erit alterutri triangulorum ACK, LCA, quae similia esse inter se manifestum est. Idcirco autem et basis utrobique eadem erit magnitudo, cujus semissis designat potentiam quae per ECO trahens ruptura sit cylindrum secundum sectionem propositam AL vel AKGa naar voetnoot1). 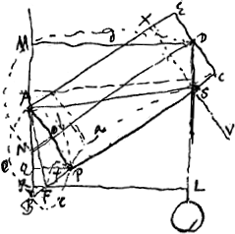 [Fig. 47.]
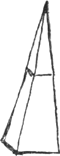
VIII, § 4. Ubi rumpetur si pondus pendeat ex D medio EF [Fig. 47], trahatque secundum DL muro MB parallelam. 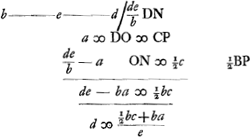 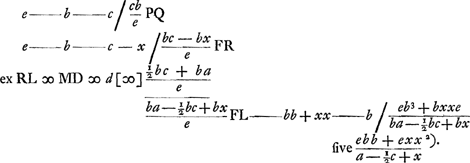 | |
[pagina 73]
| |
Ergo per regulam de max. et min.Ga naar voetnoot3)
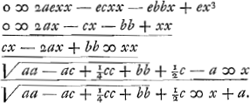
Sumatur CS ∞ ½PB, erit PS ∞ a - ½c, et qu. SA ∞ aa - ac + ¼cc + bb. | |
[pagina 74]
| |
Sit SF ∞ SA, eritque jam 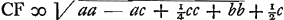 , hoc est ∞ x + a. Ergo PF ∞ x quaesita. , hoc est ∞ x + a. Ergo PF ∞ x quaesita.
Ergo sumta SC ∞ ½PB, fit ∆ SAF isosceles. quale fuisset si trabem SXAB traxissem secundum SV. adeo ut appareat nihil referre an secundum SV an SL trahatur, quod sane ab initio animadvertere debueramGa naar voetnoot1). 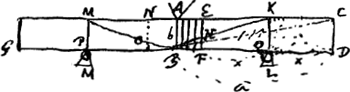 [Fig. 48.]
VIII, § 5Ga naar voetnoot2). Trabs rectangula vel lapis potius earn formam habens GC [Fig. 48]. Quaeritur ubi supponenda duo fulcra MLGa naar voetnoot3) quibus ita sustineatur ut non magis periculi sit rumpi in medio AB quam in KQ vel MP, quibus locis fulcra statuantur. Sint portiones KF, PN singulae aequales KD vel MG. Et jungantur BK, BM. Itaque portio KD aequilibris KF; ideo haec nihil ponderat ad rumpendum solidum secundum AB, sed tantum particula EFBA; et ab altera parte particula similis BN. Sed particulae EFBA segmentum quidem tenue AB tota sua gravitate premit B medium fulcrorum LM, segmentum vero EF premit idem medium B ac si tantum EH suspensum esset ex B, quia diminuitur momentum prout accedit ad KQ. Atque ita tota portio AF ac si trapezium ABHE penderet ex B. Eadem vero est vis pendentibus ABHE, ABON ex B ad rumpendum AB juncturam, ac si cuneus A tanto pondere incumberet trabi MKQP quam sine pondere considero. Et hoc rursus idem est ac si conversa figura | |
[pagina 75]
| |
penderet trabs eadem super cuneo A, trahereturque in punctis K et M a trapezijs singulis ABHE, ABON. Hic vero jam ut aequale periculum sit rupturae in AB, ac in KL ob pondus portionis KD, oportet trapezium ABHE ductum in distantiam AK aequari portioni KD ductae in dimidiam distantiam KC, quia idem habet momentum ac si tota portio penderet ex centro gravitatis suae. Haec sunt calculi fundamenta.
Intelligatur rigida prorsus trabs sive lapis GC. Jam si KD sufficit ad rumpendum in KL, etiam KF sufficit ad efficiendam rupturam in eadem KL. Itaque quaeritur rectè quanta debeat esse portio NF ad faciendam rupturam in AB. Nam hanc nihil impedient jam juncturae KQ, MP. quippe aliunde abrumpendae. 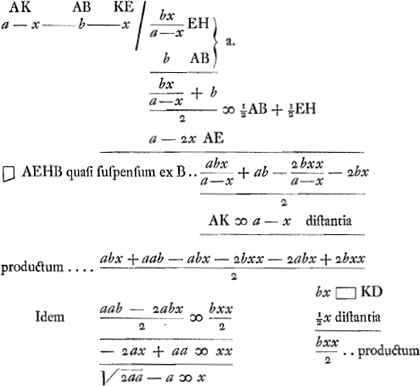 Parallelepipeda ex metallo hoc modo fulcris imposita clariorem quam omni alio positu sonum edunt ..... Etc. Comme cette remarque et quelques-unes qui suivent ne se rapportent pas à la statique, mais à la théorie des vibrations et du son, nous ne les publions pas ici. On les trouvera à la p. 368 qui suit. |
|