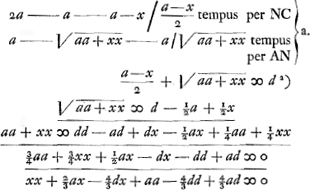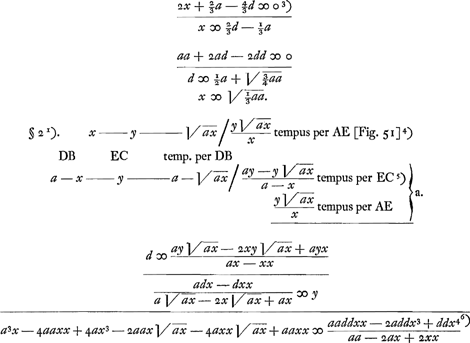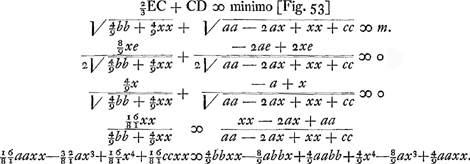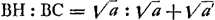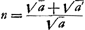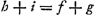Oeuvres complètes. Tome XIX. Mécanique théorique et physique 1666-1695

[p. 98]

III.
Chute brachistochrone le long d'une droite brisée.

[Fig. 50.]

[Fig. 51.]

§ 1¹⁾. CB [Fig. 50] horizontalis aequalis AB perpendiculari. Inclinandum ab A est planum AN, ut descensus gravis per AN et cursus continuatus per NC sit omnium brevissimus.

²⁾

1) Manuscrit C, p. 240, datant de 1668. Huygens s'est apparemment posé la question de la chute brachistochrone de A en C. Ne se voyant pas en état de calculer la forme de la courbe brachystochrone - qui ne fut trouvée que peu après sa mort - il se borne aux cas considérés dans les Fig. 50 et 51. Le § 2, où le calcul conduit à une formule assez longue, est dans le Manuscrit antérieur au § 1: dans le cas plus simple du § 1 Huygens peut achever le calcul.

2) Dans la première de ces trois formules 2a représente la longueur du chemin parcouru par un corps se mouvant uniformément avec la vitesse acquise par une chute le long de AB ou de AN durant un temps égal à celui d'une chute accélérée le long de AB; l'unité de temps est choisie de telle manière que le temps nommé est représenté par a. La deuxième équation exprime que les temps nécessaires pour parcourir AB et AN d'un mouvement accéléré sont entre eux comme ces deux longueurs (Horologium oscillatorium, Pars Secunda, Prop. VII). Par conséquent d est le temps total du mouvement ANC.

[p. 99]

^3)4)5)6)

3) C'est la condition pour que le temps d, qui figure dans l'équation précédente, ait une valeur minimale (ou maximale), ce qui est trouvé en remplaçant x par x + e (e étant une quantité infiniment petite) dans l'expression précédente qui doit alors garder la même valeur: comparez le § 3. Huygens a aussi pu se servir de la méthode de Hudde (§ 3) qui d'ailleurs revient à peu près au même.

4) Comparez la note 2. Le temps d'une chute accélérée AD est √ax lorsque le temps de la chute accélérée AB est a.

5) La proportionnalité des temps correspondant aux chutes accélérées DB et EC avec les longueurs de ces droites - comparez la note 2 - subsiste lorsque les vitesses initiales égales ne sont pas nulles.

6) Comme dans le cas plus simple du § 1, il faudrait examiner pour quelle valeur de x le temps d acquiert une valeur minimale.

[p. 100]

[Fig. 52.]

[Fig. 53.]

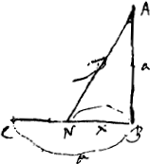
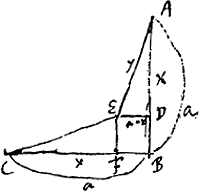
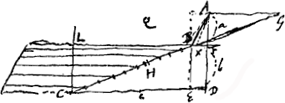
§ 3¹⁾. Dato puncto C et altiori A [Fig. 52], et plano horizontali BL, invenire in eo punctum B, ut per inclinata plana AB, BC fiat descensus tempore brevissimo.

Si AF designet tempus per AF, etiam AB designabit tempus per AB, et GB tempus per GB. Et sumpta GH media proportionali inter GB, GC²⁾, designabit BH tempus per BC. Ergo fit BH pars proportionalis ipsius BC³⁾. Ideoque problema eodem redit, ac si LF esset superficies vitri positi à parte Q et aëris à parte H, et quaeratur punctum refractionis B, quia AB cum parte proportionali BC debet esse brevissima⁴⁾.

CD ∞ c, AF ∞ a, FD ∞ b, BF ∞ x. minima linea e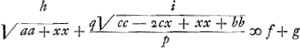



hoc est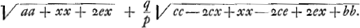

Hoc h + i esset aequandum alicui maximo m secundum methodum Huddenij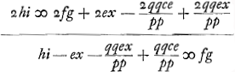⁵⁾.

⁶⁾

Huygens porte ces expressions au carré en négligeant les termes qui contiennent e². Il en tire une valeur de hi, qu'on peut égaler au produit des deux expressions h et i trouvées plus haut. Il en conclut: erit aequatio sextae potestatis x.

Per aequationem differentialem operando, fit aequatio quartae potestatis x, ut in charta adjuncta⁷⁾.

1) Manuscrit G, f. 54, datant de 1690 (les f. 53 et 55 portent respectivement les dates du 27 août et du 4 sept. 1690).

2) GH représente donc le temps d'une chute accélérée le long de GC.

3) Lorsqu'on a GB : GC = a : a′, il en résulte . Dans la Fig. 52 a′ est désignée par a + b.

4) En effet, suivant Fermat - dont le calcul confirme la loi des sinus de Snellius ou de Descartes; comparez les p. 266, 267 et 340 du T. XVII - un rayon, partant du point A, est rompu en un point B tel, que le temps total nécessaire pour atteindre l'oeil C est minimum. Il faut donc que AB + BC/n soit minimum, n étant l'indice de réfraction, c.à.d. suivant Fermat le rapport de la vitesse du rayon dans l'air à celle dans le verre. Or, lorsqu'on prend - ou bien n = p/q, comme Huygens écrit un peu plus loin - la condition revient à rendre la somme AB + BH aussi petite que possible, laquelle somme représente le temps que met le mobile ici considéré par Huygens à parcourir AB et BC d'un mouvement accéléré.

5) La méthode de Hudde (‘Joh. Huddenii Epistola secunda’ de 1658 ‘de Maximis et Minimis’, p. 507 et suiv. de ‘R. Descartes Geometria, editio tertia’ de 1683, avec commentaires de F. van Schooten etc.) est basée sur le fait qu'une expression (algébrique) à une variable étant égalée à une quantité déterminée différant fort peu de la valeur maximale ou minimale de l'expression, cette équation possède deux racines à fort peu près égales. Dans le cas où l'expression contient des radicaux la méthode ne diffère pas de celle dont Huygens se sert ici.

6) Puisqu'il résulte de , que .

7) Leibniz emploie l'expression ‘equation differentiale’ - dont il se servait, lui le premier, depuis plusieurs années - dans sa lettre à Huygens du 25 juillet 1690 (T. IX, p. 451). La présente remarque fut d'ailleurs ajoutée plus tard, semble-t-il. Nous ne reproduisons pas la ‘charta adjuncta’ (qui est devenue la f. 219 des ‘Chartae mathematicae’): le calcul qui suit (§ 4) en tient lieu.

[p. 101]

§ 4⁸⁾.

⁹⁾

8) Manuscrit G, f. 65, datant de 1690 (les f. 59 et 78 portent les dates du 25 sept. 1690 et du 1 janvier 1691). Dans la Fig. 53 ECD est un rayon de lumière réfracté en C. Il s'agit de trouver le point C, lorsque E et D sont donnés. Comparez les notes 4 et 7. Dans le § 4 Huygens donne à l'indice de réfraction n, correspondant à P/q du § 3, la valeur particulière ⅔. Dans la ‘charta adjuncta’ (note précédente) il conservait la valeur générale P/q.

9) e est un accroissement infiniment petit de x, donc, comme Huygens le dit au § 3, une ‘minima linea’.