Oeuvres complètes. Tome XIX. Mécanique théorique et physique 1666-1695

[p. 418]

IV.
Recherche du point où deux rayons incidents infiniment voisins situés dans un même plan normal à la surface d'un milieu réfringent ordinaire se coupent dans ce milieu.
[1676 ou 1677.]¹⁾

[Fig. 140.]
OS est normale à AE.

§ 1. [Rayons convergents tombant sur une surface plane].

Les rayons sortent du verre et se coupent dans l'air.

Cum sit PA ad AE ut 3 ad 2 [Fig. 140], itemque PD ad DF ut 3 ad 2, differentia duarum PA, PD debet esse 3/2 differentiae duarum EA, DF. hoc est AB ∞ 3/2 AC - 3/2 GF. AC est 3/2 AB²⁾.

AS ∞ m, SE ∞ n, CH ∞ x, CG³⁾ ∞ a, AC ∞ b. Ratio AC ad GF componitur ex rationibus x⫟a-x hoc est CD ad GE et m ⫟ n.

1) Manuscrit E, p. 81. Comparez sur la date la note 1 de la p. 416.

2) C'est ce qu'on voit immédiatement d'après la construction des ondes [Fig. 130]: AC est le chemin parcouru dans l'air par le rayon réfracté, tandis qu'un rayon incident parallèle qui passe par D parcourt dans le verre une longueur égale à AB.

3) Ou plutôt CE, puisque CG est une droite brisée. On peut d'ailleurs également écrire AE = a, comme Huygens le fait un peu plus loin, puisque AC et GF sont infiniment petites. De même x = AH.

[p. 419]

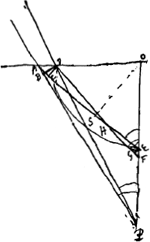
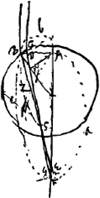[Fig. 141.]

Le lieu des points H est une diacaustique. Voyez sur une catacaustique la p. 399 [datant de 1678] du T. XVIII.

§ 2. [Rayons parallèles tombant sur un cylindre ou une sphère]. Les rayons viennent de l'air et se coupent dans le verre.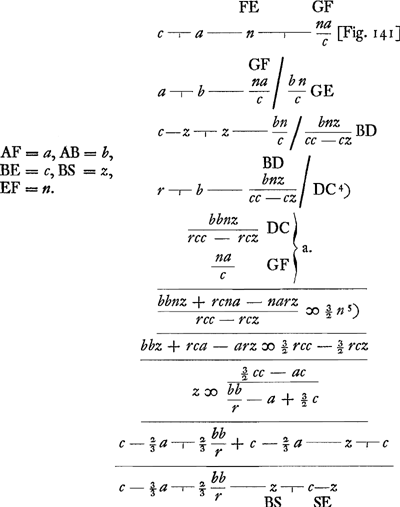

⁴⁾⁵⁾

4) La longueur r n'est apparemment pas une longueur donnée dans la figure. On peut la construire d'après l'équation du texte en formant un triangle rectangle BAM ou PQB semblable au triangle

CDB [Fig. 141 bis ou 141 ter]. Dans ces figures AM et BQ = r. Mais Huygens ne considère sans doute que le cas où les deux rayons sont fort proches de l'axe AF. On peut alors considérer BD comme horizontale et faisant partie de BA, tandis que CD est à peu près égale à la distance de A au sommet. Alors r est le rayon de la sphère, puisque l'égalité BD , où r est ce rayon, conduit à l'équation du texte CD.r = BD.b.

5) L'égalité se démontre en soustrayant l'une de l'autre les équations 2 BE = 3 (distance de E au centre de la circonférence) et 2 CF = 3 (distance de F au même centre), lesquelles expriment pour les deux rayons la loi des sinus.