Oeuvres complètes. Tome XIX. Mécanique théorique et physique 1666-1695

[p. 424]

VI.
Ovale de descartes en verre, servant à réunir en un point intérieur tous les rayons issus d'un point de l'axe qui tombent sur lui.
[1676 ou 1677; 1678]¹⁾

[Fig. 148.]

²⁾³⁾

En effet, comme dans le cas considéré au § 4 de la Pièce V, la ‘curva omnium undarum particularium tangens communis’ doit se réduire en G en un seul point, de sorte que tous les rayons employent le même temps pour parvenir de F en G. Comparez aussi la Pièce X qui suit.

1) Manuscrit E, p. 76 et 77 (§ 1) et p. 84 (§ 2). Comparez sur les dates la note 1 de la p. 416. Il s'agit de la première ovale de Descartes (‘Géométrie’, livre II).

2) Huygens ne considère ici que ce cas spécial. Il aurait évidemment tout aussi bien pu prendre des longueurs FA et AG quelconques, comme il le fera dans le Chap. VI du Traité de la Lumière.

3) On voit déjà ici, et dans la figure, que Huygens cherche une construction mécanique de la courbe.

[p. 425]

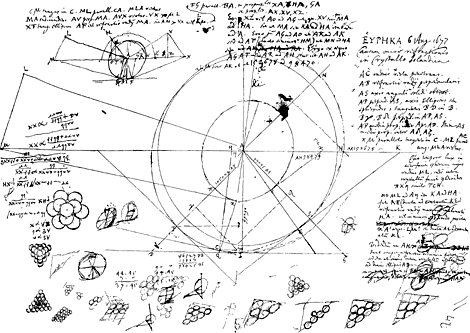
§ 2. CGFA [Fig. 149] funiculus ligatus ad stylum C et ad angulum A gnomonis FAC. Regula GCL mobilis circum G. Angulus CFL mobilis circum F. Stylus C est in puncto communi regulae GCP, FC et AC. Angulus CFL ejusmodi ut sit CF ad FA ut 3 ad 2. fiet curva NC quae radios ab F venientes colligit ad G. Nam semper erunt 2/3 FC + CG ∞ CG + FA quia semper eadem longitudo funiculi, ablatâ GF⁴⁾.

Il est évident que par une rotation de l'ovale autour de l'axe FG on obtient un corps pouvant servir à réunir en un point un faisceau de rayons incidents.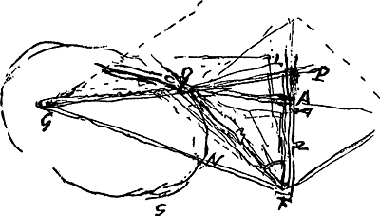

[Fig. 149.]

§ 2. 24 Mart. 1678. Ducatur CN [Fig. 150] tangens arcum CX in C. deinde CL ut sit MC ad LN ut 3 ad 2. Jam CL erit tangens in C, ut postea ostendetur. unde γβ perpendicularis CL secabit curvam ad angulos rectos. Estque angulus γCM aequalis CLM, cum utrivis addendo MCL efficitur angulus rectus. Item angulus βCB aequalis est LCN cum utrivis additus βCN efficiat rectum. Ergo ut sinus anguli CLM ad sinum anguli LCN, hoc est ut CM ad LN, hoc est ut 3 ad 2, ita sinus anguli γCM ad sinum anguli βCB. unde radij incidentis AC refractio intra diaphanum DC erit CB.

Jam quod dictum est CL tangere curvam in C sic ostendetur. Si non tangit, secet in S ut sit recta linea LSC, ac primo cadat S inter C et D. Et ducantur SA, SB, se-

4) AC doit être une règle mobile de manière que le triangle CAF garde sa forme, en d'autres termes CA peut par hypothèse se mouvoir parallèlement à elle-même par rapport au plan du triangle, lequel tourne autour du point fixe F. De cette façon la somme AF + FG + CG peut toujours être égale à la longueur de la corde et, puisque FG est invariable, il en sera de même de la somme AF + CG ou 2/3 CF + CG. On aura donc FC + 3/2 CG = const. comme il convient.

[p. 426]

cantes arcus DT, CX in Q et φ. Et sint SO, SH perpendiculares in AC, CN. Denique centro A describatur arcus SV. Et centro B arcus SZ. Jam apparet propter quadrilatera similia MLNC, OSHC, esse ut MC ad LN ita OC ad SH. Ergo et OC ad SH ut 3 ad 2. Sed quia ex proprietate curvae etiam TC ad DX ut 3 ad 2, atque ita etiam QS seu TV ad DZ, erit et VC ad ZX sive Sφ ut 3 ad 2. Ergo VC ad Sφ ut OC ad SH, quod est absurdum, nam OC apparet majorem esse quam VC. et SH minor ostenditur quam Sφ. Est enim SH minor quam SY quia angulus SHY est rectus. Et SY minor quem Sφ quia BY major quam Bφ sive BC, ob angulum rectum BCY. Unde SH omnino minor erit quam Sφ, ut dicebamus.

Quod si S distet ultra C a vertice D, eadem est praeparatio ac demonstratio, nisi quod jam OC minor fit quam CV, et SH major ostenditur quam Sφ, quod scilicet SH sit major quam Sψ et haec major quam Sφ, quae est brevissima quae à puncto S ad arcum XC duci queat.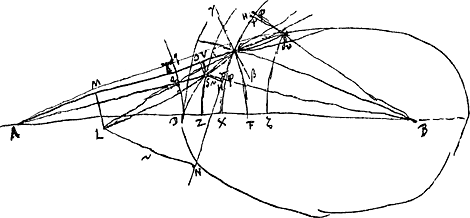

[Fig. 150.]

[p. *7-*8]