Oeuvres complètes. Tome XIX. Mécanique théorique et physique 1666-1695

[p. 544]

Appendice III
Au traité de la lumière¹⁾.

[Je dis de plus, si ces corpuscules estoient collez²⁾] legerement ensemble, qu'en rompant cette pyramide [Fig. 210 de la p. 519] elle se casseroit suivant des faces paralleles a l'une des trois qui font sa pointe, et par là, comme il est aisé de voir, elle produiroit des rhomboides semblables a ceux du mesme cristal. Et la raison est qu'en ses cassant suivant les dits plans, chaque spheroide ne se detache que de deux spheroides³⁾ de la couche voisine, mais si quelque spheroide de ces couches contigues vouloit en sortir pour s'attacher a celle qui se separe, il faudroit qu'il se detachast de six autres spheroides de sa couche qui le tienent serrè, dont les quatre le pressent sur ses surfaces applaties. Il est vray que la rupture se pourroit encore faire suivant des plans paralleles a la base de la pyramide, en detachant chaque spheroide de 3 autres qu'il touche de la couche voisine, mais parce que dans ces couches les spheroides ne sont pas pressez par ceux qui leur sont contigus dans la mesme couche, ils adherent facilement a la couche qui se detache, et font ainsi que toutes deux se trouvent inegales et rabotteuses.

Bartholin rapporte que ce cristal se trouve parfois de figure pyramidale triangulaire. car apres avoir dit que la figure ordinaire est rhomboide, il adjoute, excepto aliquo casu, ubi trigonicam pyramidalem figuram nativum exhibuit solum⁴⁾. Mais, sans supposer de pyramide, si l'on concoit seulement une masse composée de tels petits spheroides rangez suivant la maniere la plus naturelle, c'est a dire qui les unit en sorte qu'ils soient les plus serrez qu'ils puissent estre; cette masse en se cassant produira encore les mesmes figures rhomboides, parce que l'arrangement est de la mesme maniere que dans la composition pyramidale, c'est a dire que dans la premiere couche les spheroides sont rangez comme dans cette figure [Fig. 229]. Dans la seconde qui est par dessus celle-cy, les centres des spheroides sont au dessus des points qui sont icy marquez. Puis dans la troisieme couche les centres des spheroides sont au dessus des 0 0.

1) Physica varia, f. 97. C'est la seule feuille qui nous reste de ce qui était, semble-t-il, la première rédaction des remarques sur la constitution des cristaux, insérées en partie dans le Traité de la Lumière. Comparez la p. 382 de l'Avertissement qui précède.

2) Comparez la l. 16 de la p. 519 qui précède.

3) Trois sphéroïdes, d'après la l. 22 de la p. 519.

4) P. 3 de l'ouvrage cité à la p. 408 qui précède.

[p. 545]

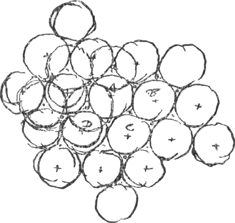[Fig. 229.]

Et à la quatrieme les centres sont au dessus des + +, c'est a dire directement au dessus des centres de la premiere rangée. A la cinquieme au dessus des points ou centres de la seconde rangee, et ainsi consecutivement. Ou il est a remarquer pourquoy la troisieme couche pose plustost ses centres au dessus des 0 0, qu'au dessus des + +, car l'un paroit aussi naturel que l'autre. Et toutefois cela confondroit tout l'arrangement dont nous avons icy besoin. Mais il y a cette raison, que les spheroides de la 3^e couche ou estage se mettant au dessus des 0 0, ils appuient sur les spheroides du second estage en sorte que ceux cy leur obeissent un peu en se balançant sur deux points de leur contact. Au lieu que ces mesmes spheroides du 3^e estage se voulant mettre au dessus des + +, ils ne trouvent point ceux du deuxieme estage disposez a leur obeir parce qu'ils les pressent justement au dessus du point ou ils appuient sur ceux du premier estage de sorte que chaque spheroide du troisieme estage demeure plustost sur les 3 spheroides du second ou il trouve pour ainsi dire plus de creux. Mais cecy se conçoit bien mieux en bastissant ces estages avec des spheroides effectifs qu'a se l'imaginer sur la figure⁵⁾.

Or les raisons qui peuvent faire croire que le cristal d'Islande est composè de petits corpuscules ainsi formez et arrangez, sont premierement, qu'il se fend de mesme dans trois sens differents, et que les faces en devienent polies et inclinees des mesmes angles que celles de nostre amas des spheroides. Secondement qu'en froissant des pieces peu espaisses de ce cristal entre des tenailles a vis ou autrement, l'on y apperçoit des fentes droites dans le sens des costez de la base de la pyramide cy devant representée, ou bien dans le sens de la ligne MN dans la figure rhomboide⁶⁾. Et en troisieme lieu, qu'en usant le cristal sur une pierre rude l'on trouve beaucoup plus de facilitè en le faisant par la pointe comprise des trois angles plans obtus et egaux que par quelqu'autre des pointes, ou en quelqu'autre sens que ce soit. Ce qui vient de ce qu'en ce sens, qui est celuy des plans paralleles a la base de la pyramide, les petits spheroides ne sont pas retenus par ceux de leur couche qui les environnent, comme nous avons desia remarquè auparavant. Et par la mesme raison ce cristal est plus difficile a

5) Ce passage fait voir que Huygens a construit des modèles de cristaux.

6) La figure fait défaut.

[p. 546]

polir suivant ces plans que dans toutes les autres sections. Ce qu'il y a de difficile a penetrer c'est d'ou peuvent estre engendreés ces petits spheroides egaux et de cette forme qui est telle fort pres et peut estre exactement que le quarrè du grand diametre est octuple du quarrè de l'axe. Pour l'arrangement j'en ay apportè quelque raison, quoy qu'il ne soit pas assè de comprendre d'ou vient la premiere couche platte de ces spheroides. Pour en faire la recherche il faudroit examiner les lames plattes de glace qui se forment dans l'eau quand elle commence a se geler⁷⁾, comme encore la generation du sel marin et d'autres sortes de cristal de roche, ou il y a aussi par tout des surfaces plattes. Et quant a la figure cubique du sel marin, elle peut venir d'une composition pareille a celle des rhomboides du cristal d'Islande parce qu' au lieu des rhomboides ce seroient des cubes, si les spheroides avoient leur grand diametre a leur axe &c. Voir a la fin de la page suivante.

7) Comparez la l. 5 de la p. 519 qui précède.