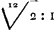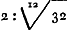Oeuvres complètes. Tome XX. Musique et mathématique
(1940)–Christiaan Huygens–
[pagina 30]
| ||||||||
A. Origine du chant. Rapport des longueurs des cordes consonantes suivant Pythagore, etc.§ 1Ga naar voetnoot1). L'origine du chant vient des consonances, je dis du chant d'une seule voix ou instrument, aussi bien que de celuy à plusieurs voix dont on use aujourd'huy. Car ce plaisir que l'on prend d'entendre les consonances n'est pas seulement à l'egard de deux sons consonants en mesme temps, mais il y en a tout de mesme a entendre ces tons les uns apres les autres. Et comme l'oreille est offensée par la dissonance de deux sons entendus a la fois, ainsi l'est elle encore par ces mesmes sons proferez de suite, quoyque la rudesse ne soit pas tout a fait si grande. Ce qui donc a fait que les hommes par toute la terre chantent par les mesmes intervalles ce n'est pas un hazard, ni une chose fort estrange, mais tous ces intervalles ont estè reglez par les consonances, et la musique devant donner du plaisir et non du chagrin elle ne pouvoit se chanter par d'autres intervalles que ceux là.
§ 2. Quand on chante V R M F S L C V2Ga naar voetnoot2) il y a les tons de V M F S L V2 qui font tous des consonances contre le premier V. Et plusieurs encore entre eux. Et cela fait premierement que l'oreille se plait a entendre ceux la les uns apres les autres qui font consonance avec celuy qui a immediatement precedè comme V M S V2 F L V2 S V. Secondement elle aime encore a entendre les uns apres les autres, quand bien elles ne consonent pas avec les precedentes immediatement, mais avec les penultiemes ou mesme d'autres anterieures sur tout quand elles ont fait quelque impression. Ainsi en chantant V S F M F S L S S V le troisieme ton de F fait un bon effect parce qu'il fait consonance avec le premier V. et le 4e M contre S et V precedents; et le F suivant contre le F precedent (car l'unison tient en cecy lieu de consonance) et contre le V. le second S contre les precedents MSV. et le L contre FMV. Or les premiers sons de musique doivent avoir estè ceux qui faisoient ensemble les | ||||||||
[pagina 31]
| ||||||||
plus remarquables consonances comme l'octave la quinte et la quarte. ainsi VFSV2 et cela se voit en effect de ce que les premieres Lyres n'ont eu que ces quatre chordes, et que toute l'antiquitè n'a reconnu que ces premieres consonancesGa naar voetnoot3). En suite la quinte du S au R vers en haut ou la quarte de S vers en bas ont montrè les tons du R, et la 5te de R L le L. et la quarte vers en bas LM le M et depuis M la quinte vers en haut le C. Et voila tous les tons de l'octave par ou la voix monte en chantant. Ces tons ayant cette origine cela a estè cause en partie que les anciens n'ont pas considerè que les tierces majeure et mineure et les 6tes estoient des consonances. Lesquelles quoyque mesconnues n'ont pas laissè d'estre emploiees dans leur chant de sons consecutifs, aussi bien que dans celuy d'aujourdhuy. Il est vray que c'est une chose assez estrange de ce qu'ils ne trouvoient pas que les chordes distantes par ces intervalles de tierces et sixtes faisoient un son agreable aussi bien que les quintes et les 4tes et que la ou l'on ne fait point d'accords ou il n'entre de 3 ou de 6, dans leur siecle on ne trouvoit pas qu'elles meritassent le nom de consonances. Mais nous parlerons apres de la cause de cecyGa naar voetnoot4). Quant a l'origine des semitons c'est a dire des autres tons que nous chantons quelquefois et qui sont differens des precedents, il estoit necessaire que le C♭Ga naar voetnoot5) fust trouvè le premier a cause qu'on trouvoit qu'en montant de F jusqu'au C cela faisoit mauvais effect lors que l'impression de F restoit dans l'oreille qui ne consonne point avec C, et seulement contre le SGa naar voetnoot6), qui mesme pouvoit n'avoir pas precedè. Mais de monter par FSLC♭ estoit beaucoup plus agreable parce que le C♭ est consonante au S et au F, avec lequel il fait la 4e. qui estoit un des intervalles les premiers connus, ce qui a fait trouver aisement ce son de C♭. Les autres sons qu'on appelle chromatiques peuvent avoir estè trouvè par les cadences aux endroits ou il eust fallu descendre d'un ton entier comme S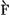 Ś, LSL, RVRGa naar voetnoot6bis), car la voix affecte naturellement a ne s'eloigner pas tant d'un ton ou elle doit revenir incontinent, de sorte que l'on diminue ces tons: mais d'en avoir fait justement des demitons majeurs, il y a deux raisons pour cela, l'une que ces sons de F*, S*, V*Ga naar voetnoot7) sont de ceux qui sont consonance Ś, LSL, RVRGa naar voetnoot6bis), car la voix affecte naturellement a ne s'eloigner pas tant d'un ton ou elle doit revenir incontinent, de sorte que l'on diminue ces tons: mais d'en avoir fait justement des demitons majeurs, il y a deux raisons pour cela, l'une que ces sons de F*, S*, V*Ga naar voetnoot7) sont de ceux qui sont consonance
| ||||||||
[pagina 32]
| ||||||||
avec plusieurs des sons naturels de l'octave, comme F* contre R, L et C. S* contre M et C. ce qui addoucit et accommode le chant suivi aussi bien que la symphonie comme il a estè dit cydevant. L'autre raison est que l'on estoit desia accoustumè aux intervalles des demitons majeurs en chantant FMF, et VCV. Dans la suite on a encore adjoutè le M♭ non pas tant pour avoir le semiton majeur au dessus du R que pour avoir la tierce mineure dessus le V et la majeure dessous le S ce qui donne en mesme temps la 6 majeure contre V2 et la sixte mineure contre S vers en bas. L'on adjoute encore d'autres tons quelquefois et avec beaucoup de raison dont nous parlerons cy apresGa naar voetnoot8).
§ 3. Puisque les intervalles du chant ont leur origine des consonances, il est necessaire . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Consultez les p. 362-364 du T. XIX (Huygens y parle e.a. de l'histoire des marteaux de Pythagore; voyez là-dessus l'Avertissement qui précède) jusqu'à l'alinéa se terminant par: et la proportion dans les autres nombres est de 5 à 2. Dans ces pages il est question des ‘répliques’ auxquelles Huygens fait allusion à la fin du § précédent: voyez l'alinéa suivant.
Ainsi parce que les chordes de 3 a 2 font la 5te, ce sera aussi une consonance que de 6 a 2 ou de 3 a 1, que l'on appelle la 12e, et c'est une replique de la 5te. Et la raison pourquoy cela arrive est la mesme qui fait la douceur des autres consonances dont nous allons parler. Il est constant par l'experience, et ceux qui ont tant soit peu d'oreille pour la musique ne peuvent nier, que les consonances suivant les proportions susdites ne soient tres parfaites et meilleures que quand on s'ecarte de ces veritables proportions numeriques. Et ceux qui ont osè soustenir le contraire et que la 5 ne consistast pas dans la raison de 3 a 2 ou n'avoient pas l'oreille capable d'en juger ou croioient avoir une raison pour cela, mais ils concluoi[en]t mal. En marge: StevinGa naar voetnoot9). dont nous parlerons cy apresGa naar voetnoot10). | ||||||||
[pagina 33]
| ||||||||
§ 4. Quand on examine les tremblements des chordes ce que je pense que Galilee a fait le premier . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Consultez les p. 364-365 du T. XIX jusqu'à la fin de la Pièce de ce Tome, c.à.d. jusqu'aux mots: lesquelles on tendra toutes perpendiculaires avec un poids au bout. | ||||||||
[pagina 34]
| ||||||||
§ 5. Quelles consonances sont estimees plus agreables que d'autres. Et s'il n'y a pas encore d'autres consonances outre celles qui sont maintenant reputees dans ce nombre. On trouve que des consonances les unes sont plus agreables que les autres, et que ce sont celles qui plaisent le plus dont les battements se rencontrent le plus frequemment ensemble, exceptè pourtant l'unisson dont tous les battements se rencontrent et qui | ||||||||
[pagina 35]
| ||||||||
pour cela ne fait autre effect qu'un son tout seul; et encore l'octave et ses repliques parce qu'elle ressemble a l'unissonGa naar voetnoot11). Hors mis celles là la 12 ou la 5 par dessus l'octave est trouuee la plus agreable, dont la proportion est de 3 a 1, de sorte qu'a chaque battement de l'air du son grave, l'aigu en fait 3. au lieu que dans la 5e les trois battemens du ton aigu ne se rencontre[nt] que avec les 2 battemens du ton grave, et c'est ce qui fait que la 12 est plus agreable que la 5. Apres la 12e la prochaine en douceur est la 17e ou la tierce majeure par des- | ||||||||
[pagina 36]
| ||||||||
sus deux octaves dont la raison est de 5 a 1, et partant les 5 battements du ton aigu se font contre chaque battement du ton grave. Dans la 10e qui est la 3e majeure par dessus une octave les 5 battemens du ton aigu ne se rencontrent qu'avec les 2 du ton grave, et dans la 3e majeure elle mesme, les mesmes 5 battements se font contre 4 du ton grave, ce qui la rend moins belle que la 10e, et celle cy moins belle que la 17 ou seconde replique de la tierceGa naar voetnoot12). Quand on compare selon cette maxime la 4te avec la 3e majeure on diroit que celle cy devroit estre moins agreable que la 4te, car a tous les 3 battemens se rencontrent les 4 dans la quarte; et dans la tierce a tous les 4 battements se rencontrent les 5. Et cependant la 4te semble la moins bonne des deux. L'on voit la mesme chose generalement par tout, que de deux consonances celle dont la replique premiere ou seconde devient en raison multiple paroit meilleure que l'autre. Et il semble que la raison soit qu'en entendant quelque ton on suppose et semble entendre en quelque façon son octave plus haute ou mesme la double octave. Et on l'entend effectivement en sonnant quelque chorde, ou grande cloche, et mesme la 12e et la 17eGa naar voetnoot13). De sorte que comme les repliques de ces consonançes sont en raison multiple dont les rencontres de battements sont plus frequentes que des autres, on estime la consonance mesme par la beautè de ces repliques. Ainsi donc puisque les repliques de la tierce sont la 10e et la 17, dont l'une aux 2 battemens du son grave et l'autre a chacun en a 5 du son aigu, et qui pour cela sont meilleures que la 4e en qui la rencontre ne se fait qu'a tous les 3 coups du son grave et de mesme a toutes ses repliques; on trouve la 3 majeure elle mesme meilleure que la 4teGa naar voetnoot14). On peut examiner la preference des autres consonances suivant ces mesmes regles et il est utile de connoistre ces degrez de bontè, quoy qu'il soit vray que tous les gouts ne s'accordent pas tout a fait en ce jugement. Ce qui paroit bien manifestement de ce | ||||||||
[pagina 37]
| ||||||||
que les anciens ne trouvoient pas seulement que les 3ces ni les 6tes fussent des consonancesGa naar voetnoot15), et qu'ils reconnoissoient la 4te parmy les premieres. Il est bon a ce propos d'examiner s'il n'y a pas d'autres consonances que celles que nous avons definies cy dessus et s'il y a quelque raison de l'assurer. Car peut estre nous pourrions faire la mesme faute que les anciens. Les proportions des nombres qui constituent les consonances sont reputees celles d'un des nombres 1, 2, 3, 4, 5, 6, à quelqu'autre de ce mesme rang, y comprenant aussi les doubles et les moitiez de ces nombres ou mesme leur autres multiples et soumultiples par 2, ce qui ne fait qu'adjouter la consonance a une ou a plusieurs octaves ou bien l'en oster. Le nombre de 7 ni autre nombre primitif ou composè de premiersGa naar voetnoot16) n'y sont point admis. Et il y en aGa naar voetnoot17) qui attribuent cela à la perfection du nombre 6, lequel ils appellent harmonique pour cette raison. Cependant a bien examiner la chose et sans prejugè l'on trouvera que le nombre de 7, comparè a d'autres, n'est pas incapable de produire une consonanceGa naar voetnoot18), mais que celles qu'il produit ne sont pas compatibles avec les consonances desia establies, ni mesme si bonnesGa naar voetnoot19). |
|