Oeuvres complètes. Tome XX. Musique et mathématique
(1940)–Christiaan Huygens–
[pagina 151]
| |
C. Commentaire sur une tableGa naar voetnoot1).La 2de colomne de cette tableGa naar voetnoot2) contient les nombres qui expriment les longueurs des 31 chordes qui font les 31 intervalles egaux suivant la nouvelle division, la chorde entiere estant supposee de 100000 parties et par consequent sa moitiè, qui fait l'octave contre elle de 50000. Et a costè sont les noms des tons, qui sont emploiez d'ordinaire et des * pour quelques chordes enarmoniques, dont celle auprès du sol ♯ est la plus necessaire. Ces nombres ont estè trouvez par ceux de la 1re colomne qui sont leur logarithmes respectifs. Et pour avoir ceux cy, j'ai divisè le logarithme de 2 qui est 0,30102999566 par 31, d'ou est venu le nombre N 97106450, que j'ay adjoutè continuellement au logarithme de 50000, qui est 4,6989700049. D'ou sont procedèz tous ces logarithmes jusqu'au plus grand 4,9999999993, qui manquant si peu de 5,0000000000, fait voir que le calcul a este bien fait. Ceux qui entendent les Logarithmes scavent qu'il a falu faire ainsi pour avoir les 30 nombres proportionaux entre 100000 et 50000. La 3e colomne comprend les longueurs des chordes suivant le Temperament ordinaireGa naar voetnoot3), et dans la 4e colomne sont leurs logarithmes; qui ont estè trouvez par les nombres Algebriques de la 5e et 6me colomne. Et ceux cy par la methode qui s'ensuitGa naar voetnoot4), et qui fait voir comment ce Temperament pourroit avoir estè trouvè lors qu'il estoit encore inconnu. J'ay nommè a la longueur de toute la chorde dont le ton soit Vt d'où la moitiè estoit ½a, dont le ton est marquè Vt2. Pour la longueur de la chorde sol j'ay mis x, m'imaginant que ce fut la quinte au dessus de ut. Et, faisant l'intervalle de sol Re2 | |
[pagina 152]
| |
derechef d'une quinte il faloit que comme a à x ainsi fut x à xx/a longueur de la chorde Re2. Et de cellecy l'octave en bas, scavoir Re devoit estre 2xx/a; et d'icy montant derechef d'une quinte en La, sa longueur devoit estre 2x3/aa, parce que comme a à x ainsi 2xx/a a 2x3/aa. Et montant encore d'une quinte en Mi2, elle estoit 2x4/a3 et son octave en bas Mi, 4x4/a3. Or je scavois que l'intervalle de Ut, La devoit faire la sexte majeure, et qu'on l'emploioit pour tel. Mais en posant les quintes justes selon la proportion de la 3 à 2, c'est a dire en faisant x ∞ ⅔ a, on avoit 2x3/aa ∞ 16/27 a. Donc la proportion de a à 16/27 a devoit estre comme de 5 a 3 qui est celle de la sexte majeure, ce qui n'est point, car la raison de a à 16/27 a, ou bien la raison de 27 a 16, excede celle de 5 à 3 de la raison de 81 à 80, qu'on appelle le Comma, donc en voulant que les quintes soient justes, la sexte majeure surpassoit la vraye d'un comma entier, ce que l'oreille ne peut pas souffrir estant pres de 1/9 de ton. Mais outre cela l'intervalle de Ut, Mi, qu'on veut que ce soit une tierce majeure, devient plus grand que le veritable, car Mi a estè trouvè 4x4/a3 qui devient 64/81 a si on suppose x ∞ 2/3 a. Or la raison de a a 64/ 81 a, ou de 81 a 64, est plus grande que celle de 5 à 4 (qui donne la tierce majeure juste), de la raison de 81 à 80, qui est encore justement celle du Comma. Et les tierces mineures seront moindres que les veritables de ce mesme Comma parce qu'elles sont le complement a la quinte des tierces majeures. J'ay donc vu qu'il estoit bon de diminuer les quintes de quelque chose en posant x plus grand que 2/3 a, parce que de là les sextes majeures decroissoient estant trop grandes; et qu'en mesme temps la tierce majeure Ut Mi se diminuoit aussi parce que 4x4/a3 devient plus grand lors qu'on augmente la quantitè de x. Mais de combien plus grande faloit il prendre x que 2/3 a. La voie du milieu parut estre la meilleure qui estoit de faire que les quintes et les sextes majeures differassent egalement des vraies, les unes en perdant les autres en excedant. J'ay donc fait que la longueur de x fut à 2/3 a comme 3/5 a à 2x3/aa, c'est a dire comme la longueur de La parfaite à celle qui a estè trouvée cy dessus. d'ou vient l'equation 2x4/aa ∞ 6/15 aa et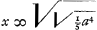 . .
| |
[pagina 153]
| |
Par là la chorde Mi qui a estè trouvée 4x4/a3 devient 4/5 a, x estant donc supposée telle les quintes seront diminuees de la mesme quantitè que les sextes majeuresGa naar voetnoot5). Or la raison de 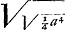 a ⅔a est la mesme que celle qui constitue le quart du comma, puisque cette raison estant quadruplée fait la raison de 81 à 80 ou du comma entier, comme il est aisè de voir en prenant le quarre quarrè de chacun des deux termes. a ⅔a est la mesme que celle qui constitue le quart du comma, puisque cette raison estant quadruplée fait la raison de 81 à 80 ou du comma entier, comme il est aisè de voir en prenant le quarre quarrè de chacun des deux termes.
Diminuant donc la quinte Ut, sol, et par consequent aussi les autres de ¼ de Comma, les sextes majeures surpasseront d'autant les veritables; et pour les quartes et les tierces mineures qui sont les complements a l'octave de ces consonances, les premieres surpasseront les vraies du mesme ¼ de comma et les autres defaudront d'autant. |
|

