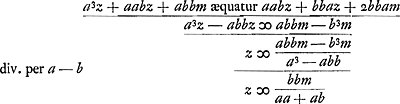Oeuvres complètes. Tome XX. Musique et mathématique
(1940)–Christiaan Huygens–
[pagina 303]
| |
Appendice IGa naar voetnoot1)
| |
[pagina 304]
| |
Haec quantitas sive multiplicetur in a3 + aab et addatur abbm + b3m sive multiplicetur in aab + bba et addatur 2bbam, efficit eandem in utroque casu quantitatem, nempe 2abbm + b3m. Hinc itaque secundum authorem terminatio quaesita porro inveniri poterit adeoque ipsa Circuli quadratura. Dicet enim eandem hanc quantitatem eodem modo componi ex quibuslibet seriei terminis convergentibus quo componitur ex terminis a3 + aab et abb + b3. ac proinde etiam ex ultimis, qui aequales sunt. Sit ultimus terminus x, qui itaque multiplicatus in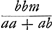 , alterque qui itidem est x, in m, facient , alterque qui itidem est x, in m, facient 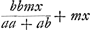 quae aequari debent 2abbm + b3m. Unde quae aequari debent 2abbm + b3m. Unde 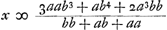 .
Haecitaque Terminatio seriei convergentis x, quae repraesentat circuli sectorem, cum inventa sit, dabitur Circuli quadratura. At non est vera haec terminatio. Nam posita b ∞ 2a, fiet, in primis terminis, a3 + aab aequalis quartae parti abb + b3. Hoc est .
Haecitaque Terminatio seriei convergentis x, quae repraesentat circuli sectorem, cum inventa sit, dabitur Circuli quadratura. At non est vera haec terminatio. Nam posita b ∞ 2a, fiet, in primis terminis, a3 + aab aequalis quartae parti abb + b3. Hoc est
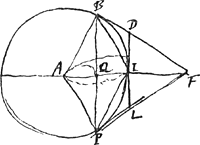 [Fig. 28].
triangulum BAP [Fig. 28] aequale ¼ trapezij ABFP. Ideoque arcus BI sextans circumferentiae. Porro trapez. ABIP erit aab + bba duplum trianguli ABP, et polygonum ABDLP, 2bba ∞ 8/3 trianguli ABP, deinde z erit 4/3 m. Et Terminatio x sive 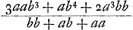 ,
hoc est sector ABIP ad triangulum ABP sive a3 + aab, ut 16 ad 7, quod est falsum. Nam dividendo esset segmentum BPI ad triangulum ABP, sive ad triangulum BIP ut 9 ad 7 quae ratio minor est quam 4 ad 3. ,
hoc est sector ABIP ad triangulum ABP sive a3 + aab, ut 16 ad 7, quod est falsum. Nam dividendo esset segmentum BPI ad triangulum ABP, sive ad triangulum BIP ut 9 ad 7 quae ratio minor est quam 4 ad 3.
Quid vero deceperit authorem hinc intelligetur. In serie convergente cujus primi termini a, b secundi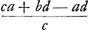 , , 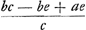 cujus terminatio investiganda proponitur prop. 7. in hac igitur quaerendo quantitatem z illa invenitur aequalis me/d, nam quod ille dicit
cujus terminatio investiganda proponitur prop. 7. in hac igitur quaerendo quantitatem z illa invenitur aequalis me/d, nam quod ille dicit 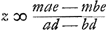 , non advertit divisionem fieri posse per a - b, et hinc forsan erroris occasio extitit. Cum autem sumtis a, b, pro quibuscunque seriei terminis, sequentes sint , non advertit divisionem fieri posse per a - b, et hinc forsan erroris occasio extitit. Cum autem sumtis a, b, pro quibuscunque seriei terminis, sequentes sint 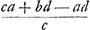 , , 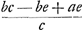 ex hypothesi; manifestum est, ad quoscunque terminos sese proximè sequentes investigetur z, illam eandem quantitatem semper habituram, cum semper sit z ∞ me/d, quae ex hypothesi; manifestum est, ad quoscunque terminos sese proximè sequentes investigetur z, illam eandem quantitatem semper habituram, cum semper sit z ∞ me/d, quae
| |
[pagina 305]
| |
m, e, et d, sunt quantitates datae. Proinde cum z sive me/d, multiplicata in a, additaque ad hoc productum b multiplicata in m, producat quantitatem 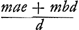 (quam author dicit esse (quam author dicit esse 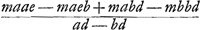 , non videns divisionem fieri posse per a - b) eademque quantitas eodem modo producatur ex terminis seriei secundis, ut sequitur ex inventione quantitatis z; atque eodem quoque modo ex tertijs quo ex secundis, quoniam z ∞ me/d eadem semper quantitas ad primos et secundos, et ad secundos et tertios terminos invenitur, apparet etiam ex primis et ex tertijs terminis eodem modo eandem quantitatem , non videns divisionem fieri posse per a - b) eademque quantitas eodem modo producatur ex terminis seriei secundis, ut sequitur ex inventione quantitatis z; atque eodem quoque modo ex tertijs quo ex secundis, quoniam z ∞ me/d eadem semper quantitas ad primos et secundos, et ad secundos et tertios terminos invenitur, apparet etiam ex primis et ex tertijs terminis eodem modo eandem quantitatem 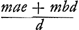 componi. Atque hinc facile perspicitur componi. Atque hinc facile perspicitur
 [Fig. 29]
eandem ex quibuslibet alijs seriei ejusdem terminis eodem semper modo compositum iri, et denique etiam ex ultimis. qui cum aequales sint, si alter ponatur ∞ x, etiam reliquus erit x, unde 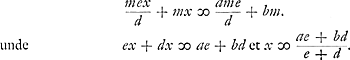 nam author rursus hic non vidit divisionem fieri per a - b. Est autem haec series nihil aliud quam quae his lineis [Fig. 29] repraesentantur, ubi FG est b; LG a; LF b - a. Tum ut c ad d, hoc est, ut 7 ad 2, ita fit FL ad LP, quae addita ad LG facit minorem secundorum terminorum PG. Et rursus ut c ad e, hoc est ut 7 ad 3, ita fit LF ad FN, quae ablata ab FG, facit majorem secundorum terminorum NG. Et continuando porro ponitur PS 2/7 NP, et NQ 3/7 NP, et ita porro in infinitum. Unde tandem terminationis ultimum quoddam punctum concipitur, et recta quae ab eo puncto ad G extenditur est hic terminatio quae quaeritur quam author recte dicit esse 33⅗. Haec autem facile quoque aliunde determinari potest. Nam cum partes hinc et inde in linea FL acceptae, ut LP, FN, et reliquae porro sint semper ut 2 ad 3, apparet et punctum terminationis quaesitae ita dividere debere totam FL ut pars versus L sit ad reliquam ut 2 ad 3, tota autem FL est partium 14 qualium LG, 28. Ergo ab L ad punctum terminationis sunt ⅖ ex 14, hoc est 5⅗, quae additae ad LG 28 faciunt 33⅗. Porro author cum hanc determinationem recte inveniri methodo sua animadvertisset, existimavit cujuscunque alterius seriei convergentis terminationem inveniri similiter posse, si inventa esset quantitas quae eodem modo componeretur ex primis terminis seriei convergentis et ex secundis. Quo dato, (non autem concesso, ob rationes postea adducen- | |
[pagina 306]
| |
das) non sequitur inde, ut vult author, si quantitas ejusmodi nulla esse possit, tunc neque terminationem seriei analyticam fore respectu terminorum seriei. Nam etsi verum esset, tali quantitate data quae eodem modo componitur ex primis atque ex secundis seriei terminis, tunc ejus ope inventum iri terminationem seriei, et illam terminationem esse repertam, eodem quoque modo compositam fore ex primis, secundis, aut alijs quibuslibet seriei terminis. non inde sequetur terminationem seriei, aliâ forsan methodo repertam, etiam debere componi eodem modo ex primis atque ex secundis seriei terminis. Itaque male rationem colligit author. Dico autem porro, non esse verum, data quantitate quae eodem modo ex primis et ex secundis seriei terminis componitur, inveniri inde semper posse seriei terminationem. quod jam patuit ante, cum quantitas 2abbm + b3m, eodem modo componatur ex terminis seriei primis a3 + aab et abb + b3, quo ex secundis aab + bba, et 2bba, nec tamen per eam vera terminatio seriei inveniatur. Quare autem non rectè succedat terminationis inventio in hac serie, cum secus eveniat in serie quam ponit author prop. 7, et in alijs quibusdam, ratio differentiae haec est, quod in serie prop. 7 cum invenitur quantitas z ∞ me/d, in illa non occurrat quantitas a nec b, unde fit ut sive ad primos et secundos terminos inveniatur z, five ad secundos et tertios, semper eadem quantitas inveniatur. Quod cum ita contingit, sequitur ope ipsius z inveniri quantitatem quae eodem atque unico modo ex primis, secundis, tertijs alijsque quibuslibet seriei terminis componatur, ut folio praecedenti ostensum fit. Sed cum quantitates a et b, vel alte rutra habentur in quantitate z, tunc z non erit eadem quantitas ad primos et secundos, ac ad secundos et tertios terminos teperta. Et invenietur quidem, per primam z, quantitas quae eodem modo ex primis et ex secundis seriei terminis componitur, et per alteram z, invenietur quantitas eodem modo composita ex secundis et ex tertijs terminis. Sed quantitas haec posterior non erit eadem cum priori, ac proinde cum non sit inventa quantitas quae eodem modo ex quibuslibet duobus seriei terminis componitur, nec poterit inveniri per eam seriei terminatio. Quod si vero quantitas aliqua inveniri possit eodem modo composita ex primis et ex secundis seriei terminis, absque inventione quantitatis z, tunc illa quantitas sufficit ad inventionem terminationis. ut si detur series convergens cujus primi termini a, b, secundi √ ¢ aab, √ ¢ bba, semperque sequentes duo ex duobus praecedentibus eodem hoc modo componantur, hic habebitur quantitas ab, eodem modo ex primis et ex secundis terminis composita, nempe ex multiplicatione terminorum simplici. Constatque eandem eodem modo etiam ex tertijs et alijs quibuslibet seriei terminis componi, quoniam a et b indifferenter pro quibuslibet seriei terminis sumi possunt. Itaque et ex ultimis qui aequales sunt. qui si vocentur x singuli erit xx ∞ ab et x ∞ √ ab terminatio quaesita. Exemplum autem ab authore allatum propositione ... absurdum est, nam si primi | |
[pagina 307]
| |
termini sint a et b, secundi √ ab et aa/√ ab fient rursus tertij termini a et b. Adeo ut haec non sit series convergens, cujus proinde neque terminatio ulla esse potest, etsi author eam invenisse existimet.
Aliud initiumGa naar voetnoot1). Primo male ratiocinatur prop. 11. cum ita colligit. Si terminatio proposita seriei esset analytica cum terminis seriei, oporteret eam terminationem eodem modo componi ex primis et ex secundis terminis. Male inquam sic colligit. Nam licet verum sit terminationem, si inventa sit methodo authoris, eodem modo compositam fore ex primis et ex secundis, alijsve quibuslibet seriei terminis, non sequitur, si alio sorsan modo terminatio seriei inventa sit, etiam tunc eodem modo ex primis et ex secundis terminis compositam fore. Oporteret enim, ut hoc sequeretur, ostendisse antea authorem nulla alia quam sua methodo terminationem seriei posse inveniri. Vel saltem quotiescunque aliqua methodo terminatio reperiri potest etiam sua methodo eam reperiri posse. Rursus hallucinatur cum paulo post ait, At nulla quantitas potest eodem modo componi ex terminis a3 + aab et abb + b3, quo componitur ex terminis aab + bba, et 2bba. |
|