Oeuvres complètes. Tome XX. Musique et mathématique

[p. 474]

IX¹⁾.
Cycloïde et cissoïde; solides de révolution et centres de gravité.
[1691 ou 1692]

En marge: Haec pendent e Theoremate pag. 14 posteriore²⁾.

ABCD Semicyclois [Fig. 98]³⁾. FH tangens. FK parall. DC. HK parall. DA. K est punctum in curva CKQ. Erit spatium CFK ∞ CFG⁴⁾.

[Fig. 98]

Sit DRS Cissoides, ad asympt. AT. applicata NO, (posita KFENO linea recta) erit aequalis ML sive GH, hoc est FK. unde spat. DNO ∞ CFK seu CFG. idque

1) Manuscrit H, p. 9 r (p. 17 suivant la numération de Huygens). Les p. 8 et 55 (Huygens) portent respectivement les dates 19 Dec. 1691 et 17 Apr. 1692.

2) Il s'agit ici de la Pièce de ‘décembre 1691’ (voyez cependant sur cette date la note précédente) que nous avons publiée comme Appendice à une lettre de Huygens au Marquis de l'Hospital à la p. 309 du T. X. Consultez sur les notations ϰ, λ etc. de cette Pièce la suite du présent Tome (p. 511 etc.).

3) La présente Pièce se rattache aussi plus ou moins à celle de septembre 1691, tirée de la f. 126 r du Manuscrit G (on trouve les dates 1 Sept. 1691 et 1 Oct. 1691 respectivement sur les p. 123 r et 127 v) que nous avons publiée, comme Appendice à des pièces antérieures, aux p. 377-378 du T. XIV. Nous n'aurions guère pu y joindre la présente Pièce: les recherches de Huygens de 1658 et 1659 constituant ces ‘piêces antérieures’ se rapportaient exclusivement aux ‘propriétés géométriques de la cycloïde’ (voyez la p. 347 du T. XIV).

4) Comparez la figure et le texte de la p. 309 du T. X, déjà citée dans la note 2.

[p. 475]

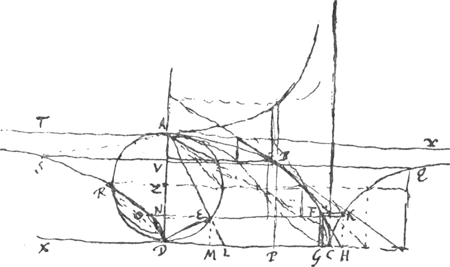
ubique. Nempe et spat. SVD ∞ BCP. Et totum spatium Cissoidis infinitum ∞ Cycloidi dimidiae ACD.

Item solidum ex spatio infinito Cissoidis circa axem DX aequale solido ex spatio Cycloidis ACD circa axem DC.

Sed spatij Cycloidis ACD centrum gravitatis distat ab DC 5/12 AD⁵⁾. Ergo spatij infiniti DSTA centrum gravitatis distat 10/12 seu ⅚ AD ab DC. seu ⅙ AD ab AT. quod et aliunde apparet quia AN in NO ∞ DN in NE. ideoque semicirculus DEA circa DM vel AT revolutus facit solidum aequale solido Cissoidis infinito circa AT. unde radius DZ in semicirculum AED ductus aequale solidum facit ac spatium infinitum DSTA in distantiam centri gravitatis suae ab AT. Est autem spatium istud triplum semicirculi. Ergo dicta distantia centri gravitatis erit ⅓ radij ZD.

5) Dans sa lettre du 1 janvier 1692 à Leibniz Huygens lui rappelle (T. X, p. 224) les ‘profondes speculations de Mr. Pascal’ et de ‘Wallis’ sur ‘le centre de gravitè de la demie Cycloide’.