Oeuvres complètes. Tome XXI. Cosmologie

[p. 316]

II.
De l'équation du temps.¹⁾
[1680]

Le temps de chaque jour naturel ou apparent, scavoir d'un midy a l'autre, est celuy d'une revolution entiere de l'equateur, par le meridien et de plus d'une partie de l'equateur qui passe le meridien en mesme temps que l'arc de l'ecliptique que le soleil a parcouru entre les deux midis.

Or cette partie de l'ecliptique estant tantost plus grande tantost plus petite a cause du mouvement inegal du soleil, et ayant des inclinaisons differentes a l'egard de l'equateur a cause de l'obliquitè de l'ecliptique; il en arrive que cette partie de l'equateur qui passe le meridien ensemble avec la dite partie de l'ecliptique, est aussi de differente grandeur en different temps; et partant les jours naturels necessairement inegaux.

L'on a besoin dans les calculs d'astronomie de comparer ces jours inegaux avec des jours egaux de moyene longueur, qui sont chacun d'une revolution entiere de l'equateur, et d'un arc du mesme de 59′8″. scavoir egal au moyen mouvement journalier du soleil dans l'ecliptique. Et pour se figurer ces jours egaux, il faut s'imaginer un soleil qui partant du principe d'Aries en mesme instant que le vray soleil fasse son tour annuel dans l'equateur, et cela d'un mouvement tousjours egal, qui seroit journellement de 59′.8″.

Une horloge tres juste estant une fois accordee à la mesure et a l'heure de ces jours moyens, marqueroit en suite tousjours midy, quand ce soleil imaginè retourneroit au meridien, le veritable soleil ayant alors bien souvent desia passè le meridien, ou n'y estant pas encore arrivè. Et la difference peut aller en ce siecle ou nous sommes jusqu'a une demie heure et un peu d'avantage. Ce qui dans le calcul du mouvement de la lune sur tout est fort considerable, parce qu'en une demie heure elle fait un arc d'environ 15 minutes. Et il ne faut pas esperer de pouvoir jamais trouver la veritable theorie de cette planete si on n'emploie au calcul de son mouvement la veritable equation du temps. En quoy presque tous les astronomes et mesme les plus habiles ont failly qui se fatiguoient en vain à forger des epicycles les uns sur les autres, pour representer l'irregularitè du cours lunaire; Tycho Brahe ayant osè introduire une equation de

1) La Pièce est empruntée aux p. 27-30 du Manuscrit F. La p. 39 porte la date du 16 novembre 1680.

[p. 317]

temps particuliere pour la lune, differente de celle qu'il establissoit pour les autres planetes, ce qui est tres absurde.

Pour bien comprendre donc en quoy consiste l'equation du temps, concevons une horloge ajustée, comme il a estè dit, à la moyene mesure des jours. ce que j'ay montrè comme il se fait par le moyen des estoiles fixes.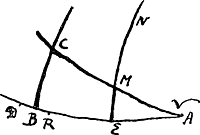

[Fig. 89]

Soit maintenant [Fig. 89] AB l'equateur, AC l'ecliptique, A leur intersection ou le principe d'Aries. ME un meridien fixe sous lequel passent les degrez des dits cercles par le mouvement journalier, du costè B vers A. Soit donnè un espace de temps apparent, par exemple depuis le midy du 10 avril 1680 jusqu'au midy du 12^e Juin de la mesme année; et que l'on veuille scavoir combien il s'est ecoulè de temps egal dans cet espace. Ou bien en prenant pour Epoque ou commencement commun du temps apparent et de l'egal le midy du 10 Avril, qu'il faille reduire le moment du midy apparent du 12 Juin au temps egal. Il s'agit en tout cela de scavoir, lors qu'on aura accordè l'horloge susdit avec le soleil, au midy du 10 avril, quelle heure il marquera lors que le soleil sera au midy le 12^e Juin.

Soit M le lieu du soleil dans l'ecliptique au midy du 10 avril. C le lieu du soleil au midy du 12^e juin, et l'ascension droite de C soit B. Et parce que l'horloge commence du mesme midy du 10 avril, concevons que le soleil imaginaire de l'Equateur commence alors d'aller depuis E, ascension droite du soleii en M. Il faudroit maintenant scavoir la quantitè de l'arc ED, que je suppose que le soleil imaginaire a fait dans l'intervalle donnè, c'est a dire dans le temps que le vraij soleil cst venu de M en C, car alors je diray que C estant parvenu (par le mouvement qu'on appelle du premier mobile) au meridien fixe NME, et en mesme temps le point B; le point D ou soleil imaginaire, en cas que l'arc ED soit plus grand que EB, aura encore besoin du temps qu'il faut pour passer l'arc BD, pour venir au meridien. Prenez qu'il faille 5 minutes, donc au midy apparent du 12^e Juin, il sera encore 5 minutes devant midy a l'horloge. Et ainsi l'on voit que, quand BE, difference des ascensions droites des lieux du soleil aux deux termes du temps apparent donnè, est plus petit que l'arc ED, qui est le mouvement egal qui convient a l'intervalle du mesme temps apparent; il faut oster du temps apparent autant qu'il en convient a l'exces de l'arc DE sur BE, pour avoir le point du temps egal, ou l'heure de l'horloge. Et au contraire si l'arc ED eust estè plus petit que BE. Tout cecy est fort connu des astronomes, et c'est la dessus qu'est fondée la regle des Anciens²⁾, qui est: Pour reduire le temps apparent au temps egal, ayez

2) On trouve cette règle, énoncée un peu plus sommairement, vers la fin du troisième livre de l'Almageste de Ptolémée. Et aussi dans l'alinéa ou ‘sectio’ du livre 3 de la première partie du Nouvel Almageste de Riccioli que Huygens cite un peu plus loin.

[p. 318]

pour les deux extremitez du temps apparent donnè le lieu moyen et le veritable du soleil, et l'ascension droite du veritable lieu. Puis prenez la difference des lieux moyens, ostant tousjours le premier en date du dernier; et adjoutant 360 degrez quand le dernier est de moins de degrez que le premier. Prenez de mesme la difference des ascensions droites, et conferez entre elles ces 2 differences. qui si elles sont egales, il n'y a point d'equation a faire, mais 1. si la difference des ascensions droites est plus grande que la difference des lieux moyens, alors il faut adjouter l'exces converti en temps, au temps apparent, pour avoir le temps egal. 2. Mais si la difference des ascensions droites est plus petite que la difference des lieux moyens, il faut soustraire ce qui defaut converti en temps, du temps apparent pour avoir le temps egal. Que s'il faut reduire le temps egal au temps apparent (comme le temps d'une Eclipse calculée par les tables, au temps apparent qu'elle sera observee) 3. la regle alors est, que la difference des ascensions droites estant plus grande que la difference des lieux moyens, l'on doit soustraire l'exces, converti en temps, du temps moyen, pour avoir le temps apparent, car alors R arrivera au meridien NME quand B ne sera pas encore en ce meridien, et partant l'heure de l'horloge plus avancée que celle du veritable soleil. 4. Mais si la difference des ascensions droites est plus petite que la difference des lieux moyens; il faut adjouter l'exces, converti en temps, au temps egal, pour avoir le temps apparent. Ce sont la les veritables regles, et il faut bien prendre garde quand on en a besoin de ne pas s'y abuser, en adjoutant ce qu'il faut soustraire, ou au contraire.

De constituendis Epochis Tabularum duae sunt auctorum sententiae. Alij enim ad Tempus apparens eas referunt ut Alphonsini, Ptolemaeus, Copernicus. Alij ad Tempus aequale sive medium ut vocant, in quibus Tycho, Longomontanus, Lansbergius, Keplerus, Bullialdus³⁾ &c. Itemque Ricciolus, ut patet ex ijs quae scribit Almag. parte 1. lib. 3. cap. 33. sect. 3⁴⁾. In exemple suo errat in computando temporis intervallo ab observatione ad finem anni. Sed recte intelligit pag. 256 ejusdem partis⁵⁾ ubi Epocham Lunaris Longitudinis constituit. Ipsa vero methodus ipsius omniumque qui ad tempus medium Epochas accommodant prorsus erronea est. Copernicus autem recte suam Lunae Epocham constituit, credo Ptolemaeum secutus. Et haec sola vera est ratio.

3) Voyez sur Tycho Brahé, Kepler et Boulliau les p. 523-524 du T. XV. Consultez aussi la note 18 de la p. 33 qui précède.

4) Comparez sur ce passage la note 2 qui précède. Riccioli y cite les noms de tous les astronomes qu'on vient de lire dans le texte.

5) Lib. 4. cap. 24. ‘De Constituendis Epochis Lunarium Motuum’.