Oeuvres complètes. Tome XXII. Supplément à la correspondance. Varia. Biographie. Catalogue de vente

[p. 577]

Années 1661-1666.

[p. 579]

§ 1. À la Haye mai 1661-mars 1663.

Deux jours après son arrivée en Angleterre Huygens s'était rendu chez Alexandre Bruce - qui en 1663 devint comte de Kincardine - pour qui il avait une commission¹⁾. Il le connaissait avant ce temps, au moins depuis 1658, puisqu'on trouve son nom - comme toujours, lorsque Huygens parle de lui²⁾, sous la forme ‘Brus’ - dans la liste des personnes qui reçurent l' ‘Horologium’³⁾. Ceci fait voir en même temps qu'alors déjà Bruce s'intéressait aux horloges. Il avait quitté l'Écosse en 1657 et s'était fixé pour quelque temps à la Haye après avoir visité l'Allemagne. Le nom Bruce ne se trouve pas avant ce temps dans la Correspondance du père Constantyn; suivant une note du T. IV⁴⁾ A. Bruce ne vint à la Haye qu'en 1659; s'il en est ainsi, ce qui nous semble improbable, nous nous demandons comment Huygens a pu le connaître des 1658⁵⁾. Après juin 1659 Huygens le connut sans doute encore mieux, puisqu'en ce mois il épousa une sille du diplomate Cornelis van Aerssen, fils de François⁶⁾. À Londres Huygens vit Bruce assez souvent. Nous observons en passant qu'il y visita aussi l'atelier des horlogers Fromanteel⁷⁾. C'est de Bruce qu'il est question dans la lettre de Huygens à Moray du 24 juin 1661⁸⁾. Nous apprenons par cette lettre que Bruce avait commandé à la Haye pour Moray une horloge à pendule de trois pieds. Il semble possible que déjà pendant le premier séjour de Bruce à la Haye Huygens et lui aient parfois observé conjointement la marche de certaines horloges, alors que l'horloge à pendule était une nouveauté, et qu'ils aient discouru sur les moyens d'en améliorer la marche, surtout pour le problème des longitudes, donc pour le transport des horloges sur mer, car nous ne voyons pas que Bruce se soit intéressé à l'astronomie. Ce qui est certain c'est qu'ils travaillèrent ensemble pendant un deuxième

1) Voyez le 14 mars 1661, à Paris.

2) Même dans la lettre officielle à J. de Witt, p. 80 qui précède. Ceci porte à croire qu'à la Haye Bruce était généralement appelé Brus.

3) P. 209 du T. II.

4) P. 256.

5) Comparez notre note 10 à la p. 161 du T. XVII.

6) Voyez sur eux la p. 103 du T. IV.

7) T. XVII, p. 189.

8) Et non pas de Robert Bruce, comme le dit la note à la p. 384 du T. III, citée dans le texte. Même erreur dans la note 10 de la p. 519 du T. VII; mais là elle a été corrigée dans les ‘Additions etc.’.

[p. 580]

ou du moins pendant un troisième séjour de Bruce à la Haye en 1662. Voyez sur le mois de février 1662 la p. 160 du T. XVII. Le 9 novembre de cette année Huygens écrit que ‘M. Brus s'en est retournè en Escosse’⁹⁾, mais le 1, le 14 et le 20 décembre¹⁰⁾ il parle de nombreuses conférences ‘depuis que nous nous sommes mis à perfectionner l'invention des Longitudes’ et même déjà de disputes sur le partage du profit. Bruce partit pour Londres vers le 1 janvier 1663 emportant avec lui ‘ses deux horologes pour les Longitudes’¹¹⁾. Il n'eut aucun succès: d'après sa lettre du 12 janvier 1663¹²⁾, quoiqu'il n'y eût pas eu de tempête, l'une des horloges était tombée et s'était détraquée, l'autre s'était arrêtée¹³⁾. Mais tant lui que Moray se proposaient de faire de nouveaux essais¹⁴⁾.

Nous publions à la fin du présent paragraphe la lettre du 19 janvier 1663 de Huygens à Bruce qui nous manquait et dont la copie nous parvint par les soins de M. Clifford Dobell (auteur de la brochure ‘The Kincardine papers’, Royal Society, London, Notes and Records, Vol. 4, mai 1947) tant de la part de la Royal Society que de la National Library of Scotland.

Ce fut Bruce qui avait amené Huygens à substituer un pendule court au long pendule¹⁵⁾. En outre Bruce avait doublé ‘la petite main par laquelle le pendule est mené’; ce pendule (dit à F renversé) est représenté à la p. 166 du T. XVII (à cela près que dans la figure le poids du pendule a la forme d'une lentille-année 1664- tandis qu'en 1662 il était globulaire); l'idée de suspendre l'horloge à une sphère d'acier enfermée dans un cylindre de cuivre était aussi de Bruce¹⁶⁾.

Sur la tige du pendule mentionné on remarquera le petit poids curseur servant à l'ajustement. Déjà en 1659 - nous l'avons dit aux p. 500 et 503 qui précèdent- Huygens avait su calculer la longueur d'un pendule mathématique isochrone avec un pendule également à verge impondérable mais portant, l'un au dessus de l'autre, deux

9) T. IV, p. 256.

10) T. IV, p. 274, 278 et 284.

11) T. IV, p. 281.

12) T. IV, p. 290.

13) Comparez la p. 193 du T. XVII.

14) T. IV, p. 318 et note 2 de la p. 168 du T. XVII.

15) Voyez les p. 160 et 161 du T. XVII.

16) Voyez la note de la p. 167 du T. XVII.

[p. 581]

poids punctiformes¹⁷⁾. À cet effet il était parti de l'hypothèse¹⁸⁾ que si l'on multiplie chaque poids par la hauteur maximale atteinte par lui au dessus d'un plan horizontal déterminé, la somme de ces produits sera la même dans le cas où les poids oscillent librement que dans celui où ils composent un corps unique: étant supposé bien entendu que dans le cas de l'oscillation dite libre les poids commencent à osciller (autour du même point de suspension) séparément, au lieu d'osciller conjointement, au moment où les deux poids se trouvent dans la situation la plus basse. C'est, comme Huygens le fait ressortir dans la Pièce de 1661 sur le centre d'oscillation¹⁹⁾, une application à ce mouvement réversible du grand principe - voyez la p. 509 qui précède - que le centre de gravité ne peut pas monter par la gravité seule²⁰⁾. Au lieu de supposer que les deux poids continuent à osciller après être devenus ‘libres’, on peut d'ailleurs aussi supposer²¹⁾ que les deux globes soient lancés dehors par la barre impondérable après avoir exécuté une demi-oscillation et s'élèvent verticalement par réflexion sur des surfaces planes chacun à sa plus grande hauteur; ou bien encore, comme le fait Huygens, qu'après une demi-oscillation le pendule soit réduit au repos par le fait que les deux globules, supposés parfaitement durs, entrent en collision avec des globes libres égaux du même genre qui (d'après la nouvelle théorie du choc) acquièrent chacun la vitesse entière du globe correspondant du pendule et s'élèvent, eux, chacun à la hauteur maximale (où ils sont arrêtés) par la dite réflexion idéale. Ce principe peut évidemment servir aussi dans le cas où le nombre des poids est supérieur à deux; déjà en 1659 Huygens en avait fait usage en considérant le cas où la barre oscillante n'est pas impondérable mais composée d'une infinité de poids égaux infiniment petits; cette barre pouvant en outre porter, par exemple à son extrémité, un seul globule punctiforme, mais possédant un poids fini. La dispute avec Douw et d'autres horlogers²²⁾ - nous l'avons dit à la p. 503 - avait activé cette recherche du centre d'oscillation déjà préconisée dix ans plus tôt par Mersenne²³⁾. Les p. 105-112 du T. XVII contiennent les calculs de 1661 sur le poids curseur qui se rattachent à ceux de 1659; les p. 414-433 du T. XVI, également de 1661, y font suite; tous ces calculs datent du mois d'août ou plutôt septembre et des mois suivants. Bruce y était étranger tout autant qu'aux considérations sur l'inégalité des jours. Voyez sur ce

17) P. 354 et 387 du T. XVI.

18) T. XVI, p. 387, note 5, dernier alinéa.

19) ‘De centro oscillationis sive ad invenienda perpendicula simplicia isochrona propositis perpendiculis compositis’, p. 145 et suiv. du T. XVI.

20) Voyez aussi sur ce sujet la p. 21 du T. XVI.

21) T. XVI, p.414, note 3.

22) Comparez la note 3 de la p. 105 du T. XVII.

23) P. 426 qui précède.

[p. 582]

dernier sujet le T. XV²⁴⁾. Lorsque Bruce quitta la Haye, Huygens avait déjà l'intention²⁵⁾ d'écrire une instruction au sujet de l'emploi des horloges pour trouver les longitudes, y compris un chapitre sur la méthode de mesurer la hauteur du soleil²⁶⁾.

Ce ne furent pas là cependant les premiers sujets auxquels Huygens s'appliqua après sa rentrée du 27 mai 1661 à la Haye.

Dès le 15 juin il observa de nouveau la planète Saturne²⁷⁾. Ses lettres de septembre²⁸⁾ et décembre 1661 à Moray, et bien d'autres lettres, font voir combien il continuait à s'y intéresser. Consultez sur ce sujet les p. 476-477 du T. XV.

Signalons aussi son intérêt pour la publication de 1662 du ‘Venus in sole visa’ de Horrox²⁹⁾.

On a vu qu'en passant à Anvers il avait entendu des carillons. Ce fut, pensons-nous, à sa demande qu'un ami lui envoya de là, le 16 juin, la copie d'une page flamande- on ne la connaît pas d'ailleurs - d'un des frères Hemony, fondeurs et installateurs des dits carillons²⁸⁾; elle traite de la ‘règle de l'accord, comment celui-ci est trouvé par la proportion numérique’. L'ayant lu il écrivit le 8 juillet suivant la Pièce intitulée ‘Divisio monochordi’ où il se sert de ‘termini Algebraici systematis indeterminati³⁰⁾’: partant d'une corde de longueur a il calcule les longueurs des cordes dont les tons forment avec le ton fondamental les intervalles du système pythagoricien; posant x pour la longueur de la corde correspondant à la quinte du ton fondamental, de sorte que le rapport x/a de l'intervalle fondamental de la construction pythagoricienne reste momentanément indéterminé, il déduit tous les tons du système du ton fondamental, à l'instar d'Hemony, par des sauts de quintes et de tierces avec réduction d'octaves.

24) P. 523-526 et 553-557, Pièce VI, à laquelle se rattachent plus ou moins les Pièces VII et VIII.

25) Voyez l'Appendice à la p. 236 du T. XVII.

26) Voyez la p. 197 du T. XVII qui renvoie au T. XV.

27) T. XV, p. 74.

28) P. 71 qui précède.

29) Voyez e.a. les p. 314 du T. III et 27 du T. IV. Nous rappelons qu'à Londres Huygens avait observé une transition de Mercure.

28) P. 71 qui précède.

30) T. XX, p. 57. La Pièce entière y occupe les p. 49-58.

[p. 583]

Alors seulement il se demande ‘quanta convenientissime possit statui x’. Si l'on prend x = 2/3 a, toutes les quintes et quartes sont parfaites; il n'en sera pas de même des tierces et des sixtes. On peut aussi postuler la justesse de la tierce majeure, ce qui conduit à 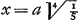, ou bien que les quintes soient inférieures d'autant que les sixtes majeures soient superieures à leurs vraies valeurs, ce qui conduit à la même valeur 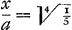; c'est le système dit du ton moyen auquel Huygens donne le nom de ‘temperament veritable’.

C'est également de 1661³¹⁾ que date la Pièce ‘Divisio octavae in 31 intervalla aequalia’ où les calculs sont exécutés ‘per logarithmos’ ce qui ne peut guère se faire autrement comme Huygens le relève dans sa lettre à Moray du 1 août³²⁾. L'avantage du nouveau tempérament auquel correspond cette division en 31 intervalles c'est que la περιϰύϰλωσις de Stevin, ou d'Aristoxène, obtenue par la division de l'octave en 12 intervalles égaux, y est conservée³³⁾ sans que les écarts des tons avec ceux du ‘temperament veritable’ soient aucunement considérables. En ce temps Huygens ne songea pas à rien publier sur ce sujet. Il a pu savoir qu'en 1659 Rembrantz. van Nierop avait critiqué Stevin³⁴⁾ qui ne considérait pas la dite division en 12 intervalles égaux comme un tempérament, étant d'avis qu'elle correspond à la nature des tons; en quoi Huygens est pleinement d'accord tant avec van Nierop qu'avec feu Descartes³⁵⁾.

En majeure partie les Pièces du portefeuille ‘Musica’ ne sont pas datées. Nous croyons cependant pouvoir dire que la Pièce publiée en partie dans le T. XIX sous le titre ‘Rapports des longueurs des cordes consonnantes suivant Pythagore, et rapports des nombres de leurs vibrations suivant Galilée et d'autres savants’³⁶⁾ et en partie dans le T. XX sous le titre ‘Origine du chant. Rapports des longueurs etc.’³⁷⁾ date de ce temps³⁸⁾, quoique le paragraphe sur Galilée puisse y avoir été ajouté plus

31) Voyez les p. 147 et 205 du T. XX.

32) Citée à la p. 12 du T. XX.

33) Voyez la p. 143 du T. XX.

34) Dans la brochure que nous avons citée à la p. 187 du T. XXI.

35) Consultez la note 9 de la p. 32 du T. XX où l'on voit que déjà Descartes - et Beeckman (qui avait d'abord suivi Stevin) avant lui - étaient d'avis qu'il ne faut pas nier avec Stevin ‘qu'il y ait de la difference entre les demitons’.

36) T. XIX, p. 361-363.

37) T. XX, p. 30-37.

38) Nous avons dit aux p. 28-29 du T. XX pourquoi cette Pièce nous semble antérieure à la conversation de Huygens avec un des frères Hemony à Amsterdam. Or, cette conversation eut lieu en août 1662. Il est sans doute possible que la Pièce soit plus ancienne de quelques années, qu'elle date p.e. de 1659. En 1659 Huygens avait fait une expérience avec une ‘chorda campanae consona’ (T. XVII, p. 265 et 339).

[p. 584]

tard. Quant à la trompette marine³⁹⁾, mentionnée en marge (à propos de la question de savoir si le nombre 7, comparé à d'autres, est capable de produire une bonne consonance), Huygens avait appris à la connaître, semble-t-il, à Paris chez la famille Petit⁴⁰⁾.

Le calcul logarithmique dont nous venons de parler le conduisit tout de suite- ceci aussi déjà avant qu'il s'occupât des pendules et des horloges - à mieux considérer les logarithmes. Il se servait de tables logarithmiques au moins depuis 1657⁴¹⁾ mais ce ne fut qu'en juillet 1661⁴²⁾ qu'il se mit vraiment ‘a considerer ces merveilleux nombres’; en ce même mois il déduisit, en partant d'une considération mathématique de Grégoire de St. Vincent sur l'hyperbole, une règle pratique pour les calculer; on la trouvera dans notre T. XIV⁴³⁾. Elle fut suivie, en septembre, par la construction, par points, de la courbe logarithmique⁴⁴⁾ - voyez ce que nous disons un peu plus loin sur la construction de 1652 - dont il constata l'invariabilité de la longueur de la soustangente⁴⁵⁾. Les points sont en nombre infini, et Huygens suppose qu'il en résulte une courbe continue, sans quoi il ne pourrait parler d'une tangente ou soustangente. On pourrait dire aussi que la constance de la soustangente (le ‘latus rectum’) définit une courbe continue. Mais c'est ce que Huygens ne dit pas. La longueur de la soustangente, si elle n'est pas prise pour point (ou plutôt pour ligne) de départ, ne peut être trouvée ‘ratione ulla geometrica sed ex logarithmis quamlibet proximè’⁴⁶⁾. En 1667 Mercator écrira: ‘Est logarithmus nihil aliud quam numerus ratiuncularum contentarum in ratione quam absolutus quisque [numerus] ad unitatem obtinet’⁴⁷⁾. Dans la courbe continue considérée par Huygens⁴⁸⁾ il ne peut être question de ratiunculae finies, quelque petites - nous voulons dire: quelque peu supérieures à l'unité- qu'on les suppose. Les logarithmes, lorsqu'on part de cette courbe, sont, nous semblet-il, des nombres infiniment grands, représentés par des lignes de longueur finie, ou

39) Qui n'est pas une trompette.

40) Le 30 janvier 1661, voyez la p. 550 qui précède.

41) Consultez la p.619 du T. XX.

42) D'après la lettre à Moray du 1 avril citée à la p. 12 du T. XX.

43) P. 411-434 et 451-457.

44) T. XIV, p. 439-442 et 460-471.

45) Elle est calculée, approximativement, par la considération de ce qu'on appela un peu plus tard le triangle caractéristique.

46) L. 1 de la p. 464 du T. XIV.

47) Nous avons cité cette définition à la p. 11 du T. XX.

48) La continuité d'une ligne ou d'un mouvement est apparemment suivant Huygens une propriété qu'on peut et doit admettre sans contestation; mais il n'y a pas de continuité dans les nombres (ce qui paraît contraire au sentiment d'Aristote); comparez les p. 371-372 du T. XX.

[p. 585]

bien plutôt des longueurs finies correspondant à des nombres infiniment grands. Huygens ne parle pas de nombres infiniment grands; il se contente de faire voir que le rapport des valeurs de deux logarithmes, c.à.d. de deux longueurs, est obtenu d'autant plus ‘accuratius’ que les nombres qui les expriment sont plus grands.

Il fait voir en outre qu'on peut parfois obtenir, sur l'égalité de certains espaces, des résultats exacts par un raisonnement, à son avis irréprochable, autre que la réduction archimédienne à l'absurde⁴⁹⁾.

Il faut d'ailleurs observer que déjà en 1652, sans parler de logarithmes, il avait tracé, ou plutôt conçu, pour représenter une série géométrique, une courbe qui n'est autre que la logarithmique⁵⁰⁾. La Pièce de 1661 (?) des p. 291-294 du T. XX, où il est fait usage de logarithmes, s'y rapporte.

Notons encore, à propos de la notion de la continuité, que Huygens condamne toute théorie qui suppose de la discontinuité dans l'écoulement du temps⁵¹⁾.

On voit que, quoique Huygens eût écrit à Moray le 15 juillet 1661: ‘Je vous assure que j'ay encore du travail assez pour longtemps, à mettre au net plusieurs de mes vieilles inventions et quelques traités à demi achevez que j'ay [l'idée] de perfectionner et de produire’, il ne put s'empêcher de s'intéresser à de nouveaux sujets, au point que le dit achèvement et perfectionnement ne purent venir à l'ordre du jour.

Il est possible qu'ayant récemment reçu une description de la machine à voler polonaise⁵²⁾ il ait essayé de construire, comme il pensait pouvoir le faire⁵³⁾, pareil avion, ou plutôt un automate ‘a l'exemple du bon Archytas’. Nous pouvons du moins difficilement nous figurer que la reconstruction du pigeon d'Archytas rapportée, sans bonne description, aux p. 316-318 qui précèdent, daterait réellement de 1692.

49) P. 466 du T. XIV.

50) Nous l'avons dit aussi à la p. 204 du T. XX.

51) Lettre à Moray de septembre 1661, T. III, p. 320.

52) Voyez les p. 425 et 427 qui précèdent.

53) Lettre du 21 juillet 1661 à Thévenot.

[p. 586]

Une autre étude vint s'ajouter dès septembre 1661, ou déjà plus tôt, à celles dont nous venons de parler: la construction d'une machine pneumatique et l'examen de divers phénomènes dans le vide. Huygens en énumère quelques-uns⁵⁴⁾, n'oubliant ni les larmes de verre dont il fut question plus haut⁵⁵⁾ et auxquelles on s'intéressait tant à Paris⁵⁶⁾ qu'à Londres⁵⁷⁾, ni la mystérieuse ascension de l'eau dans les petits tuyaux que Rohault avait exhibés à Paris⁵⁸⁾ et dont on avait discuté à Gresham's College⁵⁹⁾. Il est possible que la courte Pièce sur la nature de l'eau où les petits tubes sont également mentionnés⁶⁰⁾ date de ce temps. C'est en Angleterre que Huygens avait vu la pompe à air de Boyle, de qui il avait de plus reçu un article sur l'ascension de l'eau dans les petits tubes et sur les autres phénomènes que nous appelons capillaires⁶¹⁾; notre Avertissement des p. 258-264 du T. XVII se rapporte à cette pompe; à Paris il n'avait peut-être été question que de pompes à compression⁶²⁾ - sujet dont Huygens s'était occupé; même Avertissement - et du vide d'air obtenu par écoulement d'eau⁶³⁾. Cet Avertissement fait voir aussi que Christiaan tenait son frère Lodewijk au courant. Celui-ci, revenu d'Espagne et parti pour Paris avec le père Constantyn après un bref séjour à la Haye, fut par Christiaan mis en rapport avec diverses personnes qu'il y avait connues et auxquelles il recommande de faire connaître ses expériences. Lodewijk resta à Paris jusqu'en février 1663.

D'ailleurs Christiaan continuait à correspondre directement avec ses amis français. - Voyez sur des horloges envoyées à Paris la note 5 de la p. 158 du T. XVII. - Dans la lettre à Chapelain du 14 juillet 1661, laquelle se rattache à celle à de Montmor (?) de la p. 76 qui précède, il écrit: ‘Vous scauez quel est le dessein de ces Messieurs là [les membres de la Royal Society] à scavoir de s'attacher plus a faire des experiences que des raisonnements’ etc.

Nous avons ajouté une traduction française à la Pièce néerlandaise du Manuscrit B où Huygens nota ses expériences du vide, lesquelles durèrent du 29 novembre 1661 au 20 février 1662 - ce dernier jour il détermina le poids de l'air -, une reconstruction de l'appareil étant encore rapportée en octobre 1662⁶⁴⁾. Mais déjà depuis 1661 la machine de Huygens se distinguait de celle de Boyle en un point important;

54) T. XVII, p. 307.

55) P. 518.

56) Expérience de Rohault du 17 mars 1661.

57) Le 6 avril 1661.

58) Le 7, le 14 et le 21 décembre 1661.

59) Le 20 avril 1661.

60) T. XVIII, p. 333-334.

61) T. III, p. 328.

62) Le 6 janvier 1661.

63) Le 13 novembre 1660.

64) T. XVII, p. 312-333.

[p. 587]

l'écuelle du récipient inventée par lui. Huygens n'accepta la loi de Boyle, d'après laquelle le ressort de l'air s'affaiblit à mesure qu'il s'étend, que lorsqu'il eut reçu en juillet 1662 son traité sur ce sujet. Cette loi ne donnait pourtant pas l'explication du curieux phénomène découvert par Huygens vers la fin de 1661: il constata que l'eau contenue dans un tube renversé ne descend pas lorsqu'on évacue le récipient (comme il semblait qu'elle devrait toujours faire) dans le cas où cette eau est bien purgée d'air. Ce phénomène de Huygens - nous continuerons à le désigner par ce terme - donna lieu à bien des débats. Il en avait fait part à Moray dans une lettre du commencement de février 1662⁶⁵⁾ et au frère Lodewijk, pour le communiquer à Thévenot et d'autres, le 15 du même mois⁶⁶⁾. Provisoirement il n'en donna lui-même, après avoir appris à connaître et approuvé la loi de Boyle, aucune explication.

Notons en passant la reproduction par Huygens⁶⁷⁾, en 1662, de l'engrenage - nous pourrions dire: l'engrenage de Schwenter - servant à hausser de l'eau p.e. dans les mines.

Lodewijk, à son tour, donnait de Paris des informations sur ce qui pouvait intéresser ses frères. C'est ainsi qu'il fit connaître à Christiaan⁶⁸⁾ la célèbre démonstration de Fermat sur la loi des sinus, basée sur un principe que Christiaan qualifie d'abord de pitoyable, ensuite - voyant que dans ce cas au moins il conduit à une conséquence remarquable - de fort précaire: c'est, pour parler avec Fermat⁶⁹⁾, ‘ce principe si commun & si estably que la nature agit tousjours par les voyes les plus courtes’.

C'est alors - nous l'avons dit à la p. 267 du T. XVIII - que Huygens peut avoir acquis la conviction que l'indice de réfraction est égal au quotient de la vitesse de la lumière dans le premier milieu par celle de la lumière dans le second.

Il continua en 1662 ses recherches sur les couronnes et parhélies. Il est possible que son manuscrit en grande partie néerlandais, tel que nous l'avons publié en 1932,

65) T. IV, p. 23.

66) T. IV, p. 53.

67) P. 201 qui précède.

68) T. XVII, p. 266 et 340.

69) T. IV, p. 76.

[p. 588]

fut achevé avant la fin de cette année⁷⁰⁾. Nous aurions pu mentionner déjà dans un chapitre précédent l'expérience de 1659 du cylindre de verre, rempli d'eau, à noyau de bois, dont il y est question⁷¹⁾, ainsi que la condamnation, en ce même temps, du grand cercle de glace de Descartes⁷²⁾. On peut voir dans l'Appendice XI au traité que le cylindre de verre représentait un cylindre de glace transparente à noyau opaque. De pareils cylindres, évidemment exigus, et aussi de petits grains de glace ronds à noyaux sphériques opaques, étaient nécessaires à son avis pour produire les effets observés: il pensait en ce temps⁷³⁾ que les couleurs s'engendrent à la limite de la lumière et de l'ombre, de sorte que les rayons, pour les produire, doivent friser des noyaux opaques.

Toujours occupé à tailler des lentilles pour les grandes lunettes - voyez e.a. sur les grandes lunettes qu'on se proposait de construire, ou qu'on possédait déjà, en Angleterre, à Danzig et en Pologne, diverses pages du T. III⁷⁴⁾ - Huygens fit construire à cet effet, au début de juin 1662, une machine portative d'après un modèle récent provenant de lui-même et du frère Constantyn qui en ces années fut constamment à la Haye. C'est, pensons-nous, la machine représentée à la p. 301 du T. XVII⁷⁵⁾. Malheureusement elle ne satisfit pas quoique Christiaan la dise ‘aussi bien inventée qu'elle scauroit estre’⁷⁶⁾. Il en conclut un peu hâtivement qu'aucune machine ne peut servir si ce n'est celle du bâton avec la pointe⁷⁷⁾ qui à proprement parler, dit-il, n'en est pas une.

Hâtivement, disons-nous, puisque dans les années suivantes les frères construisirent néanmoins encore diverses machines: voyez les figures des p. 302-304 du T. XVII, dont la première au moins est certainement de 1665. Consultez aussi ce qu'écrit Spinoza⁷⁸⁾ sur la ‘fabrica satis nitida’ qu'il vit en cette année. Quoique ces machines à apparence ‘nitida’ ne donnassent toujours pas les résultats espérés. Il semble possible

70) Voyez la p. 359 du T. XVII.

71) Note 37 de la p. 486 du T. XVII et déjà antérieurement à la p. 473.

72) T. XVII, p. 454, l. 13-14.

73) Voyez notre note 12 de la p. 356 du T. XVII.

74) Les p. 179, 285, 293, 294.

75) Fig. 24 et 25 de cette page; consultez-y les notes 3 et 4.

76) Lettres à Lodewijk du 1 et du 15 juin, T. IV, p. 144 et 152.

77) Fig. 21 de la p. 299 du T. XVII.

78) P. 12 qui précède.

[p. 589]

- mais nous ne croyons pas qu'il faille dire probable, comme le fait G. Tierie⁷⁹⁾ - que cette persévérance soit due à l'influence du père Constantyn affirmant que Drebbel fabriquait jadis des lentilles de cette manière. Puisque le père Constantyn s'était rendu à Paris déjà en octobre 1661 et qu'il appert par la lettre de Christiaan que Lodewijk qui avait quitté la Haye en même temps, n'avait probablement rien entendu à la maison paternelle d'un pareil projet de ses frères, nous croyons en tout cas pouvoir dire que la construction de la première machine n'était pas due à l'initiative du père.

La construction des lunettes à la Haye par les frères Huygens fut apparemment continuelle; il est souvent question dans les lettres à lodewijk (celles de L. font défaut) de petits miroirs d'acier destinés à ces lunettes⁸⁰⁾ - les petits miroirs redressaient les images - ou du moins de minces plaques d'acier, fournies par P. Petit, devant servir à y découper les miroirs. Une de ces lunettes, de dimensions modestes, fut envoyée en mai 1662 à Paris au maréchal de Grammont⁸¹⁾. Le père Constantyn y avait apporté une dont il avait fait cadeau - comme il le fit aussi d'une horloge - à Louis XIV⁸²⁾. Nous avons déjà dit un mot, à la p. 522 qui précède, sur Constantyn à la cour du Roi-Soleil.

Soit dit entre parenthèses, le but principal pour lequel le père Constantyn s'était rendu à Paris, c'était de poursuivre les négociations relatives à la restitution au jeune prince Willem de la Principauté d'Orange; lesquelles n'eurent du succès qu'après

79) G. Tierie, ‘Cornelis Drebbel (1572-1633)’, H.J. Paris, Amsterdam. 1932, p. 48-49: ‘It is very probable that Constantyn Huygens also learned the art of glass grinding with a machine from Drebbel in 1622 when he was in close contact with the latter, and then later taught it to his son Christiaan’. Les expression ‘learned the art’ et ‘taught it’ sont certainement trop fortes. Constantyn ne dit nulle part avoir rien vu ou entendu de Drebbel sur ce sujet. Il est cependant difficile de nier que, comme le dit de Peiresc sur l'autorité d'un des gendres de Drebbel (manuscrit cité par F.M. Jaeger dans ‘Cornelis Drebbel en zijn tijdgenooten’. P. Noordhoff, Groningen, 1922), Drebbel puisse avoir eu ‘en sa maison près de Londres’ un ‘moulin qui fait les verres sur la proportion qu'on desire’, moulin qu'on peut ‘faire aller par un petit garçon’, ou du moins un appareil de ce genre, et que Christiaan peut l'avoir su par oui-dire: dans les ‘Sermones de vita propria’ le père Constantyn parle de ‘multi sermones’ de Drebbel, de ‘multas horas’ passées avec lui. Voyez aussi sur l'intérêt du père Constantyn pour la fabrication des lentilles la p. 248 du T. XVII.

80) Comparez la note 22 de la p. 455 qui précède; cette note renvoie à la p. 266 du T. XIII où se trouve une figure des lunettes à miroir.

81) T. IV, p. 100 et 136.

82) T. IV, p. 92. Voyez pour l'horloge la p. 389 du T. III.

[p. 590]

quelques années, de sorte qu'il ne rentra à la Haye qu'en juin 1664. Mais ces négociations tombent en dehors du cadre de la biographie de Christiaan telle que nous la concevons.

L'invention du célèbre oculaire de Huygens, nous l'avons dit plus haut⁸³⁾, date apparemment de 1662: le 5 octobre il écrit à Lodewijk: ‘pour les oculaires, vous voyez bien que j'y ay trouuè quelque chose de nouueau, qui cause nettetè dans les lunettes du jour, et de mesme dans les plus longues, leur donnant en mesme temps une grande ouverture’. Voyez sur cet oculaire notre T. XIII aux endroits indiqués dans la Table des Matières traitées. Des expériences pour regarder des lettres de loin sont rapportées dans la dite lettre à Lodewijk.

Vers la fin de 1665 Huygens commença à travailler à une lunette de 60 pieds⁸⁴⁾.

Les logarithmes, en 1662, purent être employées par Huygens dans une partie des calculs relatifs aux couronnes et parhélies, lesquels nous avons réunis dans l'Appendice X au dit traité⁸⁵⁾. Une partie de ces calculs⁸⁶⁾ est d'ailleurs antérieure à 1662.

Autre application des logarithmes. Aussitôt qu'en juillet 1662 il s'était convaincu de la justesse de la loi de Boyle - il en avait d'abord douté⁸⁷⁾ - il comprit la possibilité de déduire de cette loi ce qu'il appelle la hauteur de l'atmosphère, c.à.d. la loi suivant laquelle la densité doit décroître à mesure qu'on s'élève⁸⁸⁾. Conformément à son habitude il ne publia pas ce calcul, se bornant à faire connaître à ses amis quelques résultats numériques⁸⁹⁾.

Voilà bien de la physique mathématique. L'on voit que suivant Huygens - quelque

83) P. 454.

84) Voyez les premières lettres du T. VI.

85) Cet Appendice occupe les p. 478-496 du T. XVII. Voyez-y des logarithmes aux p. 480, 481, 484, 488 et 489.

86) Mais dans cette partie il n'est pas fait usage de logarithmes.

87) Voyez la p. 253 du T. XVII.

88) T. XIV, p. 436-438 et 483-494. Il est vrai qu'il écrit que lorsque la densité devient très faible, la loi de Boyle pourrait bien ne plus être vraie.

89) Lettres à Moray; voyez les p. 202, 205-206 et 217 du T. IV.

[p. 591]

convaincu qu'il soit de la réalité des atomes - il est possible d'obtenir par le calcul sur certaines grandeurs mesurables des résultats de valeur sans passer par la considération des particules, même lorsqu'il ne s'agit pas de corps solides ou liquides, où cette vérité est évidente, mais de l'air.

Il essaya cependant de comprendre plus ou moins la loi de Boyle en s'imaginant comme lui⁹⁰⁾ que l'air consiste ‘ex corporeis partibus sese mutuo tangentibus’ d'où résulte une ‘vis elastica’⁹¹⁾. Cette image ne correspond pas à ce que disait Descartes dans le passage des ‘Principia philosophiae’ que nous avons cité à la p. 320 du T. XIX: ‘aërem nihil aliud esse debere, quam congeriem particularum tertii elementi tam tenuium, & à se mutuò disjunctarum [nous soulignons], ut quibuslibet motibus globulorum coelestium obsequantur’. Elle ne correspond pas non plus à un passage de Huygens dans le ‘Traité de la lumière’ de 1690⁹²⁾ d'après lequel la ‘penetrabilitè [de l'air] qui luy demeure non obstant sa compression, semble prouver qu'il est fait de petits corps qui nagent & qui sont agitez fort viste dans la matiere etherée, composée de particules bien plus petites’ ce qui est plus ou moins la conception cartésienne. En 1668 aussi il disait⁹³⁾ que grâce au ‘remouement’ due à la matière subtile - la matière subtile de 1667, p. 553 du T. XIX - les parties de l'air ‘voltigent’. Nous constatons ici que telle n'était pas l'opinion de Huygens en 1662. L'expérience de la vessie à peu près vide qui dans le vide se gonfle, laquelle était de l'invention de Roberval⁹⁴⁾ et qui avait été proposée à Huygens par Mersenne⁹⁵⁾ avait en 1648 été expliquée par lui simplement par le fait que ‘l'air qui est restè dans la vessie est contraint de se dilater pour estre également distribuè par tout l'espace vuide, tant qu'il est possible’. On dirait que dans sa jeunesse - quoiqu'en 1648 on eût pu le supposer entièrement sous l'influence de Descartes - il ne songe pas à un mouvement de particules plus fines agissant sur celles de l'air; il est vrai qu'il n'apparaît pas d'où résulterait donc la dite contrainte. Rien sans doute n'indique qu'il aurait songé à un mouvement spontané des particules de l'air (quoique déjà en 1648 il montre son indépendance de Descartes en parlant du vide). En 1662, comme nous l'avons vu, il se contente de la conception - de l'hypothèse de travail, pourrions-nous dire - de particules élastiques entassées; on peut se figurer ces particules élastiques comme des ‘ressorts entortillez’⁹⁶⁾.

90) Nous l'avons dit aussi dans la note 13 de la p. 343 du XVII.

91) T. XIV, p. 485.

92) T. XIX, p. 471.

93) T. XVI, p. 186 et T. XIX, p. 6.

94) T. XVII, p. 262.

95) P. 427 qui précède.

96) P. 185 du T. XVI.

[p. 592]

Un jour avant cette application-là, le 15 juillet 1662, Huygens avait de nouveau considéré les rapports entre les logarithmes et l'hyperbole⁹⁷⁾: il avait obtenu par les logarithmes la quadrature approchée d'un espace hyperbolique quelconque, ainsi que la rectification approchée d'un arc quelconque de parabole qui en dépend.

En septembre 1662 Huygens écrivit la remarquable Pièce sur la rupture d'une poutre soutenue en deux endroits: il y étend hardiment, et avec succès, le principe d'après lequel le centre de gravité descend autant que possible, au cas où la poutre se brise⁹⁸⁾. Voyez sur ce sujet l'Avertissement correspondant⁹⁹⁾, où nous nous sommes étendu de plus sur une autre particularité de cette Pièce, savoir la conception moderne du ‘momentum’ comme produit d'un poids par une distance, et plus généralement sur la formation du style de la mécanique classique. Récemment cet Avertissement a encore donné lieu à un article dans la revue ‘Faraday’¹⁰⁰⁾.

La correspondance avec de Sluse et d'autres donna lieu en cette même année à quelques autres considérations géométriques qu'on peut voir au T. XIV. Il y est question (outre de l'heptagone régulier) de constructions de tangentes à certaines courbes. Quelques-unes des méthodes de Huygens peuvent être qualifiées de curieuses¹⁰¹⁾. Bientôt après il trouva une méthode générale, la tangente à une courbe d'équation donnée étant déterminée pour chaque point par le calcul de la longueur de la soustangente; il s'agit ici - autrement que dans le cas de la courbe logarithmique (dont la soustangente avait été trouvée constante) - de ‘courbes geometriques’ ou, comme nous dirions, algébriques, c.à.d. de courbes représentées par des équations ne contenant que des puissances entières des deux coördonnées (x et y). Il réussit à exprimer z (la soustangente) en fonction de x et de y. C'est cette méthode que Huygens expose dans sa Pièce de février 1663 à Joh. de Witt¹⁰²⁾. S'il eût voulu, il eût pu y ‘parler de Fermat, de Hudde et de Slusius¹⁰³⁾.’

97) T. XIV, p. 434-435 et 474-482.

98) T. XVI, p. 381-383.

99) T. XVI, p. 333-343.

100) Livraison de juin 1948. On y trouvera, à propos de la question de la genèse des formules de physique, outre le nom de Huygens, ceux d'Aristote, de Galilée et de Wallis: comparez la p. 459 qui précède. L'article est intitulé: ‘De uitvinding van de natuurkundige formule’, par D. Burger et J.A. Vollgraff.

101) T. XIV, p. 508, note 5.

102) Elle avait été précédée, d'après la lettre 1100 du T. IV, par une exposition orale.

103) Voyez les p. 210 et 243 du T, XX, ainsi que la p. 315 du T. VII où il dit: ‘C'est pourtant Monsieur Hudde qui m'en a monstrè la pratique’.

[p. 593]

Enfin nous signalons la réponse, de décembre 1662, à une critique de Hobbes qui fut lue et approuvée à la Royal Society¹⁰⁴⁾.

Voici la lettre à ‘Brus’ dont il était question à la p. 580.

104) T. IV, p. 281 et 295.