Oeuvres complètes. Tome XIX. Mécanique théorique et physique 1666-1695

[p. 407]

I.
La refraction double du cristal d'islande.
[1672 ou 1673]¹⁾

Chrystalli Islandicae refractio duplex mirabilis [Fig. 127].

§ 1. Perpendiculariter incidens refringitur [Fig. 128].

Non facit duplicem reflexionem.

[Fig. 127.]
Les lettres r o désignent apparemment les rayons réguliers et irréguliers (regelmatig, onregelmatig) provenant d'un point du cristal ou d'un objet placé dans le voisinage immédiat de sa surface horizontale inférieure.

[Fig. 128.]
On voit déjà dans cette figure en crayon les ondes obliques par rapport à la direction des rayons réfractés. Voyez cependant aussi la Fig. 136 qui suit.

Les angles obtus qui font l'angle solide O [Fig. 131] estans chacun de 101 degr. il s'en suit²⁾ que l'angle de l'inclination de 2 surfaces qui aboutissent a cet angle comme GOCA, FOCB, est de 103.40′. Il s'en suit aussi²⁾ que l'angle que le costè OC [fait] avec la ligne CI qui coupe l'angle BCA en deux parties egales, sera de 72.34′.

1) La Pièce est empruntée au Manuscrit D, p. 348-358. Elle doit dater de 1672, ou peut-être de 1673, puisque la p. 359 porte la date de décembre 1672 et la p. 339 celle du 10 juin 1673. Comparez la note 4 de la p. 413.

2) Voyez sur Erasmus Bartholinus la note 1 de la p. 258 du T. I et la note 7 de la p. 518 du T. V. Pendant son séjour en Hollande Huygens entra en relations avec lui (T. I, p. 491, 495). Il lui envoya en 1658 un exemplaire de l'‘Horologium’ (T. II, p. 209). La présente Pièce fait voir que Huygens connaissait en 1672 (ou 1673) les ‘Experimenta crystalli islandici disdiaclastici quibus mira & insolita refractio detegitur’, publiés en 1669-1670 (l'exemplaire de la Bibliothèque de l'Université de Leiden porte la date 1670, non pas 1669) par E. Bartholinus à Copenhague. Bartholinus avait plusieurs frères; c'est peut-être parce qu'il ne se rappelait pas bien le prénom de son ancienne connaissance (il est d'ailleurs douteux s'il l'ait connu personnellement) que Huygens demanda en novembre 1677 (T. VIII, p. 41) à Römer - qui tâchait lui aussi d'expliquer la double réfraction (T. VIII, p. 46) - ‘quisnam sit ille Bartholinus’. Bartholinus calcule, en partant de l'angle mesuré de 101^o, les angles de 103^o40′ et 72^o34′, mais sans se servir de triangles sphériques (voyez la fin de la note 3).

2) Voyez sur Erasmus Bartholinus la note 1 de la p. 258 du T. I et la note 7 de la p. 518 du T. V. Pendant son séjour en Hollande Huygens entra en relations avec lui (T. I, p. 491, 495). Il lui envoya en 1658 un exemplaire de l'‘Horologium’ (T. II, p. 209). La présente Pièce fait voir que Huygens connaissait en 1672 (ou 1673) les ‘Experimenta crystalli islandici disdiaclastici quibus mira & insolita refractio detegitur’, publiés en 1669-1670 (l'exemplaire de la Bibliothèque de l'Université de Leiden porte la date 1670, non pas 1669) par E. Bartholinus à Copenhague. Bartholinus avait plusieurs frères; c'est peut-être parce qu'il ne se rappelait pas bien le prénom de son ancienne connaissance (il est d'ailleurs douteux s'il l'ait connu personnellement) que Huygens demanda en novembre 1677 (T. VIII, p. 41) à Römer - qui tâchait lui aussi d'expliquer la double réfraction (T. VIII, p. 46) - ‘quisnam sit ille Bartholinus’. Bartholinus calcule, en partant de l'angle mesuré de 101^o, les angles de 103^o40′ et 72^o34′, mais sans se servir de triangles sphériques (voyez la fin de la note 3).

[p. 408]

[Fig. 129.]

ACB	101.0′ } Bartholino [Fig. 131 et 131 bis].
BCO	79.0′ } Bartholino [Fig. 131 et 131 bis].
BCD	50.30′ } Bartholino [Fig. 131 et 131 bis].
DXB	51.50′ } Bartholino [Fig. 131 et 131 bis].
AXB	103.40′ } Bartholino [Fig. 131 et 131 bis].
DCX	72.34′ } Bartholino [Fig. 131 et 131 bis].

[Fig. 130.]

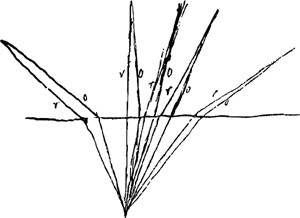
Refractio Chrystalli Islandicae proximè quae 5 ad 3, saltem non major. Haec nempe est illa refractio quae legibus solitis paret [Fig. 129]¹⁾.

La Fig. 130 représente une réfraction régulière: les ondes y sont perpendiculaires aux rayons.

Anguli inclinationis superficierum 105 gr. Anguli obtusi superficierum circiter 101 unde acuti 89 [lisez 79]²⁾.

1) Bartholinus (p. 40) dit déjà, en parlant de la réfraction ordinaire, ‘refractionis hujus crystalli rationem insensibiliter aberrare à ratione 5 ad 3.’

2) Cet alinéa a apperemment été ajouté plus tard, lorsque Huygens eut compris que pour trouver la valeur exacte de l'angle ACB il valait mieux commencer par mesurer l'angle solide auquel, dans le Traité de la Lumière aussi, il donne la valeur précise de 105^o; d'où résulte pour ACB la valeur 101^o52′ (p. 522 qui suit). En 1677 (p. 430 qui suit) Huygens donne à l'angle ACB les valeurs 101^o18′, 101^o27′, 101^o30′ et à l'angle solide celle de 104^o6′; il semble qu'en cette année seulement il commence à se servir du triangle sphérique qui donne la relation entre les deux angles, quoiqu'en général il se soit servi de triangles sphériques longtemps avant ce temps (voyez aux p. 478-496 du T. XVII l'Appendice X au Traité des Couronnes et des Parhélies).

[p. 409]

[Fig. 131 et 131 bis]
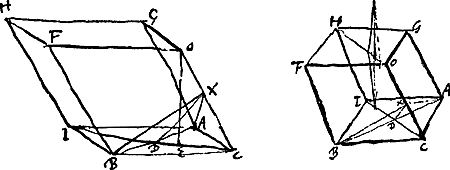
La Fig. 131 est une copie par Huygens d'une figure de Bartholinus.

§ 2. Ce cristal est une espece de talc tres clair et transparant sans aucune couleur. Il croist en Islande et l'on en trouve d'assez gros morceaux. Le.... (?) de ceux que M. Picard a apporté de Dannemarc³⁾ avoit bien 6 a 7 pouces de long, et trois pouces de hauteur et autant de largeur.

La dureté est comme celle de l'albastre, de sorte qu'une pointe de fer l'entame facilement.

Il a la forme d'un parallelepipede oblique chacune des six faces estant un parallelogramme, et on le peut couper en le fendant en sorte que tous ces parallelogrammes soient des rombes egaux et semblables. La figure icy adjointe [Fig. 131, 131 bis] le represente de cette forme, et le rhombe qui fait la base est ACBI.

Il souffre d'estre fendu avec egale facilité dans toutes les trois dimensions par des coupes paralleles a quelqu'une de ses surfaces, et en separant ainsi les morceaux ils ont leur surfaces polies. Et il n'y a point d'autre moyen de les rendre telles, au moins tout ce que l'on a essayè jusqu'a present n'a point reussi⁴⁾.

3) Picard fit le voyage d'Uranibourg en 1671. Les cristaux d'Islande apportés par lui sont mentionnés dans la Correspondance le 8 juillet 1672 dans une lettre de Pardies (T. VII, p. 193). Le 4 septembre 1672 (T. VII, p. 219) Huygens écrit à son frère Lodewijk avoir fait des observations sur ces cristaux.

4) Huygens trouva en 1679 le moyen de polir une section plane quelconque; voyez la p. 442 qui suit.

[p. 410]

Les angles obtus des rhombes ou parallelogrammes qui font les surfaces sont de 101 degrè, et par consequent les angles de 79 degr. Des angles solides qui sont composez de 3 angles plans il y en a 2 opposez, comme dans la figure sont O et I, qui ont ces angles plans tous egaux, les autres 6 sont faits de 2 angles aigus et un obtus.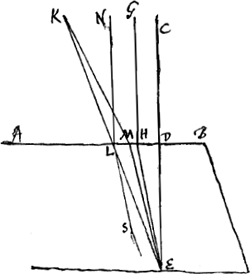

[Fig. 132.]

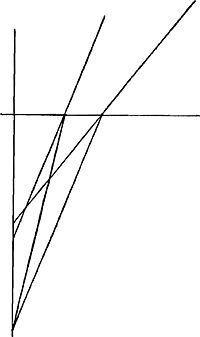
§ 3. AB [Fig. 132] quae angulum obtusum hedrae superioris bifariam dividit. CDE perpendicularis in AB representans sectionem seu latus superficiei planae erectae super hedram superiorem, simulque ad lineam AB.

GH alia superficies plana ipsi CD parallela, atque ita posita ut perpendicularis CH refringatur in HE ex refractione chrystalli anomala. Ita observatio docet radium quemcunque obliquum, in plano GH sumtum, refractionem habere in plano HE¹⁾.

Verum posito KLE radio illo obliquo qui lateribus parallelus est, is quidem irrefractus recta penetrat in LE²⁾. Sed alij in eodem plano KL¹⁾ sumti ac ad priorem KL obliqui non habent refractiones in plano LE, sed introrsum versus perpendicularem refringuntur ut in LS, idque tanto magis quanto erunt ad KL radium obliquiores.

Objectum E oculo in K posito apparet ex hac refractione in M.

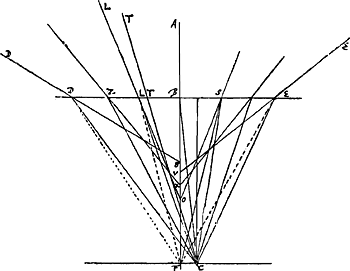
§ 4. Vide figuram subjectam [Fig. 133]. Linea DE quae angulum obtusum hedrae superioris bifariam dividit. Linea AB in planum ejus perpendicularis. BC refractio istius perpendicularis anomala. Angulus FBC refractionis radij perpendicularis est paulo minor 7 grad. cum ad solis radios inquiritur³⁾. TTC radius qui sine refractione

1) Comparez le § 5 qui suit. Le ‘plan HE’ est évidemment, comme les plans CDE et GH, perpendiculaire au papier, autrement dit perpendiculaire à la droite AB. Le ‘plan KL’ est également perpendiculaire au papier.

2) C'est ce que Bartholinus rapporte dans ses ‘Experimenta’ de 1669/1670. Plus tard Huygens reconnut que le rayon extraordinaire qui ne subit pas de réfraction n'est pas exactement parallèle aux arêtes. Il le constata ‘manifestement... le 3 Juillet 1679’ et joignit alors cette remarque à la présente Pièce; elle constitue la Partie A de la Pièce XI qui suit.

1) Comparez le § 5 qui suit. Le ‘plan HE’ est évidemment, comme les plans CDE et GH, perpendiculaire au papier, autrement dit perpendiculaire à la droite AB. Le ‘plan KL’ est également perpendiculaire au papier.

3) En 1677 Huygens prend 6^o50′ pour cet angle (p. 430 qui suit). Plus tard il adopte définitivement la valeur 6^o40′ qui est celle du Traité de la Lumière.

[p. 411]

[Fig. 133.]

transit, lateribus parallelus²⁾. BF crassitudo christalli. DS ad DF ut LO ad LF ut EV ad EF adeo ut si radij DD, LL, EE refracti irent ad F, esset refractio similis ordinariae, quae rationes sinuum sequitur. nisi quod cum ordinaria in hoc diaphano sit proximè ut 5 ad 3, haec est proximè minor quam 8 ad 5, quae itaque minor est ordinaria. Non feruntur autem radij refracti ad F sed ad C ubi nempe refractio BC radij perpendicularis AB fundum contingit⁴⁾.

Haec autem refractio anomala ejusmodi quidem est ad radios qui sunt in plano erecto super hedram secundum lineam DE⁵⁾ quae angulum hedrae obtusum bisecat, sed radiorum qui sunt in alijs planis super eandem quidem hedram erectis sed secundum alias lineas à DE primaria diversas, eorum tanto minor est refractio quanto magis ab hac linea planum incidentiae recedat, quod planum si secet rectam DE normaliter, fit refractio radiorum ejus plani quae 300 ad 217, hoc est proximè ea quae 11 ad 8. En marge: vel 10 ad 7⁶⁾.

2) C'est ce que Bartholinus rapporte dans ses ‘Experimenta’ de 1669/1670. Plus tard Huygens reconnut que le rayon extraordinaire qui ne subit pas de réfraction n'est pas exactement parallèle aux arêtes. Il le constata ‘manifestement... le 3 Juillet 1679’ et joignit alors cette remarque à la présente Pièce; elle constitue la Partie A de la Pièce XI qui suit.

4) Cette construction ne s'accorde pas tout à fait avec celle que Huygens déduisit plus tard de la considération des ondes sphéroïdales; voyez la Pièce VII qui suit et, à la p. 503, le par. 28 du Chap. V du Traité de la Lumière. D'après le § 2 de la Pièce VII (p. 429) il y a cependant à peu près un rapport constant dans le cas considéré entre le sinus de l'angle d'incidence et ce qui serait le sinus de l'angle de réfraction si, dans la Fig. 133, les ‘radij refracti irent ad F.’

5) Il s'agit toujours de la ‘hedra superior’, c.a.d. de la surface horizontale supérieure du cristal représentée par DE (Fig. 133) et perpendiculaire au papier.

6) La fraction 300/217 est comprise entre 11/8 et 10/7 et à peu près égale à 11/8.

[p. 412]

[Fig. 134.]

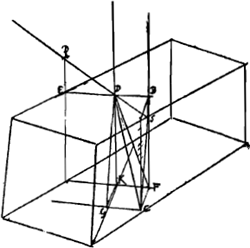
§ 5. Vide figuram pag. 5 hujus [Fig. 134]. Ut ad quemlibet incidentem radium habeatur planum quod refractio ejus sequi debet, imaginandum est primo planum per radium ductum atque ad superficiem erectum EDB. deinde ducenda recta DG quae foret refractio radij perpendiculariter ibidem incidentis. ac denique intelligendum planum DGCB per hanc rectam et per EDB eam quae radio incidenti in superficiem subjecta est sive quae est intersectio plani perpendicularis per radium cum superficie, eritque refractio in plano isto intra superficiem descendente.

Hinc intellexi ita se rem habere, ac si radius quilibet incidens [PD] regulari primum refractione feratur, sed non perveniat tamen ad punctum fundi quo ex hac refractione pervenire debebat (ut in figura hac est F) sed ad aliud punctum C, quod in linea ipsi DE subjecta¹⁾ accipiendum, cujusque distantiam ab F determinat angulus FBC sive KDG quo refractio perpendicularis anomala ab ipsa perpendiculari recedit. Et hoc in universum obtinet in quocunque plano ad superficiem fuerint radij incidentes.

Adeo ut motus radij refracti intra crystallum sit veluti compositus ex motu quem regulariter refractus haberet, et ex motu laterali cujus quantitas in toto descensu per crystallum est aequalis rectae FC²⁾.

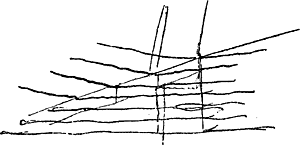
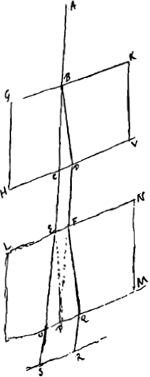
§ 7. AB [Fig. 135] radius solis. superficies GK tecta. foramen ad B. GK est quae bifariam dividit angulum obtusum hedrae superioris. Radius AB lateri GH parallelus. Refractio anomala radij AB transit recta usque in chartam EF. altera refractio ordinaria radij ejusdem fit in BD et inde rursus in DF, ipsi AB, eóque et ipsi CE parallelam.

1) Apparemment Huygens désigne ici par ‘linea ipsi DE subjecta’ la droite GC qui est une projection oblique (comparez le § 3, Fig. 132, qui précède) de DE sur la face inférieure du cristal. La figure fait voir que FC est parallèle à KG.

2) Cette construction - comparez la note 4 de la p. 411 - ne s'accorde pas avec celle que Huygens déduisit plus tard de la considération des ondes sphéroïdales (Traité de la Lumière, Chap. V, par. 38, p. 510 qui suit), dans laquelle subsiste cependant l'idée de la composition de deux mouvements (comparez la Partie C de la Pièce XI qui suit).

[p. 413]

[Fig. 135.]

[Fig. 135 bis.]

Quod si alterum crystalli frustum loco chartae EF objiciatur ut LNM, situ undequaque parallelo ipsi HGK (nec refert qua distantia a crystallo superiori absit) jam radius CE non dividetur rursus in duos ut AB, sed tantum recta trajiciet in chartam SR, nullam faciens ordinariam refractionem secundum EP. Neque item radius DF anomalam refractionem faciet secundum FP, sed tantum ordinariam secundum FQ et inde rursus secundum QR feretur ipsis DF et AB parallelus adeo ut duae tantum imagines lucidae foraminis B appareant in S et R.

Sed etiamsi radius AB à sole veniens perpendicularis incidat in superficiem GK vel alio quolibet angulo quam GHD inclinatus semper tantum duae imagines in SR cernuntur.

Item omni positu duorum frustorum quo alterutra diagonalis rhombi frusti superioris, ut in figura sequente [Fig. 135 bis] GK vel VT, parallela erit alterutri diagonali rhombi inferioris, duae duntaxat imagines transmittentur. Hae quoque in unum conveniunt in positione parallelae contraria, cum nempe L ponitur sub V et N sub H. En marge: inclinato tamen multum radio AB in superficiem GK pro duabus quatuor fiunt imagines his positionibus³⁾.

Quoties vero ab istis positionibus recedetur, quatuor imagines visentur, eaeque omnes aequaliter lucidae, cum aliquod latus hedrae superioris diagonio minori GK rhombi inferioris parallelum erit⁴⁾.

§ 8. Pour rendre raison du phenomene de la page precedente [§ 7], je me suis imaginè que dans ce crystal il y a deux matieres differentes, et qu'il y en a

3) Il y avait peut-être réflexion intérieure. Voyez la Pièce XII qui suit.

4) Il n'est donc pas exact, comme le dit Huygens dans le Traité de la Lumière, qu'il découvrit les phénomènes relatifs aux rayons qui passent successivement par deux cristaux d'Islande ‘après avoir écrit tout ce que dessus’ (p. 517 qui suit). En effet, la présente Pièce date de 1672 (ou 1673) et la rédaction du Traité ne fut entreprise qu'en 1678 après que Huygens eut découvert (en 1677; Pièce VII qui suit) l'explication par ondes sphéroïdales de la réfraction extraordinaire.

[p. 414]

pareillement deux differentes en l'air ou ether dont le mouvement fait ce que nous appellons lumiere. Et que les deux divers mouvements d'undulation¹⁾ de ces deux matieres de l'ether ont pouvoir d'emouvoir chacun sa matiere analogue des deux qui composent le crystal, et que reciproquement, ces matieres differentes du crystal estant esbranlees, ne scauroient imprimer ce mouvement de lumiere qu'a leur matiere analogue de l'ether.

Cela posè le premier rayon AB ayant dans soy les mouvements des deux matieres de l'ether, chacune de ces matieres esbransle celle qui luy est analogue dans le crystal, et cela fait les 2 rayons differents BC, BD; lesquels n'ayant chacun que le mouvement de l'une des matieres du crystal, il s'en suit qu'en sortant dans l'ether par CE, DF [Fig. 135] ils n'esbranlent chacun que l'une des matieres de l'ether qui leur sont analogues. d'ou vient que ces rayons CE, DF tombant en suite sur l'autre morceau de crystal, ils n'emeuvent chacun que leur matiere analogue, et partant ils ne se subdivisent plus dans le crystal, mais se rompent simplement en des rayons paralleles respectivement a ceux qui ont estè produits dans la piece de dessus par la division du rayon AB. Cependant il reste encore a dire pourquoy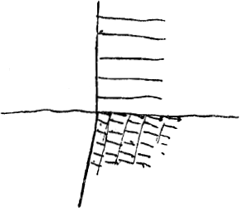

[Fig. 136.]

dans certaines positions de ces deux pièces de crystal l'une derriere l'autre, ces rayons DF, CE ne laissent pas de se partager encore chacun en deux, et font voir sur le papier SR quatre images du trou B, dont le carton GK est percè. Ce qui est tres difficile, car il faut pour cela, que ces rayons CE, DF quoyque non composez en frappant en certain sens la surface du crystal LN, puissent esbransler les 2 differentes matieres qui le composent, et en d'autres sens point.

§ 9. Comment le rayon perpendiculaire peut il devenir oblique par la refraction, car il arrivera que les ondes ne seront pas a angles droits a la ligne de leur extension ou emanation²⁾, contre ce que demande

1) Voyez sur les ‘mouvements d'undulation’ les p. 395-396, sur les différentes matières la p. 398 de l'Avertissement qui précède.

2) Comparez la Fig. 128 qui précède.

[p. 415]

notre hypothese de la lumiere. Est ce qu'il arrive en cecy comme si un rayon perpendiculaire tomboit sur une surface dentée en sorte qu'une partie d'onde se partage en plusieurs partielles plus petites [Fig. 136], qui s'avancent en suite chacune obliquement a la surface d'incidence, mais pourtant en ondes perpendiculaires a leur extension.