Logo DBNL
Die conste vanden getale (1999)

Die conste vanden getale

(1999)–Marjolein Kool–rechtenstatus Auteursrechtelijk beschermd

Een studie over Nederlandstalige rekenboeken uit de vijftiende en zestiende eeuw, met een glossarium van rekenkundige termen


Vorige Volgende

Hoofdstuk 6
Relaties tussen de rekenboeken

De auteurs van de rekenboeken behandelen vrijwel allemaal hetzelfde onderwerp: het rekenen met Hindoe-Arabische cijfers.1 De één vult dit onderwerp aan met algebra, de ander met penningrekenen, een derde voegt nog wat extra vraagstukken toe, maar het hoofdthema staat vast. De auteurs leggen uit hoe men moet rekenen met gehele getallen en breuken en hoe die rekenkundige kennis kan worden toegepast bij het oplossen van praktische vraagstukken.

De rekenboeken vertonen onderling zoveel overeenkomsten dat men zich kan afvragen in welke mate de auteurs bij het schrijven van hun rekenboek gebruik hebben gemaakt van het werk van hun voorgangers. Wie gebruikte wie en op welke wijze?

Om deze vraag te kunnen beantwoorden, zijn alle rekenboeken uit het corpus systematisch met elkaar vergeleken. Waar een relatie werd ontdekt, is deze beschreven. Er zijn ook enkele relaties met niet-Nederlandstalige rekenboeken gevonden en beschreven. Nader onderzoek levert wellicht nog meer anderstalige bronnen op, of - omgekeerd - anderstalige werken die gebaseerd zijn op Nederlandse rekenboeken.

De gevonden relaties vormen met elkaar een tamelijk complex netwerk. Enkele relaties uit dit netwerk zijn al eerder beschreven. Bockstaele onderzocht het bronnengebruik van Gielis van den Hoecke en de relaties tussen de verschillende drukken van Die maniere....2 Smeur vermeldt de mogelijke bronnen van een aantal gedrukte Nederlandse rekenboeken.3 In het hierna volgende hoofdstuk wordt voor het eerst geprobeerd een totaaloverzicht te geven van het bronnengebruik en de andersoortige relaties tussen alle tot nu toe bekende Nederlandstalige rekenboeken uit de vijftiende en zestiende eeuw. De opvallend grote samenhang tussen de rekenboeken werpt nieuw licht op de werkwijze van de auteurs.

 

Om de beschrijving van het netwerk overzichtelijk te houden, is dit opgedeeld in vijf stukken. Die vijf stukken worden in de eerste vijf paragrafen van dit hoofdstuk beschreven. In elke paragraaf staat één rekenboek centraal, dat is het reken-

boek dat opvallend veel relaties heeft met andere rekenboeken. Deze vijf rekenboeken vormen als het ware belangrijke knooppunten in het netwerk.

 

De vijf centrale rekenboeken zijn:

1.D-Man-1508
2.D-Hoe-1537
3.De werken van Valentin Mennher, 1550-15734
4.H-BKB-1568
5.D-Dij-1591

Aan het eind van dit hoofdstuk worden de vijf stukken van het netwerk samengevoegd tot een geheel.

De schematische weergave van het netwerk moet als volgt gelezen worden. De rekenboeken in een dubbelomlijnd kader zijn Nederlandstalig. De cursief gedrukte namen in de enkele kaders verwijzen naar niet-Nederlandstalig werk. Een stippellijn tussen twee rekenboeken betekent dat er een verband tussen beide werken bestaat, maar dat niets zeker is over de aard van dat verband. Alle overige lijnen in het netwerk geven aan dat het oudste rekenboek mogelijk een bron is geweest van het jongere. Uiteraard moet hierbij niet de mogelijkheid uitgesloten worden dat niet dit rekenboek, maar een werk dat verloren is gegaan de werkelijke bron is geweest.

De wijze waarop een mogelijke bron door een latere auteur gebruikt is, kan heel verschillend zijn. Er kan sprake zijn van woordelijk afschrijven van omvangrijke tekstgedeelten; dat wordt in het schema weergegeven met een doorgetrokken lijn. De auteur kan zijn bron ook bewerkt hebben; dat houdt in dat hij de teksten die hij aan zijn bron ontleent nu eens woordelijk overneemt, dan weer herformuleert, samenvat, voorziet van commentaar, enz. Soms worden teksten uit verschillende bronnen gecompileerd. Als een auteur zijn bron bewerkt heeft, is dat aangeduid met bolletjes op de doorgetrokken lijn. Bij een buitenlandse bron is er meestal sprake van vertaling. Dit is aangegeven door middel van een verbindingslijn met dwarsstreepjes.

De mate van ontlening kan sterk variëren. In D-Guc-1569 komen bijvoorbeeld slechts vier vraagstukken voor die vermoedelijk uit D-Man-1510 afkomstig zijn, terwijl H-GrU-1558 in zijn geheel een afschrift is van D-Hoe-1537. Een extra dikke doorgetrokken lijn geeft aan dat er van een aanzienlijke ontlening sprake is.

Elke lijn in het netwerk draagt een nummer. Dat nummer correspondeert met de paragraaf waarin de relatie tussen de twee met elkaar verbonden rekenboeken wordt beschreven. Rekenboeken die niet met andere werken in verband gebracht kunnen worden, zijn niet in het schema opgenomen. Ze worden in de zesde paragraaf beschreven.

Vooraf kan niet nadrukkelijk genoeg gesteld worden dat het in dit hoofdstuk

gaat om hypotheses, om vermoede relaties tussen overgeleverde werken. Rekenboeken zijn nu eenmaal een gebruiksartikel en in de loop der eeuwen zijn er ongetwijfeld vele verloren gegaan. Het is onmogelijk om met zekerheid directe afhankelijkheid tussen rekenboeken vast te stellen. De mogelijkheid van een verloren gegane tussentrap of een gemeenschappelijke, niet overgeleverde bron, is immers niet uit te sluiten.

6.1 D-Man-1508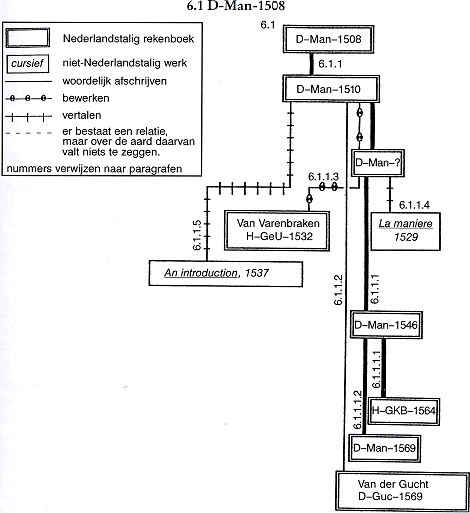



illustratie
Figuur 6.1. Het netwerk van relaties rond D-Man-1508.


Het oudste gedrukte rekenboekje in de Nederlandse taal is ‘Die maniere om te leeren cyffren na die rechte consten Algorismi. Int gheheele ende int ghebroken’. Dit werkje werd in 1508 voor het eerst gedrukt. De auteur is onbekend. Het be-

handelt het rekenen met Hindoe-Arabische cijfers, enkele rekenregels en vraagstukken. Het penningrekenen ontbreekt.

6.1.1 D-Man-1510

D-Man-1508 werd in 1510 herdrukt, uitgebreid met een gedeelte over penningrekenen.

6.1.1.1 D-Man-1546

In 1546 werd Die maniere... nogmaals gedrukt. Dit boekje zou een herdruk van de uitgave van 1510 kunnen zijn, maar er zijn enkele verschillen. In D-Man-1546 komt in het hoofdstuk over numeratie een tabel voor die in D-Man-1510 ontbreekt. Ook de tafels van vermenigvuldiging die in D-Man-1546 zijn opgenomen, komen in D-Man-1510 niet voor. In paragraaf 6.1.1.4 wordt de mogelijkheid besproken van een verloren gegane onbekende herdruk van D-Man-1510 die voor 1529 verschenen zou zijn. Misschien gaat D-Man-1546 op deze onbekende herdruk terug.

6.1.1.1.1 H-GKB-1564

In H-GKB-1564 wordt uitsluitend het penningrekenen behandeld. Het tractaat vertoont grote overeenkomsten met zowel het gedeelte over penningrekenen uit D-Man-1510 als dat uit D-Man-1546. De overeenkomsten zijn zo nauw dat moeilijk vast te stellen is met welke van de twee drukken de verwantschap het grootst is.

Eén optelling werpt wat licht op deze zaak. In H-GKB-1564 staat:

Men es u schuldich 10 ponden,
18 ponden, 100 ponden, 50
ponden, 69 ponden.5

De vraag is hoeveel schuld dit gezamenlijk is. In beide gedrukte boeken komt een vergelijkbare optelling voor.

In D-Man-1510 wordt opgeteld: 20, 8, 50 en 69.

In D-Man-1546 wordt opgeteld: 20, 8, 100, 50 en 69.

De optelling in H-GKB-1564 vertoont meer overeenkomsten met die in D-Man-1546 dan met die in D-Man-1510, in die zin dat de som van de optelling dezelfde is. De scribent van H-GKB-1564 heeft mogelijk D-Man-1546 als bron gebruikt en bij het overnemen van het eerste getal een schrijffout gemaakt die hij bij het tweede getal zonder knoeien heeft gecorrigeerd. Overigens is het niet uit te sluiten dat de scribent van H-GKB-1564 niet D-Man-1546, maar de verloren gegane onbekende herdruk van Die maniere... heeft afgeschreven die in 6.1.1.4 besproken wordt.

Over de persoon van de scribent is niets bekend, maar opvallend is dat zijn taalgebruik sporen van een Oost-Nederlands dialect draagt. In zijn woordenschat komen termen voor als: dividiren, yerste, averbliven, averlopen, vermenichfoldighen.6

6.1.1.1.2 D-Man-1569

In 1569 is Die maniere... nogmaals herdrukt. Deze herdruk vertoont meer overeenkomsten met de druk uit 1546 dan met die uit 1510. Dat blijkt bijvoorbeeld uit de optelling met penningen die hiervoor al ter sprake kwam. Zowel in D-Man-1569 als in D-Man-1546 worden 20, 8, 100, 50 en 69 ponden opgeteld. Bovendien worden in de laatste twee rekenboeken controles uitgevoerd met de negenproef en niet met de zevenproef zoals in D-Man-1510 het geval is.

6.1.1.2 D-Guc-1569

Van der Gucht behandelt in zijn rekenboek vier vraagstukken die woordelijk overeenkomen met vraagstukken uit Die maniere....7 De vraag is welke editie van Die maniere... Van der Gucht hiervoor gebruikt heeft. Die vier vraagstukken zijn namelijk vrijwel identiek in D-Man-1510 en D-Man-1546 opgenomen. Uit het vergelijken van de overeenkomstige passages blijkt, dat D-Guc-1569 op twee plaatsen een sterkere overeenkomst met D-Man-1510 vertoont dan met D-Man-1546. In D-Guc-1569 staat:

Een haze loopende int velt,
overloopt in eender minute+
(waer af datter 60 in 1+
huere commen), 12 roeden+
lands.8

Dit komt woordelijk overeen met de tekst in D-Man-1510. In D-Man-1546 ontbreken de haakjes.

Een tweede sterkere overeenkomst tussen D-Guc-1569 en D-Man-1510 bevindt zich in het vraagstuk van de twee gezellen die elkaar tegemoet reizen. Het eindigt als volgt:

Zy gaen 4 daghen ende 4/14 van
eenen daghe eer zy+
vergaderen.+9

Dit komt zo ook in D-Man-1510 voor. In D-Man-1546 staat het laatste woord in de verleden tijd, namelijk vergaderden. Dit doet vermoeden dat Van der Gucht zijn vier vraagstukken mogelijk uit D-Man-1510 heeft overgenomen en niet uit D-Man-1546.10 Daarnaast heeft hij nog van andere bronnen gebruik gemaakt.11

6.1.1.3 H-GeU-1532

H-GeU-1532, het rekenboek van Van Varenbraken, vertoont grote overeenkomsten met D-Man-1510.12 De proloog en grote fragmenten uit het penningrekenen

komen woordelijk overeen met de tekst van D-Man-1510. In H-GeU-1532 is zelfs een fout uit D-Man-1510 overgenomen. Dat gebeurt in de uitleg van het lenen bij aftrekken:

Maer zijnt oneffen ghetalen+
oft dat die onderste somme+
in haer beginsel meerder+
waer dan de opperste somme,
so moet ghi altijt 1+
ontleenen aen die naeste+
letter oft cijffer.+13

Dit komt woordelijk overeen met de tekst in H-GeU-1532 (fol. 134r) terwijl het begin van deze opmerking Maer zijnt oneffen ghetalen helemaal niets met lenen te maken heeft.

Ook komen in beide rekenboeken 69 overeenkomstige vraagstukken voor. Dat wil zeggen dat deze vraagstukken qua context, rekenkundige inhoud en oploswijze identiek zijn, maar dat er soms wel verschillen in de formuleringen zijn. Zie bijvoorbeeld het volgende vraagstuk uit D-Man-1510:

Drie ghesellen hebben te
samen een scip ghecocht voer
60 ponden grote, waer af de+
eerste betaelen moet ½, die
tweede ⅓ ende die derde ¼.
Nu is die vraghe, hoe vele
dat elck juyst betalen sal+
voer zijn deel. Wildij dese+
ende deser ghelike questien
solveren, so neemt voer+
den eerste ½ van 60, dat is
30. Voer den tweeden ⅓ van 60,
dat is 20. Ende den derden ¼,
dat is 15. Nu addeert dese
drie sommen te gader, coemt+
65.14

In het rekenboek van Christianus van Varenbraken wordt ditzelfde vraagstuk als volgt verwoord:

Drie ghesellen hebben een
scip ghecocht voor 60 ponden
grote, waer af deerste
betalen moet die ½, die
ander het ⅓ ende die derde+
het ¼. Die vraghe es, hoe
veel elc juuste sal moeten+
geven voor sijn deel. Nu soo
besiet welc die ½ es van 60
ende compt 30. Ende welc het
derdendeel es van 60 ende
compt 20. Ende welc het ¼ es
van 60 ende compt 15.
Sommeirt dit altesamen ende+
sal comen 65.15

Het zou kunnen zijn dat Van Varenbraken hier tamelijk vrij met de tekst in D-Man-1510 is omgesprongen, zelf breukstrepen heeft toegevoegd en zinnen anders heeft geformuleerd. Maar op andere plaatsen zijn er nog meer verschillen tussen D-Man-1510 en H-GeU-1532. In tegenstelling tot de auteur van D-Man-1510 controleert Van Varenbraken zijn berekeningen met de negenproef in plaats van met de zevenproef.16 Hij behandelt bij het penningrekenen ook de bewerkingen halveren en verdubbelen, terwijl die in D-Man-1510 niet voorkomen. Hij stelt het rekenen met gehele getallen en breuken gelijktijdig aan de orde, terwijl dit in D-Man-1510 in twee afzonderlijke hoofdstukken gebeurt.

Er bestaat wel degelijk een relatie tussen D-Man-1510 en H-GeU-1532. Het is alleen niet duidelijk of Van Varenbraken rechtstreeks of indirect uit D-Man-1510 geput heeft. Misschien wordt er ooit nog een onbekende herdruk of een onbekend afschrift van Die maniere... gevonden, waarmee nieuw licht op de zaak wordt geworpen. Het vermoeden dat er zo'n onbekende versie heeft bestaan, zal in de volgende paragraaf (6.1.1.4) onderbouwd worden.

In ieder geval is Die maniere... niet de enige bron geweest van H-GeU-1532. Van Varenbraken behandelt 82 vraagstukken die niet in Die maniere... voorkomen en die waarschijnlijk uit een of meer andere bronnen afkomstig zijn.

6.1.1.4 La maniere...

Die maniere... is ook een bron geweest voor rekenboeken die niet in de Nederlandse taal geschreven zijn. In 1529 verscheen te Antwerpen La maniere pour aprendre a cyfrer et compter par plumes et gectz selon la vraie science de algorisme en nombre entier et rompu. Het is een vertaling van Die maniere.... Bockstaele ontdekte dat het Franse rekenboek de grootste overeenkomsten vertoont met de uitgaven van Die maniere... uit 1546 en 1569. In alledrie de rekenboeken worden controles met de negenproef uitgevoerd, terwijl in D-Man-1510 gecontroleerd

wordt met de zevenproef. Dat doet vermoeden dat er voor 1529 nog een onbekende herdruk van het oudste Nederlandse rekenboekje geweest.

Natuurlijk is het mogelijk dat de auteur van La maniere... zelf op het idee is gekomen om de zevenproef in zijn bron door de negenproef te vervangen. Bockstaele toont aan dat dat waarschijnlijk niet het geval is geweest.17 De passage over de negenproef in het Franse rekenboek bevat de ongebruikelijke Franse uitdrukking compter dehors. Dat moet haast wel een vertaling zijn van het Nederlandse uittellen. Als er werkelijk zoals hiervoor verondersteld wordt, voor 1529 een onbekende herdruk van D-Man-1510 is gepubliceerd, zou dat eventueel ook de bron geweest kunnen zijn van H-GKB-1564, D-Man-1569 (in plaats van D-Man-1546) en H-GeU-1532.

6.1.1.5 An introduction...

De anonieme auteur van het oudste gedrukte Engelse rekenboekje An introduction for to lerne to recken with the pen, or with counters accordynge to the trewe cast of algorysme, in hole nombers or in broken..., gedrukt in 1537, heeft in zijn rekenboek D-Man-1510 vrijwel geheel vertaald, aangevuld met fragmenten uit een Frans rekenboek.

 

Samenvattend kan worden vastgesteld dat het eerste gedrukte rekenboekje in de Nederlandse taal de basis is geweest voor verschillende latere rekenboeken in binnen- en buitenland. Waarschijnlijk hebben er zelfs nog wel meer drukken en afschriften van Die maniere... bestaan dan de versies die nu bewaard zijn gebleven. Die maniere... was zowel in de Nederlanden als in Engeland en Frankrijk vermoedelijk een van de weinige gedrukte rekenboeken in de volkstaal waar men aan het begin van de zestiende eeuw over kon beschikken.

6.2 D-Hoe-1537

Naast Die maniere... is D-Hoe-1537 het enige andere Nederlandstalige rekenboek dat voor zover bekend in de eerste helft van de zestiende eeuw is gedrukt. Van den Hoecke, de auteur van dit rekenboek, is een van de weinigen die expliciet aangeeft dat hij bronnen gebruikt heeft. Die bronnen zijn blijkbaar uit verschillende taalgebieden afkomstig, want in de proloog staat:

In dese boec wert ghestelt
tbeste uut van veel diveersche
boecken, als uut Latijnsche,+
Overlantsce, Ytaliaensce ende+
Walsce boecken.+18

Welke bronnen dit zouden kunnen zijn, wordt hierna beschreven.



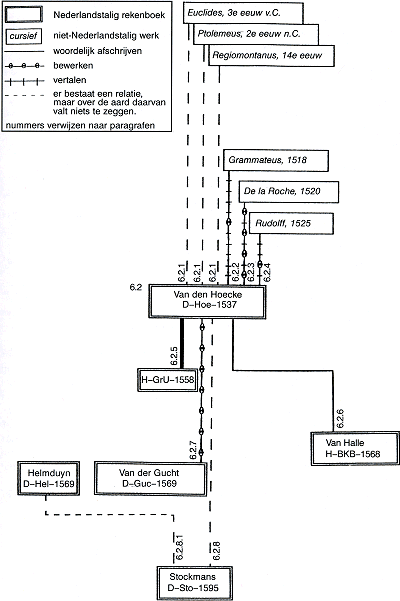illustratie
Figuur 6.2. Het netwerk van relaties rond D-Hoe-1537.


6.2.1 Euclides, Ptolemeus en Regiomontanus

Slechts een enkele keer noteert Van den Hoecke de namen van de auteurs van zijn bronnen. In zijn hoofdstuk geometria in cos behandelt hij de stelling van Pythagoras. Hij kondigt dit onderwerp als volgt aan:

Nu na dye leeringe van Euclides+
inden eersten boec int 47
capittel.19

Hier verwijst Van den Hoecke naar De Elementen van Euclides (3e eeuw v.C.).20 In zijn hoofdstuk over verhoudingen noemt hij bij zijn berekeningen van dye cirkels des hemels:

Nu na de leeringhe van+
Ptholomeus, dictione prima,+
capi.13.21

Dit verwijst naar de Almagest van Ptolemeus (2e eeuw n.C). Een paar regels verder schrijft Van den Hoecke:

Nu na dye leeringhe van Johannes+
de Monte Regio.22

Welk werk van Regiomontanus hier bedoeld wordt, is onduidelijk.

Het is niet bekend welke edities van de werken van Euclides, Ptolemeus en Regiomontanus door Van den Hoecke gebruikt zijn en of hij inderdaad wel rechtstreeks uit hun werken geput heeft. Het is goed mogelijk dat deze beroemde auteurs geciteerd worden via werk van anderen. In dat geval zijn het geen rechtstreekse bronnen van D-Hoe-1537 geweest. Een vergelijkbare situatie doet zich bijvoorbeeld voor in H-BKB-1568. Op fol. 161r vermeldt Van Halle, de auteur van H-BKB-1568, bij een berekening met de stelling van Pythagoras dat deze afkomstig is uit het eerste boek van Euclides. Het blijkt dat hij deze opmerking woordelijk vertaald heeft uit zijn bron, het rekenboek van Gemma Frisius.23 Van Halle hoeft de Elementen van Euclides niet zelf ingezien te hebben. Ook bij Van den Hoecke kan dit het geval zijn. In zijn korte passages over meetkunde en astronomie noemt hij wél namen van auteurs en in de rest van het rekenboek niet. Deze namen zijn mogelijk afkomstig uit een onbekende bron, waaruit hij deze passages heeft overgenomen zonder dat hij zelf het werk van de beroemde auteurs heeft ingezien.

Bockstaele heeft nader onderzoek gedaan naar de bronnen die Van den Hoecke mogelijk in de rest van zijn werk gebruikt heeft.24 Hij vond er drie:

6.2.2 Grammateus

Van den Hoecke heeft een aantal fragmenten uit het rekenboek van Henricus Grammateus woordelijk vertaald.25 Het gaat om tekstgedeelten over numeratie, optellen, aftrekken en penningrekenen. Bij de behandeling van gewichten, maten en tijd voegt hij verschillende gegevens uit andere steden toe en bij het breukenrekenen noteert hij enkele vraagstukken die niet bij Grammateus voorkomen. De symbolen die Van den Hoecke gebruikt voor de notatie van machten van de onbekende zijn tamelijk ongebruikelijk. Ze komen overeen met die van Grammateus.26

6.2.3 De la Roche

De inleiding die Van den Hoecke geeft op de regel van drieën is waarschijnlijk geïnspireerd door de inleiding uit het werk van Estienne de la Roche.27 De la Roche schrijft:

La regle de troys est la
premiere, la plus utile et la
plus belle de toutes les regles
darismetiqtie ... Et pour ce
selon aulcuns philosophes a este
appellee ‘regle doree’. Et selon
daultres ‘regle de proportions
des nombres’.28

Van den Hoecke:

Die reghel van dryen is die
excellenste ende schoonste+
regule van alle ander regulen.
Dewelcke sommighe philosophen
hebben gheheeten ‘de gulden
regule’ ende ander hebbense
ghenaemt ‘die regule vander
proporcien’.29

In het hoofdstuk over wortels en wortelvormen maakt Van den Hoecke veel gebruik van het werk van De la Roche. Het stuk over de reductie en abbreviatie van wortels en over het trekken van tweede- en derdemachtswortels is een verkorte versie van wat De la Roche schrijft. Verschillende passages zijn woordelijk vertaald en een aantal getallenvoorbeelden zijn onveranderd overgenomen. Van den Hoeckes notatie van wortelvormen - met de symbolen R, R3, R4, ... -, komt overeen met die van De la Roche.30

6.2.4 Rudolff

Voor het onderricht in het rekenen met wortelvormen heeft Van den Hoecke gedeelten uit het werk van Christoff Rudolff vertaald,31 maar hij heeft de worteltekens door die van De la Roche vervangen. Ook het gedeelte Van die proporcien is uit de algebra van Rudolff afkomstig. Ten slotte is ook het hoofdstuk over algebra en het oplossen van vergelijkingen grotendeels aan deze bron ontleend. Maar Van den Hoecke gebruikt de symbolen uit het werk van Grammateus (zie paragraaf 6.2.2). Bovendien voegt hij verschillende voorbeelden toe.

Het is onmogelijk een volledig beeld te geven van de bronnen die Van den Hoecke gebruikt heeft voor de enorme verzameling vraagstukken in zijn rekenboek. Naast de werken van Grammateus, Rudolff en De la Roche vermoedt Bockstaele onder andere ook Italiaanse bronnen.

6.2.5 H-GrU-1558

Op zijn beurt werd het rekenboek van Van den Hoecke weer gebruikt door latere auteurs. De folia 1r tot en met 123r zijn woordelijk afgeschreven door de scribent van H-GrU-1558, inclusief de rekenfouten. Blijkbaar had hij niet de beschikking over de lijst van errata, die Van den Hoecke aan het eind van zijn rekenboek heeft toevoegd. Slechts twee keer voegt de scribent iets toe aan zijn bron. Dat is op fol. 48v de tekst: ANNO 1558 en boven de tafels van vermenigvuldiging het opschrift: Tafel pyetagoras. De folia 9r, 9v, 123v t/m 176v heeft hij om onbekende redenen niet afgeschreven.32

6.2.6 H-BKB-1568

Van Halle, de auteur van H-BKB-1568, heeft gebruik gemaakt van het rekenboek van Van den Hoecke. Bij zijn uitleg van de regula falsi vermeldt hij expliciet de naam van zijn bron:

Dus leert Gielis Hoecte in+
sijn arithmetica.33

Van Halles hoofdstuk over algebra, waarin het rekenen met algebraïsche vormen wordt geleerd, komt woordelijk overeen met de tekst van Van den Hoecke, inclusief diens ongebruikelijke notatiesysteem. Van Halle heeft het algebraïsch oplossen van vergelijkingen niet uit zijn bron overgenomen. Dit onderwerp komt in H-BKB-1568 niet voor.34

6.2.7 D-Guc-1569

Ook in D-Guc-1569 zijn enkele gedeelten aan D-Hoe-1537 ontleend. Het gaat om twee grotere stukken: de uitleg van de regula falsi35 en de uitleg van de regel van voyage, waarin ook wat astronomie voorkomt, wat in de rekenboeken een ta-

melijk ongebruikelijk onderwerp is.36 Naast deze fragmenten bevatten beide rekenboeken nog enkele kleinere overeenkomstige passages.

Van der Gucht springt vrij met zijn bron om. Hij neemt bepaalde passages woordelijk over, maar op andere plaatsen wijzigt hij de tekst of geeft hij aanvullingen, meestal ter verduidelijking. Beide auteurs behandelen bijvoorbeeld een handige manier om het product van 2100 × 34000 te berekenen. Van den Hoecke schrijft:

Om te multipliceren sommen+
daer veel cyfers voor staen,+
als wildi multipliceren 2100
met 34000, so multipliceert
21 met 34, coemt 714. Daer+
toe stelt also vele cyfers
vooren als aen beyde
de sommen staen. Dat sijn+
00000, coemt 71400000. Doet
desghelijcx van ander.+37

Van der Gucht schrijft:

Om te multipliceren sommen+
daer veel cijfers, ghezeyt+
‘nullo’ vooren staet, als+
wilt ghij multipliceren 2100
met 34000, zo multipliceert
21 met 34, comt 714. Daer toe
stelt also veel cijferen
vooren an de rechterhand vande
somme als an beede de
voorzeyde sommen staen. Dat+
zijn 00000, comt 71400000.
Doet des-ghelijcken van
anderen daer veel nullus oft
0 vooren staen. Waer af hier+
noch zommighe exempelen+
volghen.38

Van der Gucht behandelt meer voorbeelden en heeft meer oefenmateriaal dan Van den Hoecke. Waarschijnlijk richt hij zich tot een eenvoudiger publiek dan zijn collega. Dat blijkt bijvoorbeeld ook uit het feit dat hij bepaalde ‘moeilijkere’ onderwerpen uit het werk van Van den Hoecke niet overneemt: rekenen met wortelvormen, algebra, verhoudingen en het berekenen van de middelevenredige. Leerlingen die zich nader in de rekenkunde willen verdiepen, verwijst hij naar zijn bron. Aan het eind van zijn uitleg over worteltrekken schrijft Van der Gucht:

Angaende van noch breeder+
bescheet vande radix, als van+
tquadraet ende cubijck ofte in+
numerus surdus, in rationale+
ende irrationale, in+
communicanten, binomium etc.,+
oock vande proportien ende+
de reghele cos met alle haer+
specien, dit salmen al vijnden+
bij meester Gillis vanden
Houcke die daer af int langhe
tracteert.+39

Net als Van Halle noemt Van der Gucht hier expliciet de naam van de auteur van zijn bron. Dit is niet gebruikelijk.

 

Naast D-Hoe-1537, gebruikte Van der Gucht nog verschillende andere bronnen. Al eerder is vermeld dat hij vier vraagstukken vermoedelijk uit D-Man-1510 overnam.40 Aan het begin van zijn rekenboek, in de Franse opdracht aan de kooplieden van Brugge, noemt hij zijn rekenboek extraict et composé en partie de plusieurs livres et autheurs. Welke bronnen hij hier bedoelt naast D-Man-1510 en D-Hoe-1537 is niet duidelijk. Het Franse rijmpje op fol. 58v doet vermoeden dat hij minstens een Frans rekenboek heeft geraadpleegd. Als hij heeft uitgelegd hoe het rekenwerk bij de regel van drieën moet worden uitgevoerd, voegt hij daaraan toe:

Waer op den Francoys stelt+
een verzeken aldus:+
Multiplie le second par le tiers.
Et divisé le nombre provenu
par le premier.
Tant es rompu que entiers,
le quotient est le quart incognu.41

6.2.8 D-Sto-1595

D-Sto-1595, het rekenboek van Stockmans, bevat enkele passages die zowel in D-Guc-1569 als in D-Hoe-1537 voorkomen. In paragraaf 6.2.7 is beschreven dat de auteur van D-Guc-1569 het rekenboek van D-Hoe-1537 als bron gebruikt heeft. Het is moeilijk vast te stellen of Stockmans rechtstreeks uit D-Hoe-1537 heeft geput of indirect via D-Guc-1569. Uit de volgende overeenkomstige passages is dat bijvoorbeeld niet op te maken:

D-Hoe-1537:

Vint mi een ghetal dat ic
multiplicere met 14 ende den+
quocient dividere doer 4⅔ dat+
come 18.+42

D-Guc-1569:

Vint my een ghetal dat ick
multiplicere met 14 ende den
quocient dividere duer 4⅔ dat
comme 18.43

D-Sto-1595:

Soeckt eenich ghetal dwelc met+
14 gemultipliceert wesende,+
tproduct met 4⅔ gedivideert,+
den facit oft quotient 18 sy.+44

D-Hoe-1537:

Twee lieden willen een stede
omme gaen wiens circunferencie+
is 3 mijlen. Ende scheydende
ghelijc van eender plaetse,+
den eenen gaet op een ure ⅘+
van eender mijlen, ende die
ander gaet ⅔ van eender mijle
op een ure.45

D-Guc-1569:

Twee lieden willen een stede
omme gaen wiens circunferentie
is drie mijlen. Ende scheedende
ghelijck van eender plaetse,
den eenen gaet op een huere ⅘+
van eender mijlen, ende die
ander gaet ⅔ van een mijle up
een huere.46

D-Sto-1595:

Twee gesellen willen een
plaetse ommegaen wiens
circonfirentie oft ommeganc+
is 3 mijlen. Ende sy scheyden
van malcanderen op een plaetse
wesende, gaende deen na der
rechter hant ende den anderen
na de slincke bant om. Ende+
den eenen gaet in een ure ⅘
van eende mylen, den anderen
⅔ van eender mylen.47

De verschillen tussen de fragmenten van Stockmans en die van de andere twee auteurs zijn zo groot, dat op basis van deze voorbeelden niet is vast te stellen of Stockmans gebruikt heeft gemaakt van D-Hoe-1537 of van D-Guc-1569. De definitie van vermenigvuldigen geeft uitsluitsel.

 

D-Hoe-1537:

Multitiplicatie is deen ghetal+
vermenighen met een ander+
ghetal. Dat is also veel als+
den multiplicateur of
multitipliceerder in hem selven+
bevangt, so menich werf te+
augmenteren oft+
menichfuldighen den nommer
den welcken ghemultipliceert
moet werden.48

D-Guc-1569:

Hier naer volcht de zeste
specie, ghenaemt multiplicatie.+
De welcke es een ghetal of
somme te multiplieren ofte+
vermenighen bij een ander.+
Dats deen somme zoo veel
meerder ende grooter te
maken als de ander somme+
bedraeght daer duer ghijse+
multiplieert.+49

D-Sto-1595:

De multiplicatie die leert het+
een ghetal door een ander te
vermeerderen. Dat is zoo veel+
als den multiplicateur oft den
multipliceerder in hemzelven+
besluyt ende bevanct, zoo+
menichmaels te multipliceren,+
te vermeerderen oft te
augmenteren den nommer oft+
t'ghetal dwelcmen begheert te
multipliceren.50

Van der Gucht heeft voor dit onderwerp geen gebruik gemaakt van D-Hoe-1537. Het fragment van Stockmans vertoont geen overeenkomsten met D-Guc-1569, maar wél met dat in D-Hoe-1537. Het frappantst is het gebruik van het woord multipliceerder, dat buiten deze twee rekenboeken nergens is aangetroffen. Er bestaat dus een relatie tussen D-Sto-1595 en D-Hoe-1537 en waarschijnlijk niet tussen D-Sto-1595 en D-Guc-1569. De aard van die relatie is niet duidelijk. Het gaat om slechts enkele overeenkomstige passages en zoals hiervoor is gebleken, is er geen woordelijke overeenkomst. Die verschillen in formulering zouden bijvoorbeeld ontstaan kunnen zijn doordat Van den Hoecke en Stockmans beide dezelfde (buitenlandse) bron hebben gebruikt of doordat Stockmans gebruik heeft gemaakt van een herdruk of afschrift van het rekenboek van Van den Hoecke. Nader speurwerk, ook naar buitenlandse bronnen, zou meer duidelijkheid in deze kwestie kunnen brengen.

6.2.8.1. D-Hel-1569

In hoofdstuk 7 wordt uiteengezet dat het enorme aantal synoniemen in D-Sto-1595 erop wijst dat de auteur vermoedelijk van verscheidene bronnen gebruik heeft gemaakt.51 Over het bronnengebruik van Stockmans bestaan echter nogal wat vragen. Hiervoor is vastgesteld dat er een relatie bestaat tussen D-Hoe-1537 en D-Sto-1595, maar dat de aard van die relatie onduidelijk is. Hetzelfde kan gezegd worden van het verband tussen D-Sto-1595 en D-Hel-1569.52

Beide rekenboeken bevatten een aantal overeenkomstige passages, onder andere bij de regel van drieën voor gehele getallen53, de regel van drieën voor breuken54, de regel van gezelschap55, de regel van gezelschap met tijd56 en de regula falsi.57 Er zijn overeenkomsten in de uitleg en er zijn enkele overeenkomstige vraagstukken. Maar ook hier geldt weer dat de overeenkomsten vooral inhoudelijk zijn en dat er verschillend geformuleerd wordt:

Helmduyn schrijft:

Soomen telt 4 realen voor een+
worp tot 3½ stuyvers t'stuck,+
wat sullen beloopen de 124+
worpen?58

terwijl Stockmans schrijft:

Als 4 realen van 3½ stuyvers
tstuc worden voor eenen worp
ghereeckent, vraghe wat de+
124 realen doen zullen.+59

Het doet vermoeden dat beide auteurs een gemeenschappelijke (buitenlandse) bron hebben gebruikt. Welke bron dat zou kunnen zijn is niet bekend.

Mocht er zo'n buitenlandse bron gevonden worden, dan zal blijken dat in ieder geval een van beide auteurs er tamelijk vrij mee omspringt. Zo is er bijvoorbeeld een vraagstuk dat in beide rekenboeken voorkomt, maar met verschillende getallen. Helmduyn schrijft:

Als op een solder, lanck+
zijnde 48 ende breet 20
voeten, leggen mach 24 lasten+
garst, vraghe: Wat machmen op+
een solder legghen die lanck
is 36 ende breet 14 voeten?60

Stockmans schrijft:

Alsmen op een solder, lanc
wesende 53 voeten ende breet
28 voeten, mach legghen 45
lasten, hoeveel zalmender
legghen op eenen solder,
lanck wesende 38 voeten ende
breet 19 voeten?61

Voorlopig levert dit alles slechts de conclusie op dat er een of ander verband bestaat tussen D-Hel-1569 en D-Sto-1595.

 

Samenvattend kan van D-Hoe-1537 worden vastgesteld, dat het werk waarschijnlijk bij de totstandkoming van tenminste vier andere rekenboeken is gebruikt. Bockstaele62 schrijft over D-Hoe-1537 dat het door zijn degelijkheid en wegens de verscheidenheid van onderwerpen die erin worden behandeld, een bijzondere plaats inneemt onder de mathematische werken die voor 1550 in de Nederlanden verschenen zijn. Omdat het echter in de volkstaal geschreven is, heeft het nooit de verspreiding en het succes gekend van het enkele jaren later verschenen Latijnse rekenboek van Gemma Frisius.63 Inderdaad is het werk van Frisius in de zestiende eeuw maar liefst 66 keer uitgegeven.64 Hiermee staan de twee uitgaven van het

werk van Van den Hoecke in schril contrast.65 Daarentegen bewijzen de latere rekenboeken waarin gebruik is gemaakt van D-Hoe-1537 - en mogelijk zijn dat er meer geweest dan de vier overgeleverde - dat het werk van Van den Hoecke wel degelijk een rol gespeeld heeft in de zestiende-eeuwse rekenkunde.

6.3 Mennher, 1550-73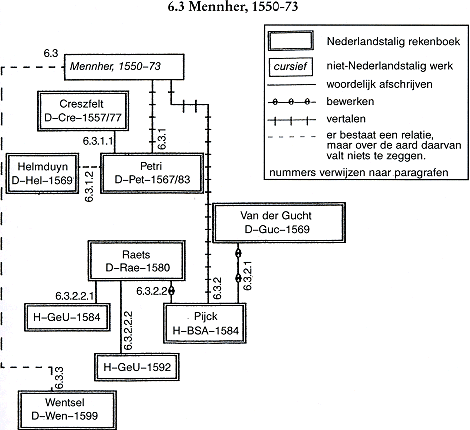



illustratie
Figuur 6.3. Het netwerk van relaties rond Mennher, 1550-73.


Valentin Mennher, afkomstig uit Duitsland, maar woonachtig te Antwerpen, liet in de periode van 1550 tot 1573 acht rekenboeken verschijnen, zeven in het Frans en één in het Duits. Het achtste verscheen na zijn dood en werd verzorgd door Michiel Coignet. Verschillende auteurs van Nederlandstalige rekenboeken blijken het werk van Mennher te kennen en te gebruiken.

6.3.1 D-Pet-1567/83

Petri publiceerde in 1567 een rekenboek. Dat werd in 1583 herdrukt, uitgebreid

met een gedeelte over algebra. Dit algebraïsche gedeelte is vrijwel geheel afkomstig uit het rekenboek van Mennher uit 1565.66

6.3.1.1 D-Cre-1557/77

Petri heeft nog andere bronnen gebruikt, onder andere een verloren gegaan werk van Creszfelt. Creszfelt vermeldt in zijn rekenboek van 1577 dat zijn boek een herdruk is van een eerdere uitgave. Op de titelpagina prijkt een portret van Creszfelt met het jaartal 1557. Mogelijk is de verloren gegane, eerste druk van het rekenboek van Creszfelt in 1557 verschenen. Petri heeft Creszfelt misschien persoonlijk gekend. Ze kwamen beiden uit Deventer. In ieder geval vertoont het voorwoord van het rekenboek van Creszfelt grote overeenkomsten met het voorwoord van het rekenboek van Petri uit 1567.

6.3.1.2 D-Hel-1569

Er bestaat eveneens een relatie tussen het werk van Petri en het rekenboek van Helmduyn. Onder de proloog in D-Hel-1569 staat het jaartal 1569. Dat is dus waarschijnlijk het jaar waarin dit rekenboek gedrukt werd. Uit de titel blijkt dat het geen eerste druk is. Er staat: Op nieus ghecorrigeert ende verbetert door P.V.B. Het is niet bekend wie deze P.V.B. is. De overeenkomsten tussen D-Pet-1567 en D-Hel-1569 bestaan misschien ook wel tussen D-Pet-1567 en de eerdere druk van het werk van Helmduyn. Deze eerste druk is mogelijk al voor 1567 verschenen. De vraag is wat precies het verband is tussen het werk van Helmduyn en dat van Petri.

Tussen D-Pet-1567 en D-Hel-1569 bestaan de volgende overeenkomsten.

- In beide werken komen verwante passages voor in de uitleg van numeratie en de regula falsi. Ze zijn niet woordelijk hetzelfde, zoals blijkt uit het volgende voorbeeld uit het hoofdstuk over numeratie. Petri schrijft:

Soe men wil scrijven een+
ghetal sonder duysendt,
hondert, tyne ofte eene, soo+
sette daer voor een O. Als+
wanneer ghy schrijven wilt+
achtduysent ende veertich,
soo moste ghy het alsoo
schrijven: 8040.+67

Helmduyn schrijft:

Soo wanneer men een ghetal
sonder duysent, hondert,
thien ofte een schrijven wil,
soo moetmen inde uytghelaten+
plaets een O setten. Als
wildy schrijven vierduysent+
ende tachtich, soo schrijftet
aldus: 4080.+68

- In beide rekenboeken wordt bij de behandeling van de omgekeerde regel van drieën een vergelijkbaar vraagstuk opgelost.69 Beide auteurs beginnen met: Item een stat heeft gheordonneert... De vraag is hoeveel een brood moet wegen als de prijs gelijk moet blijven en de korenprijs varieert. Bij Petri wordt het koren goedkoper, bij Helmduyn duurder. Ieder berekent vervolgens het juiste antwoord bij zijn eigen vraagstuk.

- Beide auteurs behandelen bij hun uitleg van de hoofdbewerking delen voorbeelden die het omgekeerde zijn van de voorbeelden die bij de uitleg van de hoofdbewerking vermenigvuldigen zijn gebruikt.

Petri behandelt bijvoorbeeld bij vermenigvuldigen:

768 × 6 = 4608, 768 × 7 = 5376, 768 × 8 = 6144, enz.

en bij delen:

4608:6 = 768, 5376:7 = 768, 6144:8 = 768, enz.70

Helmduyn hanteert hetzelfde principe, maar gebruikt andere getallen. Bij vermenigvuldigen berekent hij:

348 × 6 = 2088, 348 × 7 = 2436, 348 × 8 = 2784, enz.

en bij delen:

2088:6 = 348, 2436:7 = 348, 2784:8 = 348, enz.71

- Petri en Helmduyn plaatsen beiden de tafels van vermenigvuldiging aan het begin van hun werk, direct na de uitleg van numeratie. Het gaat in beide gevallen om een vierkant schema van 12 bij 12 met het opschrift Tabula Pytagorae. Dergelijke vierkante tafelschema's komen wel vaker voor. In H-GrU-1558, D-Sto-1595 en D-Wen-1599 worden de tafels van vermenigvuldiging eveneens met Pythagoras in verband gebracht. De plaats van de tafels aan het begin van het rekenboek is niet gebruikelijk, maar in H-TSB-1578 en D-Sto-1595 staan ze daar ook.

- In beide rekenboeken ontbreken de zeven- en de negenproef. Berekeningen worden sporadisch gecontroleerd. Daarmee onderscheiden Helmduyn en Petri zich van hun collega's, die juist erg veel aandacht besteden aan het controleren van berekeningen.

 

Dat er een verband bestaat tussen de rekenboeken van Petri en Helmduyn is hiermee wel aangetoond, maar over de aard van dit verband bestaat geen duidelijkheid. Misschien heeft Petri zich door het werk van Helmduyn laten inspireren, misschien ging het andersom. Het kan ook zijn dat beide auteurs uit een gemeenschappelijke bron hebben geput.

6.3.2 H-BSA-1584

Het werk van Mennher is ook gebruikt door Pijck, de auteur van H-BSA-1584. Pijck behandelt 140 vraagstukken die uit het werk van Mennher afkomstig zijn. Ze komen voor bij de regel van drieën met gehele en gebroken getallen en bij Rekeninghe van cassiers. Pijck heeft ook gebruik gemaakt van D-Guc-1569 en D-Rae-1580. In zijn uitvoerige inhoudsopgave vermeldt hij tamelijk consequent de herkomst van zijn vraagstukken. Dat herhaalt hij op de desbetreffende plaats in zijn rekenboek. Bij elk onderwerp geeft hij aan hoeveel vraagstukken hij uit de verschillende bronnen heeft overgenomen. Het gaat in het totaal om enkele honderden vraagstukken. Enkele voorbeelden van zijn bronvermeldingen zijn:

Van aender, verscheyden
exempelen van Mr. Valentijn+
Mennher de Kempten.72

Diversche questien op den
reghel van dryen uut Adriaen+
Gucht Vlaminck.73

Hiernaer volghen sommighe+
ander additien genomen uut+
Willem Raets Maestrichter.74

6.3.2.1 D-Guc-1569

In H-BSA-1584 komen 29 vraagstukken voor die overgenomen zijn uit D-Guc-1569. Het gaat om vraagstukken bij de regel van drieën met gehele getallen en bij de Welsche of Italiaanse praktijk. Ook voor sommige stukjes uitleg en theorie maakt Pijck gebruik van D-Guc-1569, alleen geeft hij op die momenten geen bronvermelding. Pijck springt vrij met zijn bron om. Sommige stukken neemt hij heel precies over, bijvoorbeeld als hij bij het aftrekken twee manieren van lenen uitlegt.75 Van der Gucht doet dat op woordelijk dezelfde wijze. Op andere plaatsen past hij de tekst uit zijn bron aan. Dat gebeurt onder andere bij de regel van drieën met benoemde getallen. Als op de eerste en de derde plaats in de regel een geldbedrag staat, moeten beide bedragen in dezelfde muntsoort zijn uitgedrukt. Van der Gucht formuleert dat als volgt:

Het mocht wel ghebueren, dat+
den eersten ende derden
ghetale niet ghelijck en
zouden zijn ende nochtans van
eender secten. Alsdan salmen+
den derden maken als den
eersten, ofte den eersten als
den derden.76

Pijck schrijft:

Alst gebeurt, dat het eerste+
ende het derde malcanderen+
niet gelijck en zijn van name
nochtans van eender natuere,+
dan salmense beyde van eender
name maken.+77

Pijck kiest uit zijn bron wat hij kan gebruiken en de rest laat hij weg. Van de vier vermenigvuldigtabellen die Van der Gucht geeft, neemt hij er twee over. Complementair vermenigvuldigen behandelt hij niet. Van de definitie voor de hoofdbewerking delen neemt hij slechts een gedeelte over. Kortom, van slaafs en kritiekloos overschrijven is nergens sprake.78

6.3.2.2 D-Rae-1580

De belangrijkste bron die Pijck voor H-BSA-1584 gebruikt heeft, is D-Rae-1580. In beide rekenboeken komen dezelfde onderwerpen in dezelfde volgorde aan bod. De rekenregels hebben dezelfde namen. Pijck neemt vele vraagstukken uit D-Rae-1580 over, maar voegt daar uitwerkingen, proeven en stukjes uitleg aan toe. Beide auteurs behandelen bijvoorbeeld het algoritme van Euclides, dat gebruikt wordt om breuken te vereenvoudigen.

 

Om de breuk 108/144 te vereenvoudigen schrijft Raets:

Divideert 144 met 108, so+
blijvender noch te divideren
36. Waer mede dat divideert+
108, soo blijfter niet over.+

Daerom so abbrevieert die 108/144+
met 36, comt als boven ¾.+79

Pijck behandelt ditzelfde voorbeeld, maar geeft uitleg vooraf:

Om het vorsen getal te vinden,+
soo machmen oock het meeste+
getal divideren doir het+
minste, soo langhe tot datmen+
come tot een divisie sonder
reste. Ende den divisoir oft+
deylder van sulcker divisie+
is het getal daermen het+
gebroken mede minderen moet.+80

Daarna volgt pas het voorbeeld. Deze uitleg komt noch in D-Rae-1580, noch in D-Guc-1569, noch in het werk van Mennher voor en is mogelijk door Pijck zelf bedacht.

6.3.2.2.1 H-GeU-1584

D-Rae-1580, het rekenboek van Raets, is niet alleen door Pijck gebruikt, maar ook door de auteur van H-GeU-1584. De definities van numeratie en optellen komen woordelijk overeen en verder wordt de optelling van 345 en 898 in beide rekenboeken op overeenkomstige wijze uitgelegd. Meer overeenkomsten zijn er niet. De auteur van H-GeU-1584 heeft vermoedelijk naast D-Rae-1580 ook nog andere bronnen gebruikt, maar die zijn niet bekend.

6.3.2.2.2 H-GeU-1592

Ook de auteur van H-GeU-1592 heeft fragmenten uit D-Rae-1580 overgenomen. Enkele daarvan komen ook in H-GeU-1584 voor, maar dat geldt lang niet voor alle overeenkomstige passages. De auteur van H-GeU-1592 heeft dus vermoedelijk rechtstreeks gebruik gemaakt van D-Rae-1580 en niet indirect via H-GeU-1584. Overeenkomstig zijn de definities van de hoofdbewerkingen met uitzondering van delen, want die hoofdbewerking wordt in H-GeU-1592 niet behandeld. Verder zijn er 48 overeenkomstige vraagstukken. Ze worden vooral in het tweede deel van de rekenboeken aangetroffen, waar het gaat om de praktische toepassingen van de rekenkunde. In H-GeU-1592 staat bij deze vraagstukken alleen een berekening, terwijl daar in D-Rae-1580 nog enige uitleg aan toegevoegd is. In D-Rae-1580 komen veel vraagstukken voor die niet in H-GeU-1592 zijn opgenomen. Het omgekeerde geldt ook. Dat doet vermoeden dat ook de auteur van H-GeU-1592 naast D-Rae-1580 nog andere bronnen gebruikt heeft.

6.3.3 D-Wen-1599

Wentsel laat in zijn rekenboek blijken dat hij het werk van Mennher kent. Bij een van zijn vraagstukken schrijft hij:

Doch in des Menhers boeck, by
zijn leven anno 1565+
uutghegaen, vinde ick dat+
Menher dese selve questie
verhandeldt.+81

Hoewel Wentsel het werk van Mennher blijkbaar gelezen heeft, heeft hij er geen zaken rechtstreeks uit overgenomen.

6.4 H-BKB-1568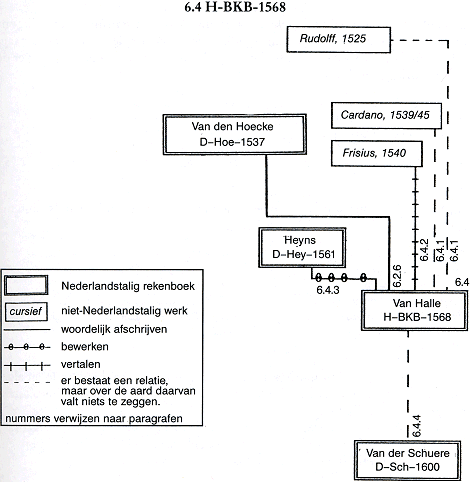



illustratie
Figuur 6.4. Het netwerk van relaties rond H-BKB-1568.


Van Halle is de auteur van H-BKB-1568. Het is een uitvoerig rekenboek met veel uitgewerkte en gecontroleerde vraagstukken en veel rekenregels. Wiskundige onderwerpen die slechts zelden in rekenboeken voorkomen, gaat Van Halle niet uit de weg, zoals verhoudingen, algebra en het indelen van getallen in allerlei klassen. Uit zijn rekenboek blijkt dat hij het werk van verschillende voorgangers geraadpleegd heeft. Zo meldt hij bijvoorbeeld:

Int sypher syn 4 specien...+
ende niet 7 ghelijck als die+
andere boexkens hebben.82

6.4.1 Rudolff en Cardano

Van Halle heeft niet uitsluitend Nederlandstalige bronnen gebruikt. Dat blijkt onder andere bij het behandelen van de rekenregels. Naast de Nederlandse naam geeft hij meestal ook de Franse, Italiaanse en Latijnse naam van de regel. Over de regel van drieën schrijft hij bijvoorbeeld:

Dese reegel is gheheeten int+
Latyn ‘regula tryum’, int
Italiaensche ‘regula de tri’,
int Francoijs ‘reigle de+
trois’, int Duytsche ‘regel+
van drijen’.83

Aan het eind van het hoofdstuk over algebra worden twee buitenlandse auteurs genoemd.

Van welke voirscreven regulen
in dyen ghy verstant begheert
te hebbene, soo leest+
Cristophorum Jauier ende
Hieronimium Cardanum welke+
van den regula cos breeder+
ghescreven hebben.84

In 1525 verscheen er van Christoff Rudolff een boek over rekenkunde en algebra.85 Het werd door Van den Hoecke gebruikt.86 Van Halle zou eveneens uit deze bron geput kunnen hebben.

Geronimo Cardano schreef zowel in 1539 als in 1545 een boek over algebra.87 Het is niet duidelijk naar welk van de twee boeken Van Halle verwijst in bovenstaand citaat en wat hij misschien aan Cardano ontleend heeft.

6.4.2 Frisius

Bij de regel van valse positie meldt Van Halle:

Doctor Gemma noempt die regula+
falsi van eender positien te
wesen, soe wanneer men daer+
inne maer een hipothese en
stelt. Dat is alsmen maer+
eens en geraet.+88

Van Halle blijkt het rekenboek van Gemma Frisius goed te kennen.89 Hij heeft er uitvoerig uit geput, waarbij hij allerlei keuzes maakte. In de hoofdstukken over de vier hoofdbewerkingen heeft Van Halle slechts één vraagstuk van Frisius overgenomen, samen met een driehoekige schema met de tafels van vermenigvuldiging. In het breukenhoofdstuk gebruikt Frisius een meetkundig figuur om de vermenigvuldiging van ¾ × ⅔ × 6/7 visueel voor te stellen.90 Dezelfde tekening komt bij Van Halle voor. Bij de behandeling van de verschillende rekenregels gebruikt Van Halle 12 vraagstukken uit het werk van Frisius.

De grootste overeenkomsten tussen dit Latijnse rekenboek en H-BKB-1568 zijn te vinden in de hoofdstukken over het trekken van de tweede- en derdemachtswortel, verhoudingen en het berekenen van de middelevenredige. Van Halle heeft deze hoofdstukken woordelijk vertaald en ook de berekeningen nauwkeurig overgeschreven. Op fol. 161r bevindt zich de enige plek waarop hij iets toevoegt aan de fragmenten die hij uit het werk van Frisius overneemt. Bij het vraagstuk over de lengte van een ladder die tegen een toren staat, maakt hij een prachtige, gedetailleerde illustratie.91

Zonder twijfel heeft Van Halle intensief gebruik gemaakt van het rekenboek van Frisius. Toch is dit rekenboek niet de enige Latijnse bron die hij gehanteerd heeft. In het hoofdstuk over getaltheorie92 wemelt het van de Latijnse citaten. Getaltheorie wordt door Frisius niet behandeld en deze citaten zijn dus waarschijnlijk uit een andere, tot nu toe onbekende Latijnse bron afkomstig.

Op fol. 161v noemt Van Halle de naam Euclides. Deze blijkt overgenomen te zijn uit een overeenkomstige passage in het rekenboek van Frisius. Van Halle heeft de Elementen van Euclides waarschijnlijk niet rechtstreeks zelf gebruikt voor zijn rekenboek.

D-Hoe-1537

Al eerder is vermeld dat Van Halle bij de uitleg van de regula falsi Van den Hoecke noemt. Er zijn verschillende overeenkomstige passages in H-BKB-1568 en D-Hoe-1537. Het rekenen met algebraïsche vormen, inclusief het ongebruikelijke notatiesysteem, komt woordelijk overeen en geeft het sterke vermoeden dat D-Hoe-1537 een bron is geweest voor H-BKB-1568.93

6.4.3 D-Hey-1561

Een andere bron die Van Halle mogelijk gebruikt heeft, is het rekenboek van Heyns.94 Heyns begint zijn hoofdstuk over numeratie met een bladzijde die in drieën is gedeeld. In die drie delen worden respectievelijk digiten, articulen en compositen behandeld. De getalsnamen zijn dwars op de getalsymbolen afgedrukt. Deze bladzijde komt precies zo voor in H-BKB-1568. Bij de tafels van ver-

menigvuldiging noteren beide auteurs hetzelfde rijmpje:

Die Opt reekenen wilt+
veerdich ghepast sijn,+
moet sulke tafelen van
buytens vast sijn.+95

Bij vermenigvuldigen en delen behandelt Van Halle zeven vraagstukken die woordelijk overeenkomen met vraagstukken uit het werk van Heyns. Bij de regel van drieën zijn maar liefst 45 overeenkomstige vraagstukken. Als Van Halle D-Hey-1561 als bron gebruikt heeft, is hij er vrij mee omgesprongen. Hij neemt veel, maar niet alle vraagstukken over. Hij verandert de volgorde en voegt uitwerkingen en controles toe. Het is niet bekend welke bronnen Heyns bij de samenstelling van zijn werk gebruikt heeft.

6.4.4 D-Sch-1600

Er bestaat mogelijk een relatie tussen H-BKB-1568 en D-Sch-1600. Van Halle en Van der Schuere zijn namelijk de enige twee auteurs die een overzicht behandelen van de verschillende verhoudingen die tussen twee getallen kunnen bestaan. Er is geen woordelijke overeenkomst tussen beide overzichten, maar het is wel frappant dat ze allebei dezelfde fout bevatten: Submultiplex Superparticularis in plaats van Submultiplex Subsuperparticularis.96 Bovendien zijn Van Halle en Van der Schuere de twee auteurs die opvallend veel rekenkundige rijmpjes in hun tekst hebben opgenomen, veel meer dan hun collega's, die meestal alleen in hun voorwoord en bij de tafels van vermenigvuldiging berijmde teksten hebben. Deze rijmpjes komen niet overeen, maar het zou kunnen zijn dat Van der Schuere door het rekenboek van Van Halle op een idee is gebracht. Overigens is het ook hier niet uitgesloten dat beide auteurs een gemeenschappelijke (buitenlandse) bron gebruikt hebben.

Verdere bronnen van D-Sch-1600 zijn niet gevonden. De terminologie van Van der Schuere verraadt af en toe een Franse herkomst: soubstraheren, soubstractio, douzijn, divisoir. Wellicht heeft Van der Schuere een Frans rekenboek als bron gebruikt.

6.5 D-Dij-1591

D-Dij-1591 is een verzameling vraagstukken met antwoorden. Noch het penningrekenen, noch het rekenen met Hindoe-Arabische cijfers wordt er uitgelegd.



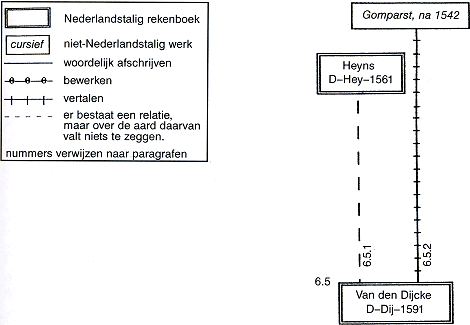illustratie
Figuur 6.5. Het netwerk van relaties rond D-Dij-1591.


In het hoofdstuk over optellen komt bijvoorbeeld de volgende optelling voor:

Aert 15
Louis 24
Anth. 35
Giles 48
Claes 59
Jehan 61
Joris 72
Lucas 88
Alex 99
_____ ___
facit+ 50197

Er wordt niet uitgelegd hoe het antwoord is verkregen. Het kan zowel door middel van penningrekenen als door cijferen gevonden zijn, hoewel de wijze waarop de getallen precies onder elkaar zijn geplaatst, doet vermoeden dat de laatste methode gebruikt is.

6.5.1 D-Hey-1561

Er lijkt een verband te bestaan tussen D-Dij-1591 en D-Hey-1561. Ook Heyns heeft in zijn rekenboek nergens een uitwerking aan zijn vraagstukken toegevoegd.98 Er is grote overeenkomst tussen bepaalde vraagstukken uit D-Dij-1591

en D-Hey-1561 wat inkleding betreft, maar de getallen verschillen. Heyns heeft bijvoorbeeld het volgende vraagstuk:

Alsmen op een uere maect 234,+
456, 678, 890 oft 1987
spellen, hoeveel in 6751+
ueren?+99

Van den Dijcke heeft:

Alsmen op een ure maeckt 237,
349, 458, 367 spellen etc.,
hoeveel in 7869 uren?100

Een ander gelijksoortig vraagstuk uit beide rekenboeken:

345, 456, 789,...
crijghsknechten hebben veur+
solt 2712390, 3585072,+
6203118, ...croonen. Hoe veel
is elcks deel daer af? Facit:+
7862 croonen.101

Soe 1234, 5678, 6970,...
crijgsknechten hebben voor
solt 12162304, 55962368,
68696320 ... ducaten.102

De vraagstelling en het antwoord ontbreken in D-Dij-1591.

In het totaal zijn er in beide rekenboeken 17 vergelijkbare vraagstukken te vinden: 3 bij vermenigvuldigen, 3 bij delen en 11 bij de regel van drieën met gehele getallen. Omdat deze vraagstukken niet woordelijk overeenkomen, is de relatie tussen het werk van Heyns en dat van Van den Dijcke moeilijk nader vast te stellen. Misschien heeft Van den Dijcke zijn bron bewerkt, maar het is ook mogelijk dat hij een bewerking van D-Hey-1561 heeft geraadpleegd. Ook hier is het niet uitgesloten dat D-Hey-1561 en D-Dij-1591 beide teruggaan op een gemeenschappelijke (buitenlandse) bron.

6.5.2 Gomparst

D-Dij-1591 bevat in ieder geval honderden vraagstukken die niets met D-Hey-1561 te maken hebben. Deze zijn afkomstig uit het Franse rekenboek van Godevaert Gomparst, een schoolmeester uit Antwerpen.103 Van den Dijcke vermeldt op zijn titelpagina:

Ghevonden ende voorghehouden+
bij wijlen M. Godevaert+
Gomparst.104

Nijhoff en Kronenberg dateren het rekenboek van Gomparst rond 1535,105 maar dat is aanvechtbaar. In verschillende vraagstukken in zijn rekenboek noteert Gomparst een jaartal. Bijvoorbeeld: Troix bourgeoys au 16e Mars anno 38 ... of Anno 40 du facteur de la Royale Maieste de Portugal.... Het jaartal 1535 komt maar een keer in de tekst voor. Het vroegste genoemde jaartal is 1542: Anno 42 a la quaresme changoient deux condeurs...106 Het is niet erg waarschijnlijk dat een auteur in zijn rekenboek ‘toekomstige’ jaartallen gebruikt. Het rekenboek is dus vrijwel zeker na 1542 gedrukt.

Dat lijkt ook om andere redenen aannemelijk. Gomparst was in de jaren veertig nog steeds schoolmeester. Hij is deken geweest van het gilde van Antwerpse schoolmeesters in 1531-32 en in 1547-48.107 Symon Cock herdrukte in 1545 het rekenboek van Van den Hoecke en kan dus ook rond deze tijd het rekenboek van Gomparst hebben gedrukt. Van den Dijcke suggereert zelfs 1551 als mogelijke datering van zijn bron. Zijn rekenboek is uit 1591. In zijn voorrede schrijft hij over de regel van winst en verlies dat deze pas sinds kort bekend is geworden dankzij:

sommige liefhebbers der
consten, onder de welcke Mr.+
Godevaert Gomparst, excellent
arithmeticien in Antwerpen,+
over 40 jaeren het+
principaelste deel heeft+
gevonden ende daerna door my
eerst gesolveert.+108

Hoe oud zijn bron ook mag zijn, Van den Dijcke heeft in ieder geval vele vraagstukken inclusief de jaartallen ongewijzigd uit het werk van Gomparst overgenomen.

6.5.3 D-Sto-1595

Boven de tafels van vermenigvuldiging noteert Stockmans het volgende rijmpje:

Die door het cyfferen wilt
komen ter eeren,+
moet wel vast dees tafel van+
buyten leeren.109

Van den Dijcke heeft hetzelfde rijmpje. Verder zijn er geen overeenkomsten tussen D-Sto-1595 en D-Dij-1591 aangetroffen. Het is niet verantwoord om op basis van dit ene rijmpje conclusies te trekken over een relatie tussen beide rekenboeken. Rijmpjes worden nu eenmaal makkelijk uit het hoofd geleerd en kunnen

los van het rekenboek een eigen leven gaan leiden. Stockmans heeft misschien ooit het rijmpje uit het werk van Van den Dijcke geleerd zonder dat hij dit werk heeft ingezien.

6.6 Rekenhandschriften

Van vijf rekenboeken kan geen directe relatie met een van de overige werken uit het corpus worden vastgesteld. Het blijken alle vijf handschriften te zijn.110 Hierdoor wordt misschien de indruk gewekt dat de rekenhandschriften een aparte groep vormen, die weinig banden heeft met de gedrukte boeken. Dit vermoeden is onjuist. Eerder is gebleken dat er in ieder geval zeven rekenhandschriften in het corpus voorkomen die wel banden hebben met een of meer gedrukte bronnen.111 Bovendien passen de vijf manuscripten qua inhoud in de traditie van de rekenboeken. Slechts H-BaU-1445 wijkt in bepaalde opzichten enigszins af.112

Van de vijf manuscripten in kwestie zijn er drie uit de vijftiende eeuw. Eventueel gebruikte bronnen zouden nog ouder moeten zijn. Vermoedelijk zouden dat dan Latijnse of Duitse bronnen zijn. De drie vijftiende-eeuwse rekenboeken zijn gering van omvang. Het gaat om twee fragmenten en een volledig rekenboek.

6.6.1 H-BaU-1445

H-BaU-1445 is een volledig rekenboek. Het is een klein tractaat van 6 folia waarop numeratie, optellen, aftrekken, halveren, verdubbelen, vermenigvuldigen, delen en worteltrekken worden uitgelegd. Opvallend is dat in dit rekenboek het rekenen met breuken niet wordt behandeld. Verder ontbreken de rekenregels en worden er slechts ‘kale’ berekeningen uitgevoerd. Dat wil zeggen, er is nergens sprake van een ingekleed vraagstuk of een berekening met munten, maten of gewichten. Eigenlijk past dit rekenboek meer in de traditie van de eerste Latijnse rekenboeken over het rekenen met Hindoe-Arabische getallen, de algorismustractaten, zoals bijvoorbeeld het rekenkundige werk van Sacrobosco.113 In deze Latijnse rekenboeken gaat het niet om de praktische toepassingen van de rekenkunde.

Ook H-BaU-1445 lijkt niet voor koop-en ambachtslieden te zijn geschreven. De praktische vraagstukken ontbreken. De slotwoorden van het navolgende tractaat in dezelfde band wekken de indruk dat er van een andere doelgroep sprake is. In dezelfde hand staat op fol. 180v geschreven:

Deo gratias affinitus et
completus per me Bernardum
studentem temporis tunc
Hildesim anno domini
mccccxlv.114
God zij dank, [het onderwerp ontbreekt, maar dat is mogelijk dit boek] is beëindigd en voltooid door mij Bernardus, die toentertijd studeerde in Hildesheim in het jaar des Heren 1445.

Het rekentractaat is dus geschreven door een zekere Bernard te Hildesheim. Het is bijzonder dat een dergelijk rekenboek niet in het Latijn, maar in de volkstaal is geschreven. Overigens is de volkstaal in het rekenboek doorspekt met Latijnse rekentermen.

6.6.2 H-KHA-1453

H-KHA-1453 is een fragment van zeven folia, waarop koopmansvraagstukken met de regel van drieën worden opgelost.

6.6.3 H-BrS-1463

De zes folia van H-BrS-1463 zijn gevuld met de regel van gezelschap, de regel van winst en verlies, de ruilregel en de regel van reeksen. Ook het klassieke vraagstuk van de man die op zijn sterfbed zijn testament maakt terwijl zijn vrouw in verwachting is, komt hier voor.115

 

Deze gebruikelijke rekenkundige onderwerpen komen ook voor in de twee ‘losse’ manuscripten uit de zestiende eeuw, H-ANE-1562 en H-TSB-1578, die veel omvangrijker zijn dan de vijftiende-eeuwse. Net als in de gedrukte rekenboeken komen de hoofdbewerkingen voor gehele getallen en breuken aan de orde, de rekenregels en vele praktische vraagstukken. Ze bevatten allebei enkele Franse fragmenten en gaan dus mogelijk terug op Franse bronnen.

6.6.4 H-ANE-1562

Heyndrik Nouts begint zijn rekenboek met de mededeling:

Ceste livre appertient a moy,
Heyndrik Nouts, 1562.

Hij vertaalt deze uitspraak in het Nederlands en in nog een andere taal, vermoedelijk Portugees, maar de tekst op de eerste pagina is vrijwel onleesbaar geworden. Een vergelijkbare aanhef wordt aangetroffen in H-GeU-1584:

Ceste livre appertient a moy,
Josse Verniers, anno 1584.

en in H-BSA-1584:

Dese sijfverboeck behoort toe
Cornelis Pijck, 1584.

Het is kennelijk een gebruikelijk begin van een rekentractaat, vergelijkbaar met de wijze waarop leerlingen tegenwoordig hun naam op een schoolschrift zetten. Dit eigendomsmerk wordt ook in niet-rekenkundige handschriften aangetroffen. In gedrukte rekenboeken komt het niet voor. Misschien mag eruit worden afgeleid dat deze manuscripten louter voor eigen gebruik geschreven zijn.

Dit vermoeden geldt vooral voor H-ANE-1562 zeer sterk. Eerder is al opgemerkt dat Nouts zijn rekenboek schreef in de periode van 1562 tot 1582.116 Hij heeft in die tijd een groot aantal vraagstukken verzameld. Deze zijn voorzien van een gecijferde oplossing, maar elke toelichting ontbreekt. Het lijkt erop dat hij in de loop van de tijd aantekeningen voor persoonlijk gebruik heeft gemaakt.

6.6.5 H-TSB-1578

In de ‘Practiicke om lichtelyck te leeren ciffer in gantsche ende gebroke’ is de bekende rekenkundige stof hier en daar opgefleurd met een versierde kapitaal aan het begin van een hoofdstuk. Het is niet bekend op welke voorganger de onbekende auteur of scribent zich baseert.

 

Voorlopig is het nog onbekend welke bronnen gebruikt zijn door de auteurs of scribenten van de voorgaande vijf rekenmanuscripten. Het is evenmin duidelijk of deze tractaten misschien als bron gebruikt zijn voor latere rekenboeken. Met de overige rekenboeken uit het corpus kan in ieder geval geen verband aangetoond worden.

Ten slotte

In figuur 6.6 zijn alle verbanden weergegeven die gevonden zijn tussen de Nederlandstalige rekenboeken onderling en tussen deze rekenboeken en niet-Nederlandstalige werken. De vijf rekenboeken die tot nu toe aan geen enkel ander werk gerelateerd kunnen worden, zijn niet in het schema opgenomen. Hetzelfde geldt voor ongewijzigde herdrukken van de rekenboeken.

Uit het voorgaande onderzoek blijkt dat vrijwel alle auteurs van de rekenboeken bij het schrijven van hun werk gebruik hebben gemaakt van een of meer bronnen. Die bronnen zijn meestal Nederlandstalig, maar kunnen soms ook in een andere taal geschreven zijn.

De wijze waarop de auteurs met hun bronnen omspringen verschilt nogal. Geen enkele keer is er een bron volledig afgeschreven of vertaald, maar sommige auteurs maken toch wel op tamelijk grote schaal van hun bron gebruik. De scribent van H-GrU-1558 schrijft 123 van de 176 folia uit D-Hoe-1537 over. Van den Dijcke, - auteur van D-Dij-1591 - vertaalt enkele honderden vraagstukken uit het reken-



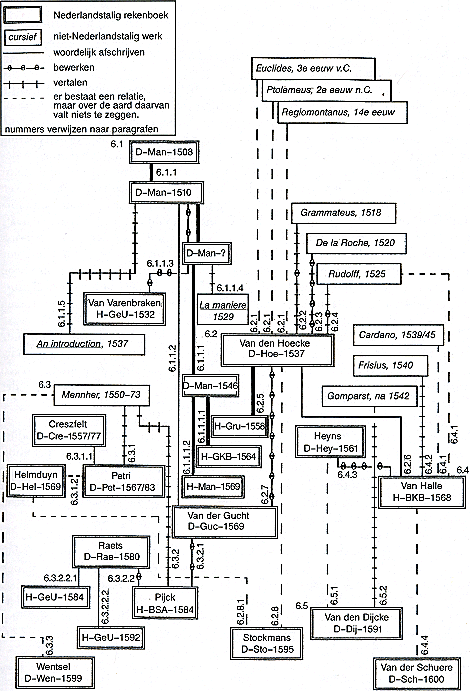illustratie
Figuur 6.6. Het netwerk van alle gevonden relaties tussen de Nederlandstalige rekenboeken onderling en tussen deze rekenboeken en niet-Nederlandstalige werken.


boek van Gomparst. Petri en Van Halle nemen een volledig algebra-hoofdstuk uit hun bron over. Andere auteurs putten wat minder uitvoerig uit hun bronnen en ontlenen alleen een aantal vraagstukken. Een enkeling gebruikt het werk van een voorganger op zeer beperkte wijze: Van der Gucht ontleent slechts vier vraagstukken aan D-Man-1510.

Soms wordt een bron woordelijk afgeschreven. Het eerdergenoemde hoofdstuk over algebra in H-BKB-1568 is bijvoorbeeld vrijwel woordelijk gelijk aan het algebra-hoofdstuk in D-Hoe-1537. Soms springt een auteur wat vrijer met zijn bron om, dan is er sprake van bewerken. Dat is bijvoorbeeld een goede typering van de werkwijze van Pijck. In zijn rekenboek neemt hij sommige zaken woordelijk over uit D-Guc-1569, maar op andere momenten herformuleert hij de tekst uit zijn bron of laat hij stukjes weg. Een enkele keer hebben twee rekenboeken weliswaar overeenkomstige tekstgedeelten, maar zijn er zoveel verschillen in formulering dat de relatie tussen beide werken niet duidelijk is. Men kan zich dan afvragen of dat ene rekenboek wel een bron van het andere is geweest. Er zou ook sprake kunnen zijn van een gemeenschappelijke (buitenlandse) bron die beide auteurs onafhankelijk van elkaar gebruikt hebben. Zolang die buitenlandse bron niet gevonden is, blijft dat onzeker. Een dergelijke relatie bestaat bijvoorbeeld tussen D-Sto-1595 en D-Hel-1569, tussen D-Sto-1595 en D-Hoe-1537 en tussen D-Dij-1591 en D-Hey-1561.

Verschillende auteurs maken van hun werk een compilatie van verschillende bronnen. Ze selecteren geschikte vraagstukken en fragmenten, passen waar nodig de tekst uit hun bronnen aan, voegen eigen bijdragen toe en componeren zo een nieuw rekenboek. Sommige rekenboeken zijn door deze werkwijze bijzonder omvangrijk geworden, bijvoorbeeld: H-BKB-1568 en H-BSA-1584.

Hoewel gebleken is dat vele auteurs bij de totstandkoming van hun rekenboek het werk van voorgangers gebruiken, maakt slechts een enkeling daar melding van. Dat vindt kennelijk niemand een probleem. In de rekenboeken wordt nooit een auteur van plagiaat beschuldigd en nooit pretendeert een auteur origineel te zijn. Daar is het de auteurs niet om begonnen.117 Ze willen zo eenvoudig, helder en goed mogelijk de rekenkunde onderwijzen. Als het werk van collega's daaraan kan bijdragen, wordt daar gebruik van gemaakt.

Nu duidelijk is geworden hoe zeer het in de zestiende eeuw gebruikelijk was om bij het schrijven van een rekenboek het werk van één of meer voorgangers te benutten, wordt het tijd om de algemeen heersende opvatting over het rekenboek van De la Roche enigzins bij te stellen.118 De la Roche kopieerde het grootste deel van zijn werk uit een handschrift van zijn leermeester Nicolas Chuquet.119 In de literatuur wordt De la Roche - die de naam van Chuquet in zijn werk noemt - herhaaldelijk verweten dat hij plagiaat pleegt.120 Dit is een te ‘modern’ verwijt. De

la Roche was een kind van zijn tijd. Hij suggereert niet dat hij de inhoud van zijn rekenboek zelf bedacht heeft. Hij wil slechts - net als zijn collega's - zijn kennis op het gebied van de rekenkunde zo goed mogelijk doorgeven. Het gewaardeerde werk van zijn voorganger kan hierbij helpen.

 

Het netwerk van relaties tussen rekenboeken dat in dit hoofdstuk beschreven is, is gebaseerd op de vele overeenkomsten die tussen de rekenboeken bestaan. Het is terecht dat die overeenkomsten ruime aandacht krijgen, maar daaruit mag niet de indruk ontstaan, dat alle rekenboeken hetzelfde zijn en dat er geen sprake zou zijn van enige ontwikkeling gedurende de zestiende eeuw.

Binnen het sterk samenhangende corpus zijn (groepen van) rekenboeken aan te wijzen die zich in een bepaald opzicht onderscheiden van de rest. Zo wordt bijvoorbeeld een belangrijke groep van rekenboeken gevormd door de verschillende edities van Die maniere... In deze over het algemeen dunne boekjes, waarvan het eerste al in 1508 gedrukt werd, gaat het over elementaire rekenkunde, rekenregels, praktische vraagstukken en in veel gevallen komt het penningrekenen aan de orde.

In 1537 wordt het rekenboek van Van den Hoecke gedrukt. Men zou kunnen zeggen dat Van den Hoecke in zijn rekenboek meer ‘wetenschappelijke’ pretenties heeft dan de auteur van Die maniere... Hij maakt gebruik van bekende buitenlandse bronnen en hij behandelt onderwerpen als algebra, verhoudingen en de middelevenredige. Ook bij enkele auteurs die D-Hoe-1537 gebruikt hebben, komen deze ‘moeilijkere’ onderwerpen voor. Van Halle voegt er zelfs nog een soort getaltheorie aan toe, waarbij getallen in allerlei klassen ingedeeld worden. Ook Van der Schuere behandelt dit onderwerp en enkele andere meer wiskundige onderwerpen.

Overigens is het niet zo dat de eenvoudige en de meer wiskundige rekenboeken als twee aparte groepen naast elkaar blijven bestaan. In de tweede helft van de zestiende eeuw komen boeken voor die als het ware een mengvorm van beide soorten zijn, zoals bijvoorbeeld het rekenboek van Van Halle. Deze auteur sluit zich enerzijds aan bij de ‘wetenschappelijke’ opzet van Van de Hoecke door ook wat voir die gheleerde te seggene.121

Maar in hetzelfde rekenboek richt hij zich met zijn koopmanstabellen tot lezers die slechts getallen kunnen lezen en niet kunnen rekenen.122 Van der Gucht maakt weliswaar gebruik van D-Hoe-1537, maar behandelt geen onderwerpen die verder gaan dan de elementaire rekenkunde.

Naarmate de rekenboeken voor een bredere doelgroep geschreven lijken te zijn, dus zowel eenvoudige als ook moeilijkere onderwerpen bevatten, zijn ze omvangrijker. Zo beslaat bijvoorbeeld het rekenboek van Van Halle 303 folia, dat wil zeggen 606 pagina's en dat van Van der Schuere 408 pagina's. Deze aantallen vormen een groot contrast met bijvoorbeeld de 96 pagina's van D-Man-1508.

Ook het rekenboek van Stockmans is met 416 pagina's zeer omvangrijk. Dit wordt niet zozeer door de onderwerpkeuze veroorzaakt, als wel door de uitvoerige wijze waarop Stockmans uitleg geeft. Hij hoopt daarmee te bereiken dat zijn boek geschikt is voor zelfstudie.123

Naarmate de tijd verstrijkt, blijft het penningrekenen in de rekenboeken steeds vaker achterwege. Het komt weliswaar nog voor in het rekenboek van Petri uit 1598, maar in de overige rekenboeken uit de laatste decennia van de eeuw ontbreekt deze traditionele rekenmethode. Van Halle en Van der Gucht behandelen het nog wel, maar zij beperken zich tot de uitleg van het vermenigvuldigen en delen met penningen. Optellen en aftrekken wordt niet meer uitgelegd.124

Er zijn nog veel meer verschillen tussen de rekenboeken vast te stellen. Er zijn rekenboeken die speciaal voor de jeugd geschreven en er zijn rekenboeken die ook met een volwassen doelgroep rekening houden. Er zijn rekenboeken waarin elk vraagstuk uitvoerig voorgerekend en gecontroleerd wordt, terwijl in andere rekenboeken alleen maar antwoorden worden gegeven. Er zijn auteurs die namen noemen van door hen gebruikte bronnen en er zijn auteurs die dat achterwege laten. Sommige auteurs beschrijven hun oplossingen in uitvoerige volzinnen; andere passen grafische verkortingen toe. Er zijn gedrukte boeken waar latere auteurs herhaaldelijk uit geput hebben, en er zijn handschriften die vermoedelijk geen enkele maal als bron gebruikt zijn. Kortom: de verschillen tussen de rekenboeken uit het corpus zijn talrijk. Daarom zijn deze verschillen op een aantal plaatsen in deze studie aan de orde gesteld; verder onderzoek blijft nuttig.

Omdat de overeenkomsten tussen de rekenboeken echter talrijker en opvallender zijn, is daar - met name in dit hoofdstuk - in eerste instantie de aandacht naar uitgegaan. Uit het netwerk van relaties dat in dit hoofdstuk gepresenteerd wordt, komt een belangrijk uitgangspunt van de auteurs van de rekenboeken naar voren: wie een goed rekenboek wil schrijven, maakt daarbij gebruik van het werk van voorgangers.

 

In het volgende hoofdstuk zal blijken dat dit gebruik een belangrijke factor is geweest in de ontwikkeling van de Nederlandse rekentaal. Er wordt beschreven hoe de auteurs omsprongen met de rekentaal en rekentermen die ze in hun binnen- en buitenlandse bronnen aantroffen. Aan het eind van de zestiende eeuw is er nog steeds geen sprake van een vaste Nederlandse rekenterminologie. Maar hierna zal blijken dat de auteurs van de rekenboeken wel een belangrijke bijdrage hebben geleverd aan de ontwikkeling van de Nederlandse rekentaal.


Vorige Volgende