De macht van het woord

Een selectie uit het taalkundig werk van D.M. Bakker

[p. 103]

Volgorde in werkwoordsgroepen

In een vorige publikatie (Bakker 1977) heb ik aangetoond dat beschrijving van de volgorde in werkwoordsgroepen in termen van links van-relaties (-) slechts kon geschieden met behulp van twee verschillende graphs. De eerste graph ziet er als volgt uit:

G1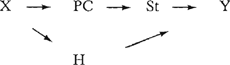

Hierin zijn X en Y niet-verbale elementen, die verder buiten beschouwing blijven; PC is een element als uit in het bos uit of uitbesteden. Het element St bevat de hoofdwerkwoordsstam, d.i. de stam van een zelfstandig of koppelwerkwoord. De graph geldt voor drie soorten werkwoordsgroepen:

1.	groepen waarin St een persoonsvorm (Pv) is;
2.	groepen waarin St een voltooid deelwoord (Vd) is en H een of meer hulpwerkwoorden (waaronder eventueel een Pv);
3.	groepen waarin St een infinitief (Inf) is en H de persoonsvorm van een hulpwerkwoord.

G1 verantwoordt o.a. de volgende werkwoordsgroepen:

(1)a	(dat Piet het werk)	uit	besteedt
b	(dat Piet het werk) zal	uit	besteden
c	(dat Piet het werk)	uit zal	besteden
d	(dat Piet het werk)	uit	besteden zal
e	(dat Piet het werk) heeft	uit	besteed
f	(dat Piet het werk)	uit heeft	besteed
g	(dat Piet het werk)	uit	besteed heeft
h	(dat Piet het werk) zou kunnen hebben	uit	besteed
i	(dat Piet het werk)	uit z.k.h.	besteed
j	(dat Piet het werk)	uit	besteed z.k.h.

De tweede graph verantwoordt de volgordemogelijkheden van werkwoordsgroepen waarin de vulling van H bestaat uit één of meer infinitieven, al dan niet voorafgegaan door een Pv, en waarin St een Inf is.

[p. 104]

G2

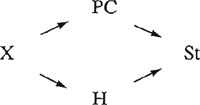Deze graph verantwoordt groepen als

(2)	a (dat Piet het werk) zou hebben kunnen uit besteden b (dat Piet het werk) uit zou hebben kunnen besteden

Uitgesloten worden met name groepen als

(3)	a *(dat Piet het werk) zou uit hebben kunnen besteden b *(dat Piet het werk) zou hebben uit kunnen besteden

Deze uitsluiting is equivalent aan de assumptie, dat een Pv en één of meer Inf's deel uitmakend van H een ondoordringbare groep vormen met intern vaste volgorde. Dit is, in termen van links van-relaties, alleen maar uit te drukken door één symbool (H) aan te nemen voor het geheel, dat de andere genoemde elementen vormen.

Deze weergave heeft echter als bezwaar dat een Pv als zodanig herkenbaar moet blijven in verband met de V-second transformatie-operatie^1., die Pv's uit hun basispositie achter in de ‘clause’ op de tweede plaats van de zin zet (bij ja/nee-vragen na een eerste constituent, zeg Q, die later wordt gedeleerd). Anders geformuleerd: op één niveau van de beschrijving moet Pv als zodanig gehonoreerd kunnen worden, op een ander niveau echter ‘genegeerd’ (nl. inzoverre het niet meer is dan een deel van H). Dat komt neer op ‘dubbellezen’ van de met H aangeduide reeksen: enerzijds als geheel, anderzijds in onderdelen.

Wanneer we erin zouden slagen een procedure aan te geven die dit verantwoordt, zou deze tevens gebruikt kunnen worden om de feiten die blijkens G1 en G2 in termen van links van-relaties onverenigbaar zijn, met elkaar in verband te brengen. Immers, H gedraagt zich ten opzichte van Inf = St (zie onder, blz. 105) verschillend al naar gelang van zijn ‘vulling’: met Pv alleen of met één of meer Inf's, al dan niet vergezeld van een Pv. Een procedure die ‘dubbellezen’ van H mogelijk maakt, kan dit volgordeverschil funderen. Ik meen dat er een dergelijke procedure is, nl. een reeksopbouw in fasen. Deze wil ik hieronder schetsen.

Uitgangspunt is de volgende reeks:

G3
X → PC → St → Y

1. Deze operatie is nodig omdat de plaats van persoonsvormen in andere dan afhankelijke zinnen moeilijk in termen van links van-relaties kan worden beschreven: zinnen als

(i)

besteedt Piet het werk uit

(ii)

(dat) Piet het werk uitbesteedt

zijn niet te beschrijven zonder gelijktijdig aan te nemen X → Y en Y → X, hetgeen gezien de eigen aard van de links van-relatie strijdige beweringen zijn.

[p. 105]

Deze reeks verantwoordt groepen als

(4)	(Piet denkt erover, het werk) uit (te) besteden
(5)	(toen Piet het werk) uitbesteedde

maar biedt geen aanknopingspunt voor de V-second-operatie. De redenering kan niet zijn, dat een optreden van uitsluitend St dit element als Pv karakteriseert, aangezien graph G3 ook geldt voor beknopte bijzinnen, getuige (4). Er moet dus worden aangegeven, wat de persoonsvorm is. Dat kan bijvoorbeeld door de volgende weergave:

G4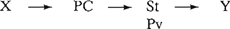

Hiermee wordt aangeduid dat besteedde in (5) als stamdrager weliswaar een vaste plaats heeft achter in de zin, maar als Pv zich leent voor de V-second-operatie. Er is dus sprake van gelijkheid in volgorde van Pv en St. Dit noteer ik als Pv = St.

Eenzelfde element Pv kan ook voorkomen buiten dit directe verband met St. Indien St het enige andere verbale element is, kan de distributie ervan als volgt worden weergegeven:

G5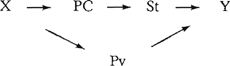

Voorbeelden hiervan zijn (1)a-f.

Verder is het mogelijk, dat Pv samenvalt met het eerste van een reeks hulpwerkwoorden, zoals bijvoorbeeld in

(6)	a (dat ik Piet het werk wel eens) uit zou willen zien besteden b (dat ik Piet het werk wel eens) zou willen zien uit besteden

(vgl. Bakker 1977: 379). Deze reeks (H) gedraagt zich als één element, waarin ook de Pv een vaste plaats heeft. Op grond van een gegeven bepalingsverhouding kan men de interne volgorde van de onderdelen van H bepalen. Deze stand van zaken is eveneens aan te geven door een = relatie te stellen tussen Pv en H: Pv = H. Zoals (6) illustreert, moet H vóór St staan als de hoofdwerkwoordsstam in een infinitief is vervat (Inf = St), anders is dat niet nodig, vgl. (1) h-j. Door de volgende twee graphs wordt dit geïllustreerd:

[p. 106]

G6



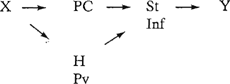G7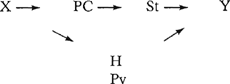

De graphs G4 t/m G7 zijn gebaseerd op:

de links van-relaties:

(7)	a X → PC b PC → St c St → Y d X → H e H → Y f H → Inf

de gelijkheidsrelaties:

(8)	a Pv = St b Pv = H c Inf = St

Als H → Inf van toepassing is, blijft H → Y gelden, maar volgt nu tevens uit de ‘nieuwe’ relaties H → Inf, Inf = St en uit St → Y. Hetzelfde geldt voor de relatie X → St, die volgt uit X → H, Pv = H, H → Inf en Inf = St, zoals men kan aflezen aan G1 hieronder. Wanneer H → Inf van toepassing is, dàt wordt bepaald door aanbod van volgorde-elementen (in willekeurige volgorde).

Het bovenstaande kan aldus worden samengevat. Op basis van de links van-relaties als weergegeven in

G1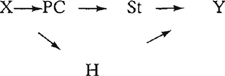

en de onder (7, 8) gegeven regels zijn te construeren:

1.	G4 door toevoeging van Pv aan St;
2.	G6 en G7 door toevoeging van Pv aan H (G7 is dan te beschrijven als het geval, waarbij Pv de enige vulling van H is);
3.	G6 door toevoeging van Inf aan St.

[p. 107]

Gebruikmakend van hetzelfde toevoegingsprincipe kunnen we Z (= zelfstandig werkwoord) toevoegen aan St (≠ Pv) en aldus een aanknopingspunt bieden voor Topicalisatie van St in de vorm van Inf of Vd van het zelfstandig werkwoord.^2. Daarmee kunnen uitgesloten worden zinnen als

(9)	*Geworden is hij ziek
(10)	*Worden zal hij ziek

Een zin als:

(11)	(dat hij ziek) zou hebben kunnen worden

kan dus gerepresenteerd worden als

G8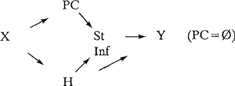

In de volgende graph is, onder eliminatie van het terzake van (11) overbodige PC, de daaraan verbonden relaties X → PC en PC → St, alsmede van H → Y, een structuur aangegeven (die dus uitsluitend geldt voor (11)):

G9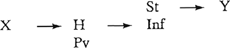

Hoewel eenzijdig, illustreert deze graph goed waar het om gaat: de elementen H Pv en St Inf hebben ieder twee aspecten, die relevant zijn voor de volgorde. Deze kunnen beschreven worden met behulp van additionele links van-relaties en invoering van de = relatie, welke laatste reeds gemotiveerd is met betrekking tot V-second en Topicalisatie. Het is deze veelheid van volgorde-aspecten in sommige elementen, die ons noopte uitgaande van een basisschema in termen van links van-relaties elementen en bijbehorende links van-relaties toe te voegen door middel van = relaties.

Iets dergelijks hoop ik te zijner tijd te kunnen laten zien voor Whelementen, onderwerp, meewerkend voorwerp en lijdend voorwerp, waarmee dan het bewijs geleverd zal zijn, dat hetzelfde verschijnsel zich ook in een geheel ander gebied van de ‘clause’ voordoet.

Deze bijdrage aan de oplossing van ‘woordgroepproblemen’ zij collega Van den Berg, die als een der eersten de beschrijving van woordgroepen aanvatte, in erkentelijkheid opgedragen.

2. Voor Topicalisatie geldt dezelfde argumentatie als in noot 1 voor V-second gegeven.

[p. 108]

Literatuur

Bakker, D.M. (1977)

‘De links-van-relatie in werkwoordsgroepen’, Spektator 6 nr. 7/8, 378-380.