Appels en peren / wiskunde en psychologie

Gebundelde opstellen

[p. 90]

7. Meten vanuit wiskundig standpunt

Het begin van meten

Getal, maat, gewicht en geld hebben vanouds veel met elkaar te maken. Desalniettemin gaat het meten ten dele aan het tellen vooraf. Je kunt tal van voorwerpen meten, eer je iets van getallen afweet.

‘Piet is groter dan Jan’ - dat kun je nagaan door ze met de achterhoofden tegen elkaar te plaatsen, met een latje op de kruinen, en te kijken naar welke kant het latje afloopt.

‘Piet is zwaarder dan Jan’ - laat ze maar op de wip gaan zitten.

‘Piet spreekt met een diepere stem dan Jan’ - dat kun je horen.

‘Van Amsterdam naar Arnhem is het verder dan naar Utrecht’ - nogal duidelijk, want Utrecht ligt ertussen.

Je hoeft de lengten, de gewichten, de toonhoogten, de afstanden niet altijd in getallen uit te drukken om te weten te komen wie groter, zwaarder, dieper is. Wie is het sterkste, wie kan het hardst lopen, wie kan het mooiste zingen - vanouds zijn er wedstrijden om rangordes van atleten, hardlopers, zangers te bepalen. Ook zonder stopwatch en andere moderne uitvindingen. Wat was de koudste winter, de heetste zomer sinds mensenheugenis - dit wisten ze ook zonder thermometer vast te stellen.

Het meest primitieve meten is een bepalen van volgorde. Neem zo'n ordebegrip, bijvoorbeeld ‘zwaarder dan’, of preciezer

... zwaarder dan...

waar bij de twee keer drie stippeltjes twee voorwerpen dienen te worden ingevuld. Of zo'n uitspraak waar is ga je met een weegschaal ook zonder gewichten na: A in de ene, B in de andere schaal en dan kijken naar welke kant het uitslaat.

Als

noch A zwaarder dan B, noch B zwaarder dan A,

beslis je

A even zwaar als B,

waar je ook voor mag zeggen

B even zwaar als A.

Om niet zoveel te hoeven schrijven, schrijven we maar kort:

A ∼ B

en in plaats van A zwaarder dan C:

A > C.

We merken enkele wetmatigheden op:

Als A > B	Als A > B	Als A ∼ B	Als A ∼ B
en B > C	en B ∼ C	en B > C	en B ∼ C
dan A > C	dan A > C	dan A < C	dan A ∼ C

[p. 91]

Als	A ∼ B
dan	B ∼ A
Altijd	A ∼ A

Je mag > ook lezen als ‘rent harder dan’, ‘is voedzamer dan’, ‘is slimmer dan’. De wetten van zopas blijven dan nog steeds juist.

Zoek meer voorbeelden! Mag je > ook lezen als ‘is neef van’, ‘is jarig ná’?

Een mooi voorbeeld is ook de hardheidsschaal. Je leest dan A > B als ‘A ritst B’. Het hardste is diamant. Met diamant kun je alles ritsen.

Schaal van Mohs
1. talk }	{ met de nagel
2. gips }	{ te krassen
3. calciet }	{ gemakkelijk met
4. fluoriet }	{ mes te krassen
5. apatiet }	{ moeilijk met mes
6. veldspaat }	{ te krassen
7. kwarts }	{ niet meer met
8. topaas }	{ vijl te krassen
9. korund }	{ maar geven kras
10. diamant }	{ op glas

Een edelsteen nu moet minstens de hardheid 7 hebben om niet door het overal liggende stof dat voor een groot deel uit zand d.w.z. kwarts bestaat, te worden geschuurd en dof gemaakt. Wel worden mineralen uit de kwartsgroep in grote hoeveelheden als sieraad gebruikt wegens hun mooie kleuren - ze worden speciaal in Idar-Oberstein vervaardigd - maar men noemt ze dan liever geen edelstenen, maar sier- of kleurstenen (Duits Schmucksteine). De vroegere naam van ‘half-edelsteen’ voor kwarts, wordt door de edelsteenhandel bewust niet meer gebruikt: men vindt de ongunstige klank ‘half’ te kort doen aan het fraaie uiterlijk van deze stenen!

Met het ∼-teken (even zwaar als) kun je (gewichts) klassen vormen. Je stopt alles wat even zwaar is in een klasse. Je kunt dan ook de klassen met elkaar vergelijken. Als A zwaarder is dan B, dan is elk voorwerp in de klasse van A zwaarder dan elk voorwerp in de klasse van B. In zo'n gewichtsklasse kun je een standaardgewicht kiezen. Een set gewichten bij een weegschaal geeft voor bepaalde gewichtsklassen standaardgewichten. Typisch is ook weer de hardheidsschaal; het is een schaal van standaardstoffen; van een nieuwe stof probeer je wat hij ritst en waardoor hij wordt geritst.

De gewichtsklassen vormen, wat men noemt een geordende verzameling. Ze laten zich als het ware op een rij zetten, zeg naar toenemende zwaarte van de leden.

Meten en getal

Hoe krijgt het getal nu vat op het meten? Men is er niet tevreden mee te weten wie van die A, B, C de zwaardere is. B is bijvoorbeeld maar eventjes zwaarder dan A, terwijl C heel veel zwaarder is dan B. Hoe meet je zoiets?

[p. 92]

Hierbij moet naast vergelijken volgens, zeg maar, gewichten een andere operatie meedoen, het ‘samenstellen’.

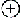
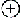
Jan is zwaarder dan Piet, maar als Lies nog bij Piet op de wip gaat zitten, zijn ze samen even zwaar als Jan. Ik heb Piet en Lies ‘samengesteld’ tot iets dat even zwaar is als Jan. Ik zeg ‘samenstellen’ en niet optellen. Optellen doe je met getallen. ‘Piet + Lies’ lijkt nergens op, maar omdat ik voor het samenstellen een teken moet hebben, gebruik ik maar eventjes als symbool, dus Jan ∼ Piet Lies.

Het kan ook gebeuren dat Jan even zwaar is als twee Pieten. Wat bedoel je hiermee? Al heb je er maar één, je gaat je een Piet* verschaffen, die even zwaar als Piet is en je constateert dat

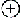
Jan ∼ Piet Piet*.

Jan heet dan dubbel zo zwaar als Piet.

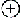
Net zo gaat het met dubbel zo lang en dubbel zo ver. Maar hoe zou het zijn met ‘A zingt dubbel zo mooi als B’? Je kunt misschien wel een B* vinden, die precies zo mooi zingt als B, maar hoe stel je B en B* volgens hun zangkunst samen? Moet je ze gelijktijdig of achtereenvolgens laten zingen, om de zangkunst van het koppel B B* met die van A alleen te vergelijken? Met ‘dubbel zo slim’ valt het misschien nog mee. Je laat A, B en B* een uur lang sommetjes rekenen en als A net zoveel klaarspeelt als B en B* samen, is hij even slim als zij, dus dubbel zo slim als elk afzonderlijk.

Of bent u het hiermee niet eens? ‘Dubbel zo helder’ - kan dit?

Ja, als je een blad papier op dezelfde afstand met één of twee gelijksoortige kaarsen verlicht wordt het dubbel zo helder.

Maar je moet met zo iets voorzichtig zijn. Als je dubbel zo hard muziek wilt maken, kom je er niet door dubbel zoveel mensen te laten zingen.

We begonnen met het grove meten van ‘A is zwaarder, langer, slimmer dan B’, ‘A is even zwaar, even lang, even slim als B’. We komen nu tot het verfijnde meten, waarbij het gewicht, de lengte, de slimheid van A in die van B numeriek wordt uitgedrukt. ‘Beter één vogel in de hand dan tien in de lucht’ (in welk opzicht beter?), één vrouw is duizend mannen te erg (in welk opzicht?). Voor het kunnen uitdrukken van het gewicht enzovoort van A in dat van B zijn twee dingen vereist: je moet dingen kunnen vergelijken of ze even zwaar enzovoort zijn en je moet ze kunnen samenstellen. Dan pas kun je zeggen A is zo zwaar, lang, slim als een aantal B's.

Er was eens een volksstam, die ruilhandel pleegde en als volgt rekende:

1 slaaf is evenveel waard als 3 slavinnen plus 1 ezel
1 slavin is evenveel waard als 2 stieren plus 1 schaap
1 stier is evenveel waard als 2 koeien
2 koeien zijn evenveel waard als 5 ezels
1 ezel is evenveel waard als 4 schapen

[p. 93]

Toen kwam er iemand op een idee: laten we alles in schapen uitdrukken. Een schaap was dus de wettelijke waarde-eenheid in deze economie. Dat kost zoveel schapen - zei de man die een huis wilde verkopen; zij kost zoveel schapen - zei de vader met een huwbare dochter.

Je noemt zoiets betalen in natura. Dit systeem werd afgelost door het betalen in klinkende munt. Als waarde-eenheid koos je een zekere hoeveelheid koper of zilver of goud.

Hetzelfde doe je altijd bij het numeriek meten. Je kiest een maateenheid: pond, voet, kilogram, duim, el, meter, schepel, mud, liter, dag, jaar, seconde, stuiver, duit, dollar, enzovoort. Je zorgt er verder voor dat je die eenheid voldoende kunt reproduceren, om te meten grootheden in de eenheden uit te drukken. Op de liniaal vind je vergelijkbare eenheden al afgetekend en samengesteld, maar als je een grotere afstand moet meten, stel je hem als het ware samen uit afstanden die je direct met de meetlat hebt uitgezet. Als je iets weegt, vergelijk je het met een samenstel van een aantal standaardgewichten. Weeg je met een unster, waar je een schaal afleest, dan komt het wegen als het ware op een afstand meten neer: hoe ver slaat de wijzer uit? En net zo is het bij het tijdmeten met de klok.

Als je maateenheden hebt ingevoerd, vergelijk je alles via die maateenheden - je meet met één maat. Als A 60 kg weegt en B 20 kg, weet je dat A drie keer zo zwaar is als B. Bovendien weet je: als B 20 kg weegt en C 40 kg, dan weegt het samenstel van B en C (we noemden het ook B C) 20 kg + 40 kg en dat is 60 kg.

Is dat goed, 20 kg + 40 kg? Mag ik gewichten optellen of alleen maar getallen? Is dat niet zo iets als Jan = Piet + Lies?

Wel, 20 kg betekent niet 20 afzonderlijke kilogramgewichten. 20 afzonderlijke kilogramgewichten is een samengesteld voorwerp waarvan ik toevallig precies weet dat het 20 kg weegt. Mijn koffer is ook zo'n voorwerp en weegt misschien ook 20 kg.

20 kg is - los van zijn feitelijke realisering - een rekenbegrip, waarmee ik rekenoperaties uitvoer. In de natuurkunde noemt men zo iets ook grootheden en werkt er rekenkundig mee. Je drukt gegeven grootheden numeriek in zekere eenheden uit; het is een groot gemak dat je aan die maatgetallen kunt zien of ze even groot zijn, wie groter is en hoeveel keer zo groot hij is; bovendien vind je het maatgetal van een samengesteld voorwerp door de maatgetallen van de delen op te tellen.

Bij al die bewerkingen doet de maateenheid er niet toe. Als A 20 kg weegt en B 40 kg, dan blijft B dubbel zo zwaar als je de maateenheid van kg in ons verandert en het gewicht van A B is hetzelfde of je het nu in kg of in ons uitdrukt.

Bewerkingen

Kun je met grootheden nu onbeperkt alle bewerkingen uitvoeren?

[p. 94]

20 kg + 100 m zul je zeker niet toelaten (als je wilt zeggen dat een draad 20 kg zwaar is en 100 m lang, hoor je dat in elk geval niet zo te zeggen). Je kunt wel iets dat 20 kg zwaar is met iets samenstellen dat 100 m lang is, maar van het samenstel wil je dan toch óf de zwaarte óf de lengte weten (of allebei).

Kun je nog andere bewerkingen op verschillendsoortige grootheden loslaten?

Het meest bekende is het delen van afstand door tijd. 100 meter in 15 seconden afgelegd, dat is 100/15 meter per seconde. Je noemt dat ook de snelheid.

Als je

in de tijd t
de weg w

aflegt, dan is

w/t de snelheid.

Hier zijn t en w bepaald niet maar getallen. De tijd 15 bestaat niet; een maateenheid is onmisbaar. Het is bijvoorbeeld 15 s of 15 h; de weg 100 bestaat niet; het is bijvoorbeeld 100 m of 100 km.

Naar gelang van die twee gevallen is de snelheid

100 m/15 s

of

100 km/15 h

(Het eerste een hardloper, maar geen wereldrecord; het tweede een flinke tippelaar.)

Je kunt de uitdrukkingen vereenvoudigen:

100 m/15 s = 6/⅔ m/s
100 km/15 h = 6⅔ km/h

en je leest die maatbepaling ook als meter per seconde, kilometer per uur. Soms geeft men de voorkeur aan m s^-1, km h^-1, dus sec^-1 in plaats van 1/s, h^-1 in plaats van 1/h.

Met m en km meet je afstanden,
met s en h meet je tijden,
met m/s en km/h meet je snelheden.

Als je op een oppervlakte van 10 m² een kracht van 500 kgf uitoefent, dan krijg je een druk van

500 kgf/10 m²

en dat is

50 kgf/m²

dus een druk van 50 kgf per vierkante meter. Is dat veel?

Boven elke vierkante centimeter staat een luchtzuil, die boven de hoogste bergen uitgaat en al wordt die lucht boven steeds ijler, toch oefent het gewicht van de lucht op een oppervlakte van 1 cm² een kracht uit van 1 kgf. De luchtdruk is dus 1 kgf/cm² = 10 000 kgf/m².

[p. 95]

Een vierkante meter, wat is dat? Het is het prettige van ons matenstelsel, dat alle maten uit een klein aantal fundamentele maten zijn opgebouwd. Om oppervlakte en inhouden te meten ga je op de lengtematen terug. Een rechthoek met zijden a en b heeft de oppervlakte a · b. Ja..., maar is dat een wet of een afspraak? Ten dele het een, ten dele het ander. Neem een rechthoek van zeg 3 eenheden lang en 2 eenheden breed (figuur 7.1). Je kunt hem opdelen in 3 · 2 vierkanten, waarvan de zijde de eenheid is. Dat is een wet. De afspraak is dat je uit de

figuur 7.1

eenheid van lengtemeting een eenheid van oppervlaktemeting maakt, te weten het vierkant met als zijde de lengte eenheid. Dat is dan voor een vierkant met zijde 1 cm de vierkante cm, oftewel cm², voor een vierkant met zijde 1 m de vierkante m, oftewel m².

Analoog is het met de inhoudsmeting. Je werkt dan met als eenheid de kubieke cm of cm³, dat is de inhoud van een kubus met ribbe 1 cm of de kubieke meter, of m³, de inhoud van een kubus van rubbe 1 m. Op die manier wordt dan de oppervlakte van een rechthoek met zijden 3 cm en 2 cm:

3 cm · 2 cm = 3 · 2 cm²,

de inhoud van een plaat van 4 cm lang, 3 cm breed, 2 cm hoog:

4 cm · 3 cm · 2 cm = 4 · 3 · 2 cm³.

Het kost even veel arbeid om een gewicht van 50 kgf 30 m hoog te tillen of 25 kgf 60 m hoog.

Je noemt de grootheid waar het hier om gaat: arbeid.

Het halve gewicht dubbel zo hoog tillen kost evenveel arbeid. Je berekent de arbeid daarom als produkt van de vereiste kracht (het op te tillen gewicht) en de vereiste hoogte. Om 50 kgf 30 m hoog te tillen is een arbeid nodig van

50 kgf · 30 m = 50 · 30 kgf m = 1500 kgf m

25 kgf 60 m hoog vereist dezelfde arbeid. Hoe vlug de motor het klaar speelt om de 50 kgf 30 m hoog te tillen hangt af van zijn (arbeids) vermogen. Om 50 kgf 30 m hoog te tillen in 10 seconden is een arbeidsvermogen vereist van

50 kgf · 30 m/10 s = 150 kgf m s^-1.

De gewone eenheid van arbeidsvermogen is 1 watt, ongeveer gelijk aan 1/10 kgf m s^-1, of het duizendvoud ervan, de kilowatt.

Zet je een toestel met een vermogen van 2 kilowatt 3 uur aan de gang, dan verbruikt het

2 kilowatt · 3 uur = 6 kilowattuur.

Je kunt nagaan wat dit volgens het elektriciteitstarief kost.

[p. 96]

Nieuwe grootheden

Uit de oorspronkelijke grootheden lengte, gewicht, tijd kun je door vermenigvuldigen en delen nieuwe grootheden vormen en door dezelfde bewerkingen krijg je maateenheden voor de nieuwe grootheden.

Wat gebeurt er nu als je van maateenheid veranderd, m door km of cm, kg door g, sec door h vervangt, enzovoort.

Wel,

1 km = 1000 m,
1 h = 3600 s.

1 km per uur is dus dezelfde snelheid als 1000 m per 3600 s, dus

1 km/h	= 1000 m/3600 s
	= 0,28 m/s
	= 28 cm/s

of met ons voorbeeld van zoëven:

100 km/15 h	= 100 000 m/54 000 s
	= 1,88 m/s

Een druk van 500 kg op 10 m² is

500 kgf/10 m^2	= 500 000 gf/100 000 cm^2
	= 5 gf/cm^2

dus 5 gram per vierkante centimeter.

Een rechthoek van 3 m bij 2 m heeft een oppervlakte van

3 m · 2 m = 6 m²

of

30 dm · 20 dm = 600 dm²

of

300 cm · 200 cm = 60 000 cm²

en analoog met de inhoudsmaten.

Je kunt dus gemakkelijk van de ene maateenheid naar de andere overstappen. Waarvoor bezig je nu bij dezelfde grooteenheid verschillende maateenheden? Wel, als ik de lengte van een kamer in meters wil meten, zal het misschien niet precies uitkomen, zeg 5 m en nog iets.

Dat iets is te klein voor een meter en ik ga het in dm meten, zeg 6 dm en nog iets. En dat nog iets blijkt 3 cm te zijn en nog iets. Zo kan ik doorgaan met de maateenheid telkens weer onder te verdelen. Wil ik dan toch alles in meters uitdrukken, dan moet het met kommagetallen geschieden, zoals

5,63... m.

[p. 97]

Terug- en vooruitblik

Het was erg concreet. Laten we de vragen even concreet stellen.

1.	Wat heeft meten met tellen te maken?
2.	Kun je ‘toonhoogte’ meten door een telprocedure?
3.	Ken je voorbeelden van metingen waarbij het subjectieve element niet geheel te elimineren is?
4.	Welke grootheden kun je echt ‘objectief’ meten?
5.	Hoe tracht men leerlingenprestaties zo objectief mogelijk te meten?
6.	Vertel iets over het verband tussen getal, maat, meten, geld en gewicht.
7.	Wat zijn de karakteristieke eigenschappen van de orde ‘is zwaarder dan’?
8.	Noem ze ook voor de orderelatie ‘is knapper dan’.
9.	Hoe kun je theoretisch tot een verzameling standaardafstanden komen?
10.	Bedenk een zinvolle achtergrond voor Westertoren + Martinitoren > Domtoren.
11.	In welk opzicht kun je het invoeren van geld als betaalmiddel vergelijken met het meten van gewichten?
12.	Rekenoperaties zijn bedoeld voor getallen.
	Je kunt wel zeggen 5 × 3 = 15, maar niet δ δ δ δ δ + δ δ = 7.
	Waarom is de uitspraak 5 km + 3 km = 8 km nu toch juist vanuit wiskundig standpunt en 5 liter water = 5 kg niet?
13.	En hoe zit dat met 5 km × 3 km?
14.	Kun je iets vertellen bij de operatie 50 km/1 uur?

Nu een geheel andere visie. Minder wiskunde en meer kinderen in het beeld.