|
| |
| |
| |
Werken aan onderwijs: op weg
Kort of lang - aan mathematische produktiviteit komt een einde. Meestal eerder
dan aan het leven en vaak veel eerder. Waarom? Om individueel uiteenlopende
redenen. Je kunt de ontwikkeling van de wetenschap niet bijhouden, of je houdt
hem bij en dat vreemde gedachtengoed verstikt je eigen produktiviteit. Of het is
gewoon een - vroeg - ouderdomsverschijnsel. Of - zoek het maar uit. Er zijn
nogal wat collega's, die zich dan - bij gebrek aan een andere hobby - met
wiskunde als uitgangspunt op filosofie, geschiedenis of onderwijszaken
toeleggen. Zo eenvoudig was het bij mij toch niet. Ik heb me heel vroeg voor
deze randgebieden van de wiskunde geïnteresseerd. Ik heb nog vrij
lang wiskunde geproduceerd, zij het dan dank zij een extreme versmalling van
mijn breder werkgebied. Mocht dit voortgezette werk ooit opgepakt worden - ik
vertrouw erop - dan zal ik er toch niet meer getuige van zijn.
De weg in mijn werken aan onderwijs is niet eenvoudig te reconstrueren. Wat
uiterlijkheden aangaat natuurlijk wel, maar ik heb weinig zin in de paperassen
te duiken die ik ook eerst nog uit de kluis van het Mathematisch Instituut zou
moeten halen. Nee, wat ik zou willen nagaan is: wanneer en hoe ben ik op een
bepaald idee gekomen dat ten slotte in mijn werk werd ingelijfd?
Ik heb vroegtijdig les gegeven - privé-lessen dan - volgens het
Dagboek op zijn minst al met dertien jaar. Slechte vermoedelijk. Mijn hele leven
ben ik een slecht leermeester geweest. Ik was me er ook van bewust en om er het
beste van te maken ben ik al vroeg over onderwijs gaan nadenken. Aan mijn
leraren heb ik me niet gespiegeld, evenmin als, wat opvoeding betreft, aan mijn
opvoeders. Of wel, maar dan in de zin van: het moest beter. Aan | |
| |
mezelf heb ik me aldoor gespiegeld. Ook: het moest beter. Een inzicht om anderen
voor te houden. Je deed zelf steeds je best, al was het beroerd, maar dat kon je
niet helpen. Je hebt van die geboren onderwijzers en opvoeders, die er niet over
na hoeven te denken en het je dus ook niet kunnen vertellen hoe je het
klaarspeelt een goed onderwijzer en opvoeder te worden. Je kunt ze
wél gadeslaan.
Ik heb vanaf het begin van mijn verblijf in Nederland mijn kritiek op het
Nederlandse wiskunde-onderwijs niet onder stoelen en banken gestoken, al bleven
het onderonsjes. Ons, dat waren D. van Dantzig, mijn medeassistent bij L.E.J.
Brouwer, W. Hurewicz, maar ook een groepje studenten, waaronder bij voorbeeld
Johan de Iongh, Wim Bloemendal, Pierre van Hiele en Dieke Geldof (later Pierre's
echtgenote). Die kritiek betrof allereerst het inhoudelijk geheel verouderde
universitaire wiskunde-onderwijs, maar ook de onderwijsmethode. Zodra ik een
stuk voorkandidaats onderwijs in handen kreeg (in 1937 de analyse), heb ik
oefeningen naast de colleges ingevoerd en van begin af aan heb ik met Hurewicz
een colloquium voor kandidaten geleid. Maar wat me het meest schokte, was de
onnoemelijk lange studieduur in Nederland - sommige, van mijn studenten waren
ouder dan ik. Ikzelf had het wel ook niet zo vlug gedaan: zeven jaar, van de
eerste inschrijving tot de promotie, in Berlijn, met een semester tussendoor in
Parijs. Maar ik moest ook mijn hele studie zelf verdienen, hoofdzakelijk met
privé-lessen - spoedig ten dele ook als studentassistent. De oorzaak
van de lange Nederlandse studieduur was nogal duidelijk: de kleine patriarchale
universiteiten, waar elke hoogleraar zich met elke student bemoeide en wel in de
vorm van tentamens, over elk college afzonderlijk af te leggen - tentamens die
zich bij een aantal hooggeleerden plachten uit te strekken over een hele dag,
bij sommige zelfs over een hele week.
De nieuwe leerstof die ik invoerde was
‘Bourbaki-avant-la-lettre’ - goede stof, maar te hoog
gegrepen, hoewel door de oefeningen verzacht. Nee,
‘Bourbaki-avant-la-lettre’ - dat is weer overdreven. Het
was hoog gegrepen, maar toch wel overwogen didactisch. Niemand die me toen
hierbij terzijde stond. Ik | |
| |
was de eerste die moderne wiskunde in
Nederlandse collegezalen bracht en dan zijn fouten onvermijdelijk.
Tot de discussie omtrent de universiteit, die ten slotte leidde tot een nieuwe
Wet op het Hoger Onderwijs, heb ik ook het mijne bijgedragen. Hoofdschotel: een
geschrift van 73 getypte bladzijden, ‘Oude en nieuwe
universiteiten’ (niet gepubliceerd), maar brokjes van die
ideeën kwamen toch via lezingen en De Groene
Amsterdammer in het openbaar. In dat geschrift ontvouwde ik ook mijn
ideeën over universitair onderwijs, die - wat de wiskunde betreft -
culmineerden in het wiskunde-practicum. Geen oefeningen meer, maar een practicum
dat de colleges ten dele moest vervangen.
In Amsterdam kreeg ik nog eventjes de kans dat te realiseren. Toen ik in Utrecht
kwam, was er nauwelijks plaats en tijd voor colleges - terwijl de
wiskundeleerstoelen vacant waren, had de natuurkunde alles in beslag genomen. Na
een strijd die enkele jaren duurde, lukte het: practica met medewerking van
studentassistenten. Hoe het zich verder heeft ontwikkeld - ik bemoei me er al
lang niet meer mee. De mensen worstelen nu met heel andere problemen, waar je
geen weet van, geen kijk op hebt.
Iets anders dat ik heb neergeschreven en niet gepubliceerd - trouwens niet eens
voltooid - was een rekendidactiek. Het manuscript - 103 bladzijden folio getypt
en wat niet-getypte die zoek zijn - moet uit 1942 dateren. Ik heb toen - in de
oorlogsjaren - Didi en Thijs rekenen en lezen geleerd, en voor het
rekenonderwijs heb ik de hele literatuur die ik te pakken kon krijgen
bestudeerd; het boekje aantekeningen van de literatuurstudies is er nog. Ik zei
het al: het manuscript is niet voltooid - ik zou zelfs kunnen zeggen dat ik aan
de eigenlijke rekendidactiek niet ben toegekomen. Een zwak idee van wat die
eigenlijke ‘Rekendidactiek’ behelst zou hebben, geeft het
- eveneens niet gepubliceerde - manuscript van een lezing, ‘Opvoeding
tot denken’, die ik op de eerste conferentie van de Werkgemeenschap
voor Vernieuwing van Opvoeding en Onderwijs (wvo) na de
oorlog, in augustus 1945, op Rhederoord heb gehouden - nu, veertig jaar later,
houd ik er op een enkel fundamenteel punt - speciaal wat het leren van de
grondbewerkingen betreft - een andere mening | |
| |
op na. Aan de andere
kant, in het manuscript bladerend vind ik veel van mijn tegenwoordige
opvattingen terug. Soms tot mijn eigen verbazing. Ik beschouwde het toen bij
voorbeeld al als een averechts idee het klassikaal onderwijs te vervangen door
individueel onderwijs zoals de Montessorianen deden; ik had toen al mijn zinnen
gezet op onderwijs in kleine groepen; waarom weet ik niet, want het karakter van
de groep, het sociaal en eventueel heterogeen karakter, komt niet uit de verf.
Op mijn scepticisme ten aanzien van wat psychologie en algemene didactiek en
methodenleer tot de rekendidactiek konden bijdragen, hoef ik heden nog geen
fundamentele correctie aan te brengen, van het voordeel van de twijfel dat ik
toen nog aan de toetsontwikkeling wilde toekennen, is alleen de twijfel
overgebleven. In het meeste dat ik toen heb geschreven herken ik mezelf nu nog,
speciaal in het afwijzen van de ‘vormende’ waarde van
reken- en, impliciet, wiskunde-onderwijs; maar ik ben er vast van overtuigd dat
ik tien jaar eerder, toen ik het didactiek-colloquium leidde, ook al de wiskunde
als middel voor ‘leren denken’ afwees. Ik heb het
manuscript van 1942 geboeid herlezen, soms, zoals ik al zei, verbaasd dat ik dit
of dat toen al heb gezegd, soms teleurgesteld door het gevoel: wat heb je er
eigenlijk bijgeleerd? Het valt mee: ik heb allereerst geleerd gedachten aan te
scherpen, maar dat heeft dan ook weer veel te maken met nieuwe stromingen in het
wiskunde-onderwijs, die tegen mijn ideeën ingingen. In het manuscript
van 1942 keer ik me bij voorbeeld tegen degenen die in het onderwijs de
cognitieve ontwikkeling willen vervangen door een cognitieve volgorde,
preciezer: door die cognitieve volgorde die uit hun eigen (logische) analyse
voortvloeit. Het lijkt of ik toen vooruitliep op mijn kritiek op Piaget (die
trouwens toen nog nauwelijks iets ter zake had gepubliceerd), maar ook op mijn
kritiek op New Math. De voorstanders van New Math waren nog radicaler dan
degenen die ik in mijn manuscript van 1942 bestreed. Ze stelden immers dat de
structuur der wiskunde - en dat was dan de door Bourbaki uitgelijnde - ook de
structuur van het onderwijs moest bepalen.
Het ene radicalisme lokt het andere uit. Zodoende schiep ik de term
‘antididactische inversie’, waarmee ik de neiging van de
| |
| |
wiskundige bedoelde in het schoonschrift zijn gedachtengangen
tegengesteld aan hun ontstaanswijze voor te stellen en liefst ook zijn onderwijs
zo in te richten. Maar deze aanscherping dateert uit de jaren voor of rond 1960
en heeft nog andere, wellicht diepere wortels dan alleen de reactie op New Math.
Ik bedoel de theorie van de niveaus in het leerproces, door de Van Hieles
geïnstigeerd, waarvan ik in 1942 nog geen flauw idee had.
Om mijn verhaal goed in te kaderen, moet ik nog veel verder teruggaan en dan tot
1924 - jaren voor ik in Nederland kwam - het soort annus mirabilis van de
wiskundedidactiek in Nederland om mee te beginnen. Drie gebeurtenissen, alle in
1924, markeren dit begin: van het Nieuw Tijdschrift voor
wiskunde, een opleidingssteun voor akte ki- en kv-aspiranten wordt een ‘Bijvoegsel’
afgezonderd, om te beletten dat het als gevolg van al die didactische en
historische bijdragen uit zijn voegen barstte; na een driejarige zwangerschap
werd de navelstreng met zijn moederorgaan zelfs doorgesneden, en met de naam Euclides, heeft de boreling - inmiddels officieel orgaan van
verenigingen voor wiskundeleraren - in 1985/86 de leeftijd van 61 jaar bereikt.
Het eerste bijvoegsel begint met een artikel van E.J. Dijksterhuis
‘Moet het meetkunde-onderwijs gewijzigd worden?’, een
kritiek op de bij Wolters in hetzelfde jaar 1924 verschenen brochure van Tatjana
Ehrenfest-Afanassjeva ‘Wat kan en moet het meetkunde-onderwijs aan
een niet-wiskundige geven?’, waarin Tatjana Ehrenfest had gepleit
voor een meetkundige propedeuse, voorafgaande aan een logisch en systematisch
(maar dan afgeslankt) meetkunde-onderwijs. De discussie Ehrenfest-Dijksterhuis
herlezend vraag ik me thans af: ‘Waar hebben ze zich toen druk om
gemaakt?’ Van wat toen meetkunde-onderwijs heette, rust immers het
stoffelijk overschot al zowat vijftien jaar vredig naast het geestelijk
overschot daar waar het door de Mammoetfanaten ter vergetelheid is besteld. Het
was wat je noemt het kind met het badwater weggooien, en al heb je er achteraf
spijt van, het is in oorzaak en gevolg een bij historici en sociologen bekend
verschijnsel: voor problemen waar je niet uitkomt is ‘alles of
niets’ een patentoplossing. Zij die hardnekkig
‘alles’ verdedigen, moeten met lede ogen | |
| |
uiteindelijk met ‘niets’ genoegen nemen. De meetkunde ging
eruit vanwege het didactisch onzindelijke badwater, waarin twaalfjarigen werden
ondergedompeld om met haar kennis te maken, veel ‘luctor’
en weinig ‘emergo’. Wat kwam er in plaats van die
meetkunde? Didactisch nog onzindelijker badwater, maar dan zonder ook maar
één kind erin. Het is de oude tragiek van iets verdedigen
omdat het je lief en dierbaar is en om geen enkele andere reden dan dat het je
lief en dierbaar is, zonder je af te vragen of dit ook voor anderen een reden
kan zijn het zich te laten opdringen. Breek ik hier over anderen de staf? Ik zou
mezelf niet van die aanklacht vrij kunnen pleiten dat ik zelf in het verleden
deze neiging heb vertoond en ook nu nog vertoon. Hoofdstuk xvi van Mathematik als pädagogische Aufgabe,
met de titel ‘Der Fall der Geometrie’, waarin ik daarmee
afreken, heeft als eerste motto ‘Hochmut kommt vor dem
Fall’ - een spel met het woord. ‘Fall’ dat je
niet kunt vertalen. ‘Hoogmoed’ is zeker een wat krasse
term voor de mentaliteit die ik net schetste: het willen opdringen van wat men
als cultureel erfgoed beschouwt aan een jeugd, die er niet mee gediend is,
trouwens nooit gediend was: de ‘jeugd van tegenwoordig’
van weleer is net zo jeugd als die van heden.
Achteraf bekeken was ook Tatjana Ehrenfests poging, zoals ze bedoeld was,
vergeefs. Dat haar werk in ander opzicht vruchten heeft gedragen, staat op een
ander blaadje. Ook Tatjana Ehrenfest geloofde in een deductief systeem van de
meetkunde dat je de jeugd moest leren - misschien zelfs nog strakker dan het
toen gangbare - maar zij wilde die deducriviteit voorbereiden door een
propedeuse, een aanschouwelijke introductie. Van wat er aanschouwelijk in de
meetkunde te beleven en te leren valt, heeft ze blijk gegeven in haar Übungensammlung zu einer geometrischen
Propädeuse van 1931 - een meesterwerk als je er meer in ziet
dan een propedeuse, dat wil zeggen: meer dan een voorbereiding op een
systematisch deductief systeem van de meetkunde. Ik moet toegeven dat het
inzicht in die meerwaarde ook bij mij langzaam is gerijpt. Het deductief systeem
van de meetkunde - het ideaal voor de eliteschool, was een schijnvertoning,
zelfs voor de elite-leerlingen, en voor de massaschool nog minder dan dat. Eind
ja- | |
| |
ren zestig slaagde ik erin te formuleren wat mij als
oplossing voor ogen zweefde: deductiviteit ja, maar dan lokaal, door de leerling
te overzien, niet globaal, als systeem door stokpaardjes-ruiters verzonnen.
Ik ben al weer een heel eind op de historie vooruitgelopen. Tussen 1924 en het
eind van de jaren vijftig ligt immers dezelfde drempel als die waarvan ik naar
aanleiding van het manuscript van 1942 sprak.
Twee evenementen uit 1924 hebben we al gesignaleerd: de conceptie van Euclides en de brochure van Tatjana Ehrenfest. Het derde was
het verschijnen van het ‘Ontwerp van een leerplan voor het onderwijs
in wiskunde, mechanica en kosmographie op de hb-scholen met
vijfjarige cursus’ (zie Euclides 2, 113-139) van de
inspectoriale commissie H.J.E. Beth. Hoe men toen over wiskunde-onderwijs dacht,
blijkt uit de zinsnede:
‘Hoofddoel van het wiskunde-onderwijs is het bijdragen tot geestelijke
vorming en ontwikkeling; nevendoel het aanbrengen van nuttige
kennis.’
Men - daarmee bedoel ik de toonaangevende kliek, waarvan inderdaad H.J.E. Beth en
in de meest extreme mate H. Schogt representanten waren. De man in de klas die
die wiskunde op de hbs moest onderwijzen, heeft zeker niet zo
hooggestemde doelen op het oog gehad, en in feite zijn er soms in Euclides minder hooggestemde geluiden uit de praktijk te horen. Niet
alleen uit de praktijk. Alleen al de titel van Van Dantzig ‘Over de
maatschappelijke waarde van onderwijs in de wiskunde’ (Euclides 3, 156-196) getuigt van een heel andere mentaliteit, die
echter nauwelijks meetelde - wie wilde het zich ook laten aanleunen wiskunde om
haar maatschappelijke waarde te onderwijzen waar geestelijke vorming en
ontwikkeling als na te streven idealen golden?
Niettemin wist E.W. Beth dertig jaar later zijn vader nog te overtroeven (J.
Piaget et al., L'enseignement mathématique,
Neuchâtel 1955):
‘Le rôle de la formation mathématique dans
l'enseignement secondaire consiste presque exclusivement, me
paraît-il, à familiariser les élèves
avec la méthode déductive.’
| |
| |
Ik zei ‘niettemin’ om de tegenstelling tot Van Dantzig te
beklemtonen en die tot na-oorlogse ontwikkelingen die Van Dantzig in het gelijk
hebben gesteld. Aan de andere kant moet ik toegeven dat E.W. Beth niets anders
deed dan een traditie voortzetten, een traditie die straks in het onderwijzen
van een nog abstractere, nog deductievere wiskunde zou zegevieren om
uiteindelijk de smadelijkste nederlaag te lijden, maar ook dit is weer van een
latere datum: het tijdperk van New Math dat niet met de Spoetnik, maar al vroeg
in de jaren vijftig begint. Het lijkt ironie dat ik, die helemaal tegen deze
stroom zou oproeien, bij de Internationale Commissie voor Wiskunde Onderwijs
(icmi) als Nederlandse vertegenwoordiger E.W. Beths
opvolger werd. Ironie, maar ook niet veel meer dan dat. Ik was, ook later als
president, een vreemde eend in die bijt - maar dat is al weer vooruitlopen op de
geschiedenis.
Terug naar het hooggestemde wiskundeleerplan van de Commissie H.J.E. Beth, voor
de hbs, door Thorbecke geschapen als -burgerschool, maar toen al flink op weg naar de geleerdenschool waarvan het gymnasium de traditie zei voort te zetten.
Van de drie strengen die ik in 1924 liet beginnen, pak ik allereerst die van de
Commissie Beth weer op. Het leerplan ging de ijskast in, waar het ineens in 1937
door inspecteur Van Andel weer uit werd gehaald. ‘Historisch
gegroeid’ noemde Van Andel het (in de ijskast?). Was het als
proefballon bedoeld? Het is door de lerarenverenigingen geaccepteerd, toen
vaststond dat het - althans voorlopig - geen consequenties zou hebben voor de
examens. De oude examenregeling van 1929 bleef van kracht en dat betekende dat
er in de praktijk niet veel veranderde.
De geschiedenis nam echter een onverwachte keer. De vierde streng begon op 20
april 1936: de oprichting van de Wiskunde Werkgroep (ww) van
de wvo, zelf een jaar eerder opgericht, in het internationaal
verband van New Educational Fellowship, en nationaal met Kees Boeke als centrale
figuur.
Ook van deze start was ik geen ooggetuige. Naar wat er bij het gouden feest van
de wvo boven water is gekomen, valt er over het vooroorlogse
reilen en zeilen van de Wiskunde Werkgroep niet veel te memoreren. Wansink moet
er een rol in heb- | |
| |
ben gespeeld, en ook Tatjana Ehrenfest en
wellicht de Van Hieles.
Suus was al voor de oorlog lid van de wvo of nee, alleen maar
lezeres van Vernieuwing. Na de oorlog werd ze lid van de
Centrale Werkgroep (het bestuur), waarvan Kees Boeke de ziel en de bezieler was
- ik stond nooit zo nabij Kees Boeke als Suus. Ik leerde hem wel eerder kennen,
op Rhederoord (de Steeg) waar van 11 tot 14 augustus 1945 de wvo haar eerste naoorlogse conferentie hield. In het hoofdstuk
‘Reizen’ heb ik er al over gerept. Een van de conferenties
waar je je opsluit in een aparte wereld, die - dat hoop je - straks zal
uitbarsten en dan die daarbuiten zal overspoelen. Ik maak er in deze context
gewag van omdat ik voor die conferentie het manuscript ‘Opvoeding tot
denken’ schreef en er een nabeschouwing ‘Struggle for
life’ aan wijdde, die ik allebei nog met plezier heb herlezen.
De Wiskunde Werkgroep van de wvo hervatte haar werkzaamheden
na de oorlog op 15 juni 1946. Ik was er toen ook nog niet bij. Ik weet niet wie
mij erbij heeft gehaald, Minnaert die er lid van was en de bibliotheek van zijn
sterrenwacht graag voor bijeenkomsten beschikbaar stelde, of Hermen Jacobs,
secretaris, die toen zijn door de oorlog onderbroken wiskundestudie in Utrecht
aan het afronden was - ik was daar op 4 oktober 1946 tot hoogleraar benoemd.
Mogelijk was de eerste bijeenkomst die ik bijwoonde die op 11 januari 1947 in
het Montessorilyceum in de De Lairessestraat in Amsterdam (ik woonde toen nog in
die stad), maar ik herinner me er niets van, evenmin als van de bijeenkomsten
daarna, in Bussum, Amsterdam, op de sterrenwacht, bij Tatjana Ehrenfest, in de
A.v. Dijkstraat in Amsterdam, enzovoort - om de beurt.
Wat me nog ten volle heugt is het eerste openbare optreden van de ww in het Maarten Maartensz Huis in Doorn, het weekeinde van 13 en 14
november 1948, de eerste in een lange rij najaarsconferenties, in
conferentieoorden en jeugdherbergen. Na zijn opening, begin 1951, was vanaf 3
februari het Mathematisch Instituut (toen Boothstraat 17 in Utrecht) de plaats
van de maandelijkse bijeenkomsten. Al in 1950 had ik het voorzitterschap van de
ww van J.R. Janssen overgenomen, toen en later gesteund
| |
| |
door Hermen Jacobs als secretaris. De aanvankelijk slordig
gestencilde verslagen van de bijeenkomsten kregen vanaf 1953 een netter
uiterlijk. Niets, vergeleken bij het tijdschrift Euclides,
maar wie in de toenmalige jaargangen van Euclides bladert, zal
de overheersende invloed van de ww niet ontgaan. Het meest
sprekende voorbeeld, in Euclides 28: ‘Het
wiskunde-programma van het vhmo - een ontwerp van de Wiskunde
Werkgroep van de wvo’, waaraan over de jaren
1948-1952 door ruim veertig leden was gewerkt. De strekking van dit programma
was lijnrecht tegengesteld aan die van de Commissie Beth: geen hooggestemde
doelen, wel begrip voor de dienende functie van de wiskunde, radicale snoei van
wildgroei en inhoudelijke modernisering. De strekking was trouwens ook
tegengesteld aan wat kort daarna als New Math het wiskunde-onderwijs zou
bedreigen. De verenigingen voor wiskundeleraren speelden er gauw op in: in 1955
werd een nieuw leerplan in de geest van het ww ontwerp
officieel afgekondigd. Helaas, het was geen lang leven beschoren. Met de
invoering van de Mammoetwet (1968) moest er ook een nieuw leerplan komen. Het
kwam er, helaas, maar hierover later.
Waarom vertel ik dat allemaal, in een hoofdstuk ‘Werken aan onderwijs:
op weg’ (mijn weg uiteraard)? Ergens - ik weet niet meer waar - heb
ik de ww mijn hogeschool van de wiskunde-onderwijskunde
genoemd - een hogeschool waarvan ik bij het zilveren feest van de ww vanuit Yale op de band zei dat men daar van elkaar leerde. Onder
alle gemeenschappen die zich met het wiskunde-onderwijs onledig hielden, heeft
tot het iowo toe geen me zo geboeid als de ww. Het kader van mijn doen en denken in wiskunde-onderwijs was het jaar
1942, misschien al tien jaar eerder gevormd, maar dit kader moest nog gevuld
worden, de ideeën nog aangescherpt. De ww was voor
mij en anderen het milieu van wiskundig-didactische bewustwording - voor het
gouden feest van de wvo heb ik kortgeleden in Vernieuwing een artikel geschreven over de ww,
waarin ik deze historische rol van de ww heb uiteengezet.
Voor mijzelf kwam er echter nog iets bij, maar dat moet ik voor later bewaren.
In mijn rectoraatsjaar 1963/64 gaf ik heel wat voorzitterschappen op, misschien
ook dat van de ww. Wanneer ik voor het | |
| |
laatst
een bijeenkomst van de werkgroep heb bijgewoond kan ik niet vaststellen. In 1974
is de ww opgeheven.
Ben ik de Wiskunde Werkgroep ontrouw geworden? Ik heb zowat vijftien jaar op wat
ik mijn hogeschool van de wiskunde-onderwijskunde noemde, gezeten, maar van elke
school moet je een keer af. Ik ging wat ik daar geleerd had uitdragen in wijder
kringen. Welke kringen - het zal de minder betrokken lezer weinig interesseren
dat in details te vernemen, maar ik wil ze toch iets van de sfeer laten proeven.
Het begint weer met wat historie: we hebben in Nederland een Wiskundig
Genootschap, na het Hamburgse het oudste ter wereld; in 1979 heeft het zijn
tweede eeuwfeest gevierd. Het is ooit opgericht door een groep mensen die
belangstelling voor de wiskunde had of van de wiskunde profiteerde, zoals land-,
scheeps- en vatenmeters en opleiders van kapiteins en stuurlieden. Met de
opbloei van wiskunde op school gingen de wiskundeleraren de kern van het
genootschap vormen - het bestuur bestond in onze eeuw echter meestal uit
hoogleraren, met een verzekeringswiskundige als penningmeester en een leraar als
secretaris. Tegenwoordig zullen er nog maar weinig leraren lid van zijn
(bovendien is er een grote vereniging van wiskundeleraren). Het ledenbestand van
het Wiskundig Genootschap telt nu wiskundigen van universiteiten en het
bedrijfsleven; op de colloquia en symposia en het jaarlijkse congres wordt
wiskunde voorgedragen, al is er op dat congres wel eens een sectie voor
‘wiskunde-onderwijs’.
Elk genootschap heeft zijn commissies en van het Wiskundig Genootschap is de
Nederlandse Onderwijs Commissie voor Wiskunde (nocw) er een.
Het bijvoeglijk naamwoord ‘Nederlands’ duidt op een
internationaal verband, en inderdaad, de nocw geldt als
subcommissie van de imuk (Internationale
Mathematik-Unterrichts Kommission) = ciem (Commission
Internationale pour l'Enseignement Mathématique) = icmi (International Commission on Mathematical Instruction). Dat ik de
Duitse afkorting hier voorop heb geplaatst, heeft historische redenen. De
stuwende kracht en de eerste president (1908) van de imuk was
de - terecht of ten onrechte - vermaarde Duitse wiskundige Felix | |
| |
Klein, haast uniek in de wiskundewereld door zijn belangstelling voor
wiskunde-onderwijs op school.
Uiteraard staat het Wiskundig Genootschap zelf ook in een internationaal verband.
Er is een International Mathematical Union (imu), met als
hoofdtaak om de vier jaren een internationaal mathematisch congres op touw te
zetten (in 1954 vond het plaats in Amsterdam). Het Wiskundig Genootschap stuurt
uiteraard zijn vertegenwoordigers naar de imu. Deze imu heeft na de Tweede Wereldoorlog de imuk-ciem-icmi als eigen Commissie geadopteerd.
President en ‘Members at large’ worden door het imu-bestuur benoemd; de landelijke
‘subcommissies’ zoals de nocw sturen er
vertegenwoordigers naartoe.
Hierboven had ik het over een Werkgroep, de ww van de wvo - trouwens in de wvo noemde ook het
bestuur zich werkgroep, de ‘Centrale Werkgroep’. Er is een
hemelsbreed verschil tussen commissies en werkgroepen, dit wil zeggen tussen hun
uitersten, want er zijn ook overgangen - een brede scala. Ik heb in mijn leven
in heel wat raden en commissies gezeten, maar waar ik de kans schoon zag heb ik
zo'n lichaam een beetje als werkgroep laten functioneren of zich werkgroepen
laten assumeren - geen enkele had de daadkracht van de ww van
de wvo, maar toch.
Wat doet een commissie voor het wiskunde-onderwijs? Zich met de buitenkant van
het onderwijs bezighouden. En een werkgroep? Met de binnenkant. De buitenkant,
dat zijn de soorten onderwijs met hun doelstellingen, programma's, examens,
bevoegdheden, alles waarvoor je de vereiste kennis met enquêtes
vanuit en studies achter het bureau kunt verwerven. Heel nuttig soms, maar niet
mijn cup of tea. Dat wil niet zeggen dat werkgroepen per se beter zijn. Het
criterium is dat ze deugdelijk werk afleveren. Maar dat is dan ook het zere
punt, vergeleken met de commissies: wie beslist wat deugdelijk is?
Naast de tegenstelling tussen commissie en werkgroep is er nog een andere: die
tussen vak en onderwijs - in casu wiskunde en wiskunde-onderwijs. Een
tegenstelling in het persoonlijke vlak: aan de ene kant de
wetenschapsbeoefenaar, bevreesd - trouwens soms ook terecht - voor de
‘pedagogums’ en ‘pedagooche- | |
| |
laars’ die zijn dierbare vak zouden kunnen besmetten, aan de andere
kant de wiskundige op school die - jammer genoeg - te vaak bang is voor de
wenkbrauwen fronsende wiskundebeoefenaar. Ik bevond me in het schaars begroeide
tussenveld: een wiskundige met een zekere - soms wat overdreven -
wetenschappelijke reputatie die (ik heb lang geaarzeld hoe ik het moest zeggen)
tevens op de hogeschool van de wiskunde-onderwijskunde zat. Een enfant terrible
- zowel nationaal als internationaal - waar ze blijkbaar toch niet omheen
konden, zoals straks zal blijken. Of hoopten ze dat ik al rijzende mijn wilde
haren zou kwijtraken?
In 1954 volgde ik E.W. Beth op als voorzitter van de nocw -
wat een tegenstelling als u zich de hierboven geciteerde Franse uitlating van
Beth herinnert! Ik had al eerder op het internationale toneel gestaan, maar nu
kwam ik er officieel, als Nederlands vertegenwoordiger bij de icmi. Bij mijn eerste optreden in de icmi (3 juli
1955), in aansluiting op een colloquium in Genève, behaalde ik ook
mijn eerste succes.
Een van de belangrijkste taken van de icmi was het
voorbereiden van de sectie Onderwijs van het eerstvolgende Internationaal
Mathematisch Congres. Ik kreeg iets gedaan: een van de drie thema's werd
‘Initiation into Geometry’. Ik had alle drie die thema's
naar de binnenkant van het onderwijs willen wentelen; hoewel dit niet lukte,
hebben wij in Nederland aan alle drie thema's meegewerkt: voor elk van die drie
stelde de nocw een werkgroep in. De rapporten van de
werkgroepen vertaalde ik in het Engels om ze gedrukt, op het Congres in
Edinburgh in 1958, aan de sectie Onderwijs aan te bieden. Ikzelf rapporteerde in
Edinburgh over de nationale rapporten bij het thema ‘Initiation into
Geometry’.
‘Inleiding in de meetkunde’, het thema waarmee Tatjana
Ehrenfest-Afanassjeva in 1924 de aftrap in de Nederlandse
wiskunde-onderwijskunde deed, waar de ww van de wvo zich over had gebogen en waarover in 1957 de Van Hieles vanuit
verschillende invalshoeken bij Langeveld en mij waren gepromoveerd - het was een
kolfje naar mijn hand. Het Nederlandse rapport ontleent zijn grote historische
betekenis aan de bijdrage van de Van Hieles - feitelijk door mij uit hun diverse
publikaties samengesteld. | |
| |
De bijdrage was de eerste internationaal
toegankelijke uiteenzetting van hun niveautheorie, waarover straks.
Ik klom om de vier jaar een trede op de icmi-ladder: 1958
Member at large, 1962 lid van het Executieve Comitee, 1966 president, 1970
‘oud-president’, 1974 icmi
vertegenwoordiger in het icsu Committee on Science Teaching.
Het klinkt misschien onbescheiden: tot op heden ben ik de enige icmi-president geweest, met hart en hoofd voor wiskunde op school -
Behnke, de eerste onder wie ik in de icmi zat, en Hassler
Whitney, de tegenwoordige, niet te na gesproken, die had en heeft er zeker hart
voor. Het is een wonder dat de leiders van de International Mathematical Union
me zo hoog lieten klimmen, benauwd als ze zijn voor hun dierbare vak en voor de
pretenties van onderwijskunde. Botsingen waren er geregeld: de oprichting van
Educational Studies in Mathematics, het eerste
internationale tijdschrift voor wiskunde-onderwijs, nadat l'Enseignement Mathématique geheel op wiskunde sec was
overgeschakeld; het eerste internationale congres voor wiskunde-onderwijs, in
Lyon in 1969, waarvan men vreesde dat het als concurrent het Internationaal
Mathematisch Congres schade zou berokkenen, terwijl het alleen maar de sectie
onderwijs van dat congres zou overvleugelen. Ik vrees dat ik al in te veel
details ben getreden - ik heb Geoffrey Howson toen hij er voor zijn artikel over
75 jaar icmi in Educational Studies in
Mathematics 15 om vroeg, een uitvoerige documentaire brief over mijn
internationale onderwijsactiviteiten geschreven.
In het nationale veld heeft het zelfs nog langer geduurd voor ik mijn reputatie
van enfant terrible kwijtraakte. De doorbraak kwam, jammer genoeg, te laat, maar
was steviger en duurzamer dan elders ter wereld. De doorbraak - nee, dat is niet
de juiste term. Het was veeleer: een dam opwerpen tegen de internationale
bandjir van New Math. En om dat te vertellen moet ik weer terug naar het
internationale veld.
In onze eeuw heeft de wiskunde - net als vele andere wetenschappen - een
geweldige groei in breedte, diepte en hoogte te zien gegeven. Maar er was meer:
een aloude neiging om de wiskunde telkens weer te reorganiseren, en dat ook weer
met wiskundige middelen, verstevigde zich tot een bewust beleefde | |
| |
stormachtige trend. Een Franse groep - Bourbaki - gaf er gestalte aan: een
systeem van de wiskunde, vanaf de meest algemene begrippen, afdalende naar de
meer en meer gespecialiseerde - een lange weg die in feite nooit werd afgelegd,
maar toch als systeem indrukwekkend van architectuur. Indrukwekkend, maar
onvoltooid, want onder het reorganiseren groeit de wiskunde tussen je vingers
door. Niettemin, qua structuur een schoonheid, die vooral die mensen fascineerde
die alleen maar die structuur zagen en nauwelijks wisten waartoe die structuur
diende. In de jaren vijftig was het nog maar een kleine schare die erdoor
gegrepen werd: volgens dit fraaie systeem moest wiskunde op school worden
onderwezen.
Gezaghebbende wiskundigen demonstreerden het voor onderwijskundigen die er zich
aan vergaapten al had geen van hen een flauw idee waar deze begrippen in de
wiskunde toe dienden. Het was een absurde bevlieging wiskunde vanuit dit
perspectief op school te onderwijzen - ik heb deze dwaze geestesgesteldheid toen
niet au sérieux genomen en dat was misschien de grootste taxatiefout
die ik in mijn leven heb gemaakt.
Het begon dus niet pas met de Spoetnik-shock. Het begon al vroeg in de jaren
vijftig. Zelfs Piaget, die er niets van begreep behalve dat het woord
‘structuur’ hem aansprak, hadden ze ertoe weten over te
halen. Met Piagets naam op het reclamebord meenden ze zich verzekerd van de
steun van de psychologie. Wat psychologie! Wiskunde kent een logische orde en
voor wie wiskunde onderwijst is de verleiding groot de psychologische, de
onderwijskundige orde aan de logische op te offeren. Ik heb mijn best gedaan dit
te vermijden en in mijn ‘Fragment Rekendidactiek’ van
1942, zo niet al vroeger, heb ik er anderen voor willen waarschuwen. Maar wat
zag ik nu gebeuren? Een ten top gedreven logische orde, een systematiek van de
wiskunde als geheel - zo zou de wiskunde moeten worden onderwezen. En dat met de
zegen van een psycholoog, een epistemologisch psycholoog die het erop hield dat
de wiskunde zich bij het individu volgens ‘epistemische’
lijnen onwikkelde - dat wel. Dank zij de spoetnik-shock zagen ze hun kans
schoon. De schoolwiskunde was zo ver achtergebleven bij de wiskundige wetenschap
dat er schoon schip | |
| |
moest worden gemaakt. De oeso (toen nog oeeo), de organisatie voor economische
samenwerking, pakte de zaak op.
Wat had de oeso met onderwijs te maken? Het was het Bureau
voor wetenschappelijk en technisch personeel waaronder de vraag naar nieuw
wiskunde-onderwijs ressorteerde. Ik trachtte de oeso-vertegenwoordiger die me kwam opzoeken om te praten: niet
‘Enseignement de mathématiques modernes’, maar
‘Enseignement moderne des mathématiques’ zoals
de titel van een van mijn opstellen luidt. Het mocht niet baten: de oeso ging in zee met vooraanstaande wiskundigen zonder enige
relatie met het wiskunde-onderwijs.
Zodoende kwam er eind 1959 het fameuze Royaumont Seminar. Ik liet me er niet
naartoe delegeren omdat ik schoon genoeg had van dit soort conferenties. Het
bleek een kardinale fout. Royaumont was niet zo maar een conferentie, regeringen
hadden er vertegenwoordigers naartoe gestuurd - een conferentie met gezag
bekleed. Had ik, als ik er geweest was, de besluiten van Royaumont tegen kunnen
houden? Ik had in elk geval nog harder kunnen schreeuwen dan mijn vermaarde
vriend Dieudonné. Achteraf bekeken was het niet alleen een fout dat
ik niet naar Royaumont ging, maar het ging dwars tegen mijn gewoonte in mij niet
afzijdig te houden maar mee te werken om bij te sturen, een gewoonte die ik bij
voorbeeld later in de cmlw getrouw naleefde.
Had ik de stroom van New Math die dank zij Royaumont als een bandjir door zou
razen, kunnen tegenhouden? Welnu, het had geen bandjir hoeven te worden. Hoe dan
ook, New Math, in Royaumont gelegaliseerd, trok zijn verwoestend spoor
wereldwijd door het wiskunde-onderwijs. In Royaumont, door mij onderschat, begon
de wereldwijde zegetocht van New Math, die op een smadelijke nederlaag zou
uitlopen. Alleen Nederland bleef enigszins gespaard.
Op het appel van de oeso antwoordde Nederland met het
instellen, op 12 juni 1961, van de Commissie Modernisering Leerplan Wiskunde
(cmlw). Op 19 juli 1961 werd de Commissie
geïnstalleerd. Ik zat toen op het eind van mijn Sabbathical Year in
usa. Mijn eerste reactie op de cmlw-plannen was negatief (25 | |
| |
augustus 1961). Toch heb ik -
voor zover men het me toestond - loyaal meegewerkt. Trouwens, ik had niets
anders kunnen doen - de tijd was nog niet rijp voor mijn denkbeelden. Ik was nog
steeds het enfant terrible. Ik mocht er wel voor spek en bonen meedoen.
Maar laat ik eerlijk zijn: wij - ik incluis - werden overrompeld. Met de
feitelijke invoering van de Mammoetwet moesten de nieuwe leerplannen wiskunde op
tafel liggen. Auteursgroepen die in het buitenland hun licht hadden opgestoken,
waren ons te vlug af geweest. Voor de leerplannen er kwamen, waren ze al
geïnterpreteerd. Een beetje New Math, niet veel, maar toch
té veel en in elk geval gespeend van elke relatie met de realiteit,
van elk inzicht in de dienende taak van de wiskunde. Had het anders gekund?
Misschien wel, als we enkele jaren respijt hadden gehad. De spoed van toen heeft
ons vijftien tot twintig jaar gekost. Het nieuwe bleek praktisch van begin af
aan mis. Heel duidelijk was dat in de bovenbouw, maar je mocht het niet hardop
zeggen om de lerarengemeenschap niet nodeloos ongerust te maken. Wat aan de
bovenbouw schortte, is nu, drie lustra later, ten dele gerepareerd. Wat er op
mavo-niveau gebeurde was veel erger - ik moet bekennen
dat ook ik het toen maar bij benadering besefte. Wie kon weten dat het mavo niet zomaar een voortzetting van het mulo zou zijn, maar voor jaren en jaren de ruggegraat van ons voortgezet
onderwijs? Met een mavo- of lbo-getuigschrift op zak is de leerling getrakteerd geweest op een soort
wiskunde dat voor zijn verdere ontwikkeling waardeloos is - sterker: dat op
niets lijkt dat men ergens ter wereld echt wiskunde mag noemen, al is het elders
in de wereld nog erger. Als de voortekenen niet bedriegen, gaat straks ook de
onderbouw van het voortgezet onderwijs in de steigers. Te lang is de discussie
vertroebeld door politieke strijd: voor en tegen de middenschool.
We faalden toen omdat we meenden dat we naast het verrichten van ons gewone werk
ook nog het onderwijs konden vernieuwen. Voor het evenzeer bedreigde
basisonderwijs waren we inmiddels beter toegerust: een aantal professionele
medewerkers die de op vernieuwing beluste uitgevers tegenhielden met het
dreigende vooruitzicht op een nieuw leerplan dat geheim werd | |
| |
gehouden. We kregen respijt en we kregen het iowo als een
instituut waar je rekening mee moest houden. In het basisonderwijs zijn ons de
rampen bespaard gebleven die andere landen hebben geteisterd. Maar al waren er
geen rampen - het kostte en kost tijd om tegenstanders te overwinnen.
Ik ben heel ver afgedwaald. Ik heb willen excuseren waarom ik van de Hogeschool
van de Wiskunde Werkgroep van de wvo afscheid nam en daarbij
ben ik mijn werken aan onderwijs als een weg, een lijdensweg, door commissies en
conferenties, gaan beschrijven in plaats van mijn weg van groeiend inzicht.
Om de draad weer op te pakken moet ik herhalen waar ik begon: met het inzicht dat
de logische orde van de wiskunde niet bepalend is voor de psychologische en
onderwijskundige - een inzicht waar je hard voor moest vechten om het bij
anderen op te roepen en dat ik steeds maar harder moest confronteren met wat de
New Math-vernieuwers nastreefden. Maar waar haalde ik die psychologische, die
onderwijskundige orde vandaan? Uit het onderwijs dat er slecht aan voldeed? Uit
proefnemingen die ver boven mijn mogelijkheden uitstegen? Hoe kon ik mij en
anderen overtuigen van wat die orde behelsde? Niet dat die vraag mij kwelde,
maar zolang ik die vraag niet kon beantwoorden, bleef het bij algemeenheden.
Het antwoord - een theoretisch antwoord - kwam toen de Van Hieles aan hun
proefschrift werkten, dus ongeveer in 1955/ 56: de niveaus van de Van Hieles.
Pierre claimt - zeker terecht - de niveautheorie voor zichzelf, maar het was het
meetkunde-onderwijs van Dieke waar hij de - door haar intuïtief
gebezigde - niveaus ontdekte en uitkristalliseerde. Wat ik van de Van Hieles
leerde heb ik op mijn eigen wijze verwerkt - zo gaat het nu eenmaal.
Het ordecriterium is niet een van de inhouden. Het is het niveauverschil en dit
niveauverschil is theoretisch te achterhalen, of als je wilt, door een
gedachtenexperiment, als je maar het leren als een door de leerling
geïnstigeerd en door de leraar gestuurd proces beschouwt.
Discovery learning, ontdekkend leren, was een tijd lang zo'n slogan. Ik heb er
nooit in geloofd. Soms werd ik er kregel van. | |
| |
In mijn boek van
1973, Mathematik als pädagogische Aufgabe = Mathematics as an Educational Task, spreek ik over
‘Nacherfindung unter Führung’,
‘guided reïnvention’, dus: geleide
heruitvinding. Maar het idee is veel ouder. In een artikel van me in Rekenschap (1957) is het al zodanig afgerond dat het veel
verder in het verleden moet wortelen. In míjn verleden, bedoel ik,
want in dat van de mensheid kun je het - ik ben er zeker van - heel ver terug
volgen. Ik vermoed dat het idee zich in de Wiskunde Werkgroep van de wvo heeft gevormd - de Van Hieles, vooral Dieke, gaven er in
hun onderwijs immers gestalte aan. Of gaat het terug tot Tatjana Ehrenfests Übungensammlung?
Wat je tevoren moet kunnen of weten om dit of dat uit te vinden kun je wel in het
gedachtenexperiment achterhalen, maar hoe zet je de gedachtenexperimenten op?
Waar laat je je door leiden?
Heruitvinding is een typisch wiskunde-onderwijskundig idee. Niemand zou eraan
denken leerlingen ook maar de eenvoudigste natuur- en scheikunde te laten
heruitvinden, laat staan de aardrijkskunde en geschiedenis. Maar met eenvoudige
wiskunde lukt het soms zelfs zonder leiding, met eenvoudige reken- en meetkunde.
Het kind gaat de wereld om zich heen ‘mathematiseren’.
Mathematiseren - weer zo'n term. Ik weet niet van wie die afkomstig is, maar met
betrekking tot het onderwijs was ik mogelijk de eerste die hem bezigde, wellicht
ook in onze Wiskunde Werkgroep-discussies.
Mathematiseren is in eerste aanleg het ordenen van de werkelijkheid met
mathematische middelen, expres voor dit doel geschapen - de ruimtelijke
verschijnselen meetkundig en hetgeen we de revue laten passeren, rekenkundig.
Dat is dan de eerste wiskunde, nieuw verworven, de door onszelf uitgevonden
werkelijkheid der figuren en getallen en die is wederom te ordenen met
mathematische middelen, meetkundige, rekenkundige, algebraïsche,
logische, om opnieuw wiskunde te scheppen - een voortgaand proces in een
uitdijende werkelijkheid.
Waar komt de term ‘mathematiseren’ vandaan? Er ging een
andere term aan vooraf: axiomatiseren. Axiomatische meetkunde kende je vanouds,
maar zeker vanaf het begin van deze eeuw | |
| |
werd axiomatiseren een
bewust geoefende en als zodanig onderkende wiskundige activiteit: een als
vanzelf gegroeid veld van begrippen en uitspraken omtrent die begrippen zodanig
ordenen, dat je enkele voorop stelt om de andere eruit af te leiden - een manier
van wiskundig orde scheppen in de wiskunde. Maar van wat wij mathematiseren
zouden gaan noemen, was het axiomatiseren dan de hoogste (of op
één na hoogste) trap, de meest geraffineerde.
Mathematiseren begint al lager, vlak bij de tastbare of primitief beleefde
werkelijkheid.
Meetkunde werd traditioneel onderwezen door met axioma's te beginnen, althans te
doen alsof - dat was je aan de Oudheid verschuldigd. Tatjana Ehrenfest was een
van de eersten die inzag dat dit fout was en die er iets - een propedeuse - aan
vooraf wilde laten gaan. Iets vooraf, als voorspel, maar niet als bron. Geleide
herontdekking zou betekenen dat je niet axioma's, maar het axiomatiseren
onderwijst, niet de nieuwe orde, maar het ordenen, niet mathematica als een
gereed produkt, maar het mathematiseren, en dan vanaf het laagste niveau,
voortschrijdend zover als leerlingen dit bij kunnen en willen houden - hier
openbaren zich de individuele verschillen. ‘Progressief
mathematiseren’ zeg je tegenwoordig - een verhelderende aanvulling.
Het mathematiseringsproces waar de Van Hieles zich vooral mee bezighielden, was
dat van de meetkunde, preciezer gezegd: ze waren de eersten die het meetkundig
leerproces als proces van mathematiseren interpreteerden (al gebruikten ze de
term niet, evenmin als de term heruitvinding). Zodoende ontdekte Pierre in het
onderwijs, zoals Dieke het beschreef, de niveaus waarvan ik eerder sprak. Ik
pakte die ontdekking op - wellicht het belangrijkste element in mijn eigen
wiskunde-onderwijskundig leerproces.
Het is uit mijn boek van 1973 meer algemeen bekend, maar, zoals veel in dit boek,
het is slechts een herdruk of vertaling van tijdschriftartikelen uit het begin
van de jaren zestig.
Zoals ik Van Hieles meetkundige niveaus op de wiskunde als geheel toegepast
interpreteerde, wordt wat op het lager niveau wiskundig handelen was, onderwerp
van onderzoek op het hogere - op het hogere wordt de wiskundige activiteit van
het lager | |
| |
niveau object van reflectie: door op je wiskundig
handelen te reflecteren schep je nieuwe wiskunde - de eerste ontdekker
én de lerende herontdekker.
In mijn wiskunde-onderwijskundig leerproces is de kennis van Van Hieles niveaus
cruciaal geweest omdat ik daarbij de reflectie als niveauverhogende activiteit
herkende: bewustmaking van je onbewust kennen, weten, handelen, het erop
reflecteren - hoe weet je dat, waarom doe je dat - en ten slotte het verwoorden
van het resultaat van je analyse, soms door beproefde taalmiddelen een nieuwe
functie toe te kennen, soms door nieuwe te scheppen. Dit is de manier waarop een
produktief wiskundige - althans voor zover ik mijn ervaringen mag generaliseren
- te werk gaat en het is dezelfde activiteit die je de lerende moet toestaan, of
liefst bij hem zou moeten stimuleren. Dit is dan ook wat ik steeds meer in mijn
praktijk - observeren van en onderwijs aan kinderen en volwassenen - ben gaan
beoefenen. Geleidend observeren van leerprocessen, en dan niet alleen
wiskundige: ‘Hoe weet je dat, waarom doe je dat?’
‘Zomaar, het is zo, ik zie het zo, ik voel het aan.’ En
dan ga je insisteren, desnoods hulp biedend; je tracht het onbewuste bewust te
maken, tot onderwerp van reflectie - de verwoording ervan is iets dat bij jonge
kinderen nogal eens hulp vereist. Maar het blijft niet tot de wiskunde beperkt
en in het geheel van mijn voorbeeldobservaties is de wiskunde maar een beperkt
deel. Toch licht ik het graag toe met een wiskundig voorbeeld; de diagonalen van
een parallellogram, die elkaar middendoor delen.

Je ziet het zo dat ze dat doen, en zelfs wie het wiskundig kan bewijzen, wist het
al lang voor zijn wiskundelessen begonnen. Maar hoe wist hij dat? Een echt
antwoord hierop is al wiskunde, maar ook aan het antwoord ‘ik zie het
zo’ heb ik hele meetkundelessen vastgeknoopt.
| |
| |
Om van mijn wiskunde-onderwijskunde de historie te schrijven, heb ik veel in oude
artikelen en manuscripten gebladerd. En dan zie je heel wat ideeën
zich vroeg aftekenen, nog impliciet, tussen de regels en andere gedachtengangen
door. Op een keer maak je je zo'n idee bewust, misschien nog onvoldoende
geverbaliseerd. In de discussie - zeker in de Wiskunde Werkgroep, en later
vooral in die met iowo-medewerkers, individueel en
groepsgewijs - wordt dit aangescherpt; mijn strijd tegen New Math heeft er veel
toe bijgedragen. Zo zie je in mijn wiskunde-onderwijskundig leerproces dezelfde
trekken als de in het wiskunde uitvinden en heruitvinden gesignaleerde.
Ik was vroegtijdig een voorstander van de kleine leergroep -
‘heterogeen’ zei ik er toen niet bij. Waarom? Wat had ik
geobserveerd - echt of in het gedachtenexperiment - om dit te rechtvaardigen?
Samen met de cruciale betekenis van de reflectie ging ik dit vatten. Reflecteren
op je eentje is moeilijk. Je moet het leren en dat doe je door samen, met elkaar
als groep, te reflecteren - ik heb trouwens net al de rol geschetst die
discussies, individueel en in een groep, in mijn eigen ontwikkeling hebben
gespeeld. Trouwens: reflecteren is ook je in tweeën (of
drieën) splitsen, met je alter ego discussiëren. Waarom
heterogene leergroepen? Omdat je door de grotere distantie in de groep meer maar
ook geheel andere dingen, al reflecterend, naar boven kunt halen.
Dat wiskunde in de realiteit wordt beoefend en ook zo moet worden onderwezen, is
een denkbeeld dat zich in mijn ontwikkeling steeds verder ontplooide, mede door
het besef van de cruciale betekenis van de reflectie. Het is een uitdijende
realiteit en hetgeen die realiteit in ‘abstracte’ sferen
doet uitdijen, is de telkens herhaalde reflectie. Wiskunde wordt in de realiteit
beoefend, mede om van de weeromstuit die realiteit - dus niet alleen door
uitdijen - te beïnvloeden en te veranderen. ‘Wiskunde
toepassen’ - noem je dat als het in de heel
‘concrete’ realiteit geschiedt. Voor het merendeel van wie
op school rekenen-wiskunde leren is dit toepassen zelfs het rationale van het
wiskunde-onderwijs. Je kunt wiskunde ook uit weetgierigheid of voor je plezier
leren of om het vak met hetzelfde oogmerk te beoefenen, je kunt het leren om het
zelf te onderwijzen - indirecte toepassin- | |
| |
gen die ik hier niet
bedoel. Er bestaat een vak ‘toegepaste wiskunde’. Ik heb
vroegtijdig aangevoeld dat het onderwijzen van toegepaste wiskunde niet de weg
is om wiskunde te doen leren toepassen, maar pas met de niveaus en de reflectie
werd me duidelijk waarom. Vervolgens, dus ook weer rond 1960, ben ik het
scherper en scherper gaan formuleren. Rekenen leer je in de realiteit, waar je
dingen - ook gedachte dingen - tellend en steeds maar handiger tellend
manipuleert, en de meesten leren dat simpele rekenen ook in simpele situaties
toepassen omdat ze er eerder via simpele situaties zijn ingestapt. Over het
simpele rekenen gesproken! Want bij de breuken, gewone of tientallige, is het
anders gesteld. Daarmee begin je misschien heel eventjes in de realiteit, maar
dan is het ook afgelopen, met als gevolg voor de meerderheid dat je de
breukoperaties, indien je die dan ooit leert, totaal niet kunt toepassen. En zo
gaat het door in het traditioneel wiskunde-onderwijs: wiskunde leren om achteraf
toe te passen - een didactisch averechtse procedure, waarmee de meesten niet
gediend zijn, ook al zijn die toepassingen - die ze toch niet aankunnen - dan
het rationale van hun wiskunde-leren. Ook hier weer het euvel van het instappen
op een niveau waar je eerst naar toe hoort te groeien. Hoe het moet, heb ik zo
geformuleerd en dan steeds scherper: de realiteit waar je wiskunde in wilt
toepassen moet je allereerst als bron gebruiken voor die wiskunde die je erin
wilt toepassen. Geen toepassen achteraf - ja dit ook - maar allereerst het
gebied van toepassing verkennen, zelf mathematiseren, onbewust, bewust en
reflecterend. Zo ontstaat in de realiteit de wiskunde die je
daar wilt toepassen. Zo was historisch de gang van zaken, de weg die je ook de
lerende moet toestaan om te bewandelen, stimulerend toestaan.
Let wel, niet één keer in de realiteit die je dan mag
vergeten, maar telkens weer heen en terug, en om dit te realiseren moet je
datgene waar je in de realiteit je oog op richt ‘rijk’
zijn, een rijke context of een paradigmatische situatie. Naar
onderwijs-paradigmata had ik wel meer uitgekeken, maar voor wat het paradigma
van mijn paradigma's zou worden, zou ik vrij nauwkeurig het ogenblik kunnen
bepalen waarop het mij te binnen schoot, zich aan mij opdrong - het was maart
1970, een belangrijke cesuur. | |
| |
Het is de vraag: Hoeveel
verschillende wegen zijn er van A over B naar C?
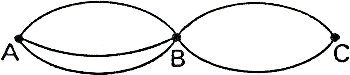
De vraag - en dus het antwoord - staat model voor een rist van vragen,
gelijksoortige, ingewikkeldere, als beginpunt van een groot stuk wiskunde, van
de onderbouw van de lagere school als je wilt tot heel hoog boven, een vaak door
mij beproefde weg.
Een rijk paradigma. Rijke contexten - ik weet niet wie op het iowo het eerst deze term heeft gebruikt. In elk geval stamt het idee uit
het concreet ontwikkelingswerk van het iowo en het zal
eventjes geduurd hebben voor het bewust gemaakt en verwoord werd - er is
inmiddels veel op gereflecteerd. Oorspronkelijk was het alleen maar
‘context’. ‘Rijk’ kwam erbij toen de
rijkdom zich onder het ontwikkelen manifesteerde.
Om de bronnen van wiskundige ideeën in de realiteit op te sporen heb
ik, misschien al vóór de niveau- en reflexie-theorie iets
in het oog gevat dat ik fenomenologie noemde. Niet het soort fenomenologie
waaraan door sommige filosofen ruchtbaarheid en beruchtheid is verleend, maar
veeleer lijkend op het soort dat de natuurkundige zo noemt; fenomenologie in de
zin van de fenomenen op te sporen die tot de wiskundige gedachte aanleiding
geven. Zeker sinds het begin van de jaren zestig heb ik dit woord herhaaldelijk
gebezigd. Ik heb zelfs voorbeelden van fenomenologie uitgewerkt om ze ten slotte
als Didactical Phenomenology of Mathematical Structures, mijn
laatste grote werk - in de jaren zeventig begonnen en niet afgemaakt - te
publiceren. Het is geen theorie van wiskunde-onderwijs, maar veeleer een (op
vele punten nog te weinig) gedetailleerde analyse van de bronnen van de wiskunde
in de realiteit. Uit didactisch perspectief dan en nuttig, naar ik meen, voor
wie de behoefte voelt met deze bronnen bij de ontwikkeling van
wiskunde-onderwijs rekening te houden.
In het voorafgaande heb ik een poging gedaan de bronnen van | |
| |
mijn
eigen wiskunde-onderwijskundige ideeën op te sporen. Ik heb geen
volledigheid willen betrachten. Is er na de geschetste ontwikkelingen nog iets
bijgekomen? Ik zou zeggen dat er nog haast dagelijks iets bijkomt - ik blijf nog
steeds leerprocessen observeren, van anderen en van mezelf. Ik slaag erin oude
ideeën te verfijnen en aan te scherpen, maar wat er fundamenteel
bijkomt, komt van anderen, door mij opgepakt en voor zover mogelijk verwerkt.
Trouwens, misschien is dat altijd zo geweest, al valt het me nu meer op, omdat
het nu veelal op papier en niet meer in stimulerende discussies op me afkomt.
Ik heb didactische ervaringen opgedaan en verwerkt, aanvankelijk in het
voortgezet onderwijs, later in het lager onderwijs en op de Pedagogische
Academie waar ik in de jaren zeventig een à twee keer per week lessen
bijwoonde, ervaringen uiteraard ook met mezelf en met medewerkers.
‘Op weg’ staat in de titel. Rechtlijnig? Ik zou zeggen, van
wel. Een aanmatigend antwoord? Ik heb geboft. Alwaar ik tegen een muur aankeek
ging ten langen leste een deur open. Een van eigen inzicht, maar meestal
andermans (zoals Van Hieles niveaus). Een weg die ik, om te beschrijven, in een
chaos heb moeten uittekenen.
Wel, om de chaos te vervolmaken, moet ik op het eind van die weg de maximes van
de aanvang tegenspreken. ‘Ich bin kein ausgeklügelt Buch,
ich bin ein Mensch mit seinem Widerspruch.’
Van meet af aan, voor zover ik me kan herinneren, heb ik de vormende waarde van
het wiskunde-onderwijs ontkend. Van het fragment
‘Rekendidactiek’ (1942) via mijn Rhederoordse lezing
‘Opvoeding tot denken’ (1945) tot mijn discussie met
Tatjana Ehrenfest (1951) deed ik dit in steeds krasser termen. Om haar eenvoud
zou wiskunde het meest aangewezen terrein zijn om goede denkgewoonten te kweken.
Ja, wiskundige denkgewoonten. Maar het is juist haar eenvoud -
resultaat van abstraherende vereenvoudiging - die voor velen in het onderwijs de
wiskunde het summum van moeilijkheid doet zijn. En die eenvoud is het ook die de
toepasbaarheid van de wiskunde elders - in deze allesbehalve eenvoudige wereld -
bemoeilijkt. Geen transfer, geen vormende waarde.
| |
| |
Nu, op het eind van de weg, sla ik de vormende waarde van het wiskunde-leren hoog
aan, geweldig hoog. Een strijdigheid? Ja en nee. Het komt erop aan wat je
wiskunde en wiskunde-onderwijs noemt. Ook die noties hebben op
die weg een wijziging ondergaan. De geïsoleerde, van de realiteit
hermetisch afgesloten wiskunde van toen - denk aan mijn citaten -, daar ging ik
tegenin, en des te harder naarmate de isolering, de afsluiting van de realiteit
in New Math tot de top werd gedreven. Geleidelijk kwam er een ander zicht op
wiskunde. Een wiskunde binnen de realiteit en dan niet alleen in die van de
ruimte, die ons de meetkunde heeft beschoren, niet alleen in de povere van het
koopmans-rekenen, niet alleen op de grote hoogte van die wetenschappen die om
wiskunde vragen.
Geleidelijk, zei ik, maar toen kwam de doorbraak van het rijke paradigma en - dat
was de stuwende kracht van het iowo - van de rijke context.
Een rijkdom die alles overtrof wat ik me tevoren had kunnen verbeelden.
Wiskunde binnen de realiteit en daarom van immense vormende waarde, maar nog lang
niet geaccepteerd. Wiskunde hoort immers ‘clean’ te zijn
en context is ‘ruis’, beletsel voor clean onderwijs. Maar
de wereld is nu eenmaal ruis, gebruis, en dát te elimineren is ook
wiskunde: het mathematiseren van de realiteit.
‘Werken aan onderwijs - op weg’ staat boven dit hoofdstuk,
en ten slotte bleek het alleen wiskunde-onderwijs. Herhaaldelijk dacht ik aan
zijsprongen, maar zag ervan af om de chaos niet te vergroten, om het enigszins
overzichtelijk te houden. Ik heb me veel met onderwijs meer in het algemeen
bemoeid, maar nooit met onderwijs als leeg vat, door anderen te vullen, zoals
sommige psychologen en algemeen onderwijskundigen het opvatten, die in en door
het lawaai wanneer je op dat vat trommelt, de meeste zelfbevrediging scheppen en
de meeste aandacht trekken. Of veeleer: voor zover ik mij wel met zoiets heb
bemoeid, was het om onwetendheid, charlatanerie en boerenbedrog aan de kaak te
stellen.
Onderwijs is nog steeds onderwijs van iets - en voor mij was het overwegend dat
van wiskunde. Je kunt ervan abstraheren, en | |
| |
dat heb ik niet
versmaad, maar niet door het volle vat leeg te gieten en erop te trommelen.
Ik heb ook getrommeld, maar niet op lege vaten, ik heb de trom geroerd om voor
mijn ideeën te werven, in het onderwijs en anderszins. Ja dat is het,
ik ben een tamboer geweest, ik heb de trom geroerd om mensen wakker te maken.
Daar schiet me iets te binnen - een anekdote. Ik heb vroegtijdig geijverd voor
pedagogisch-didactische vorming van de toekomstige leraar - iets dat in
Nederland ongehoord was. In Utrecht gaf Minnaert al voor de oorlog leiding aan
zoiets: natuurkunde-didactiekcolleges, vrijwillig te volgen. Ik heb onder
Minnaerts leiding, later samen met Mossel, zoiets mogen opbouwen - een schamele
lerarenopleiding, binnen de perken van wat een bestuursmaatregel (kb) en tegenstribbelende faculteiten toelieten. Ook maar een
kruimeltje tijd afstaan van de vakweten-schappelijke opleiding om het aan de
voorbereiding voor het leraarschap ten goede te laten komen - vergeet het maar.
Ik streefde een lerarendoctoraal na. Het is er gekomen, eerst aarzelend in de
vorm van pedagogiek en didactiek als klein bijvak, en ten slotte echt, zij het
met een vertraging van meer dan een kwart eeuw.
Ik was voorstander van een effectieve lerarenopleiding, liefst dat
lerarendoctoraal; daarvoor was ik door allerlei publikaties bekend. Dus werd ik
eens door het ‘Genootschap van leraren aan Nederlandse gymnasia en
lycea’ (tegenwoordig het ngl) uitgenodigd om (op
27 augustus 1952) tijdens hun landdag in Driebergen een lezing te houden,
‘De opleiding van de leraar in Nederland’, met als
tegenspeler Waszink, die echter verstek liet gaan. Ik heb mijn rede van toen
inmiddels meermalen herlezen. Er staat geen onvertogen woord in. Ik zou zeggen
dat wat ik daar uitte heden algemeen aanvaard is, in theorie en in de praktijk.
Maar toen? Bominslag, knuppel in het hoenderhok? Nee - dat werd het pas in de
verslagen van de grote pers. Ik denk veeleer dat ze me aanzagen voor een
wildeman, een clown, een op effectbejag verzotte demagoog. Toen ik samen met
Drewes (en een deelnemer die ons met de auto naar Utrecht bracht) vertrok, leek
het of we spitsroeden liepen. De secretaris schreef me later | |
| |
mijn
lezing toch maar liever niet te publiceren, omdat ‘niemand van de
leden erom gevraagd had’. Ik kreeg de tekst retour. Maanden later
vroeg de redacteur van het Christelijk Schoolblad Onze
Vacatures die er uit de pers van wist, het manuscript op om het te
publiceren. Het verscheen in drie afleveringen: op 7, 15 en 21 mei 1953.
‘Vakgeleerde of paedagoog’ was de titel - door de
redacteur vastgesteld. Misschien had het ‘of’ beter
‘en’ kunnen zijn. Maar het was inderdaad de strijd tegen
de negentiende-eeuwse fictie dat de gymnasiumleraar, de leraar een geleerde was.
Aan dit spinsel, dit weefsel mocht je niet tornen. Zodoende hebben de
Nederlandse universiteiten het overgrote deel van de lerarenopleiding uit hun
handen zien glippen en het was alleen maar op het nippertje dat ze er ten slotte
iets van konden redden. Misschien wordt dit nog eens met de herschikking van het
Hoger Onderwijs rechtgetrokken.
Ja, ik was een tamboer, maar voor dovemansoren. Daar schiet me net een gedicht
van Heine te binnen (sneu dat ik in het Duits - moet eindigen!)
Schlage die Trommel und fürchte dich nicht
und küsse die Marketenderin!
Das ist die ganze Wissenschaft,
das ist der Bücher tiefster Sinn.
Trommele die Leute aus dem Schlaf,
trommele Reveille und Jugendkraft,
marschiere trommelend immer voran!
Das ist die ganze Wissenschaft.
Das ist die Hegelsche Philosophie,
das ist der Bücher tiefster Sinn!
Ich hab' es begriffen, weil ich gescheit,
weil ich ein guter Tambour bin.
Nee, ik was geen goed tamboer. Een goede tamboer gaat niet diep in de nacht, maar
in de ochtend trommelen - als het tijd is om op te staan.
| |
| |
Maar denk niet dat ik er spijt van heb. Een enfant terrible hoort trots op zijn
ondeugden te zijn.
|
|