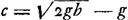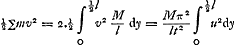Oeuvres complètes. Tome XVIII. L'horloge à pendule 1666-1695

[p. 489]

I.
Decouverte de la theorie generale de l'isochronisme des vibrations.
[1673 ou 1674]¹⁾

[Fig. 9.]

§ 1. Si arcus cycloidis AC [Fig. 9] dividatur utcunque in B, erit gravitas ponderis in A ad gravitatem ejusdem in B positi ut arcus AC ad arcum BC.

Est enim gravitas in A ad gravitatem in B ut gravitas super plano EC ad gravitatem super plano PC. hoc est ut PC ad OC, hoc est ut EC ad PC, hoc est ut arcus AC ad arcum BC²⁾. quod erat demonstrandum.

[Fig. 10.]

§ 2. CB est ∞ 2CA [Fig. 10]³⁾.

1) La Pièce, que nous jugeons être de 1673, est empruntée aux p. 411-415 du Manuscrit D. La p. 391 porte la date ‘ult. Jul. 1673’. La première date du Manuscrit E est le 19 décembre 1674. Nous divisons la Pièce en §§.

2) Huygens savait depuis longtemps (voir la p. 367, datant de 1659, du T. XIV) que l'arc CB [Fig. 9] est le double de la droite CP parallèle à la tangente en B; mais il ne paraît avoir remarqué qu'après la composition de l'‘Hor. osc.’ le théorème qu'il énonce ici, savoir que la composante du poids qui produit l'accélération est, dans le cas de la cycloïde, proportionnelle à l'arc correspondant se terminant au sommet. Or, comme il avait démontré l'isochronisme des vibrations dans le cas de la cycloïde, il put en conclure - voir le § 3 qui suit - que dans d'autres cas aussi où la force accélérante est proportionnelle à l'écart, la période doit être indépendante de l'amplitude.

3) Huygens considère ici une corde horizontale impondérable portant au milieu un point pesant A ou B décrivant autour du point C des circonférences de cercle: la tension est si grande qu'il n'est besoin de tenir compte que de la force centrifuge (et centripète). Si cette force etait absolument proportionelle à l'écart, il y aurait isochronisme des vibrations de différentes amplitudes d'après les Prop. I et III sur la force centrifuge (voir la p. 366 qui précède).

[p. 490]

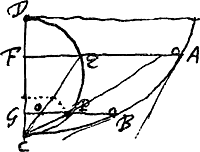
[Fig. 11.]

S'il demeure en B en tournant, il n'a que faire de faire le tour en si peu de temps que quand il demeure en A, c'est à dire qu'il ne luy faut pas double vitesse, puis qu'un moindre poids que double de celuy qui tient la corde en A est capable de la tenir en B. Donc les plus grands tours sont plus lents que les moindres. Mais en tant que les cordes EA, EB sont censees egales, les tours par B et par A sont isochrones.

§ 3. Ponatur pondus G aequale K [Fig. 11]. quaeritur ratio temporis per GF ad tempus casus perpendicularis per FH¹⁾.

AD²⁾ ∞ ½b. Unde arcus AE ∞ FG ∞ b [Fig. 12]. Atqui ut tempus per arcum cycloidis EA sit aequale tempori per GF [Fig. 11] oportet esse CA ⫟ AD - b ⫟ ½a ∞ ½GH nam GH censetur aequalis FH quia FG minima. Iamque incitatio ponderis in G³⁾ erit ad incitationem quam haberet in perpendiculari descendens ut FG ad ½ GH. ex legibus mechan.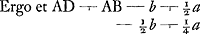

Sed AD est ½b. Ergo BA ∞ ¼a.

Est autem tempus per EA ad tempus per BA ut semicircumferentia BDA ad BA. Et tempus per BA ad tempus per FH ut 1 ad 2, quia dictum est BA esse ¼ a sive ¼ FH.

Ergo ex aequo, tempus per EA seu per GF ad tempus per FH ut semicircumferentia BDA ad duplam BA, sive ut quadrans circumferentiae ad diametrum BA.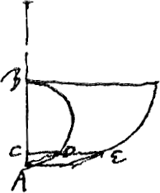

[Fig. 12.]

Ergo vibrationis integrae GL tempus ad tempus par FH ut semicircumferentia ad diametrum.

Ergo tempus vibrationis integrae GL aequale tempori semioscillationis⁴⁾ penduli longitudinem duplam FH habentis. hoc est tempori semioscillationis penduli SH.

Sit jam pondus K quadruplo gravius quam ante, ac proinde quadruplum ponderis G.

Jam quadruplo etiam, quam ante, majori pondere opus esset ad tenendam chordam inflexam angulo SGK.

Ergo pondus G jam quadruplo majori vi quam ante incitatur, tam in principio lineae GF, quam in singulis ejus punctis proportionaliter.

1) La corde tendue SGH est supposée impondérable; ou, si l'on veut, c'est une corde dont le poids, fort considérable, est supposé concentré en son point milieu. La corde étant verticale, la tension de la partie SG est supérieure à celle de la partie GH. Dans le § 1 Huygens ne tient pas compte de cette circonstance; il suppose la force agissant sur le poids G dirigée vers le centre du mouvement F. Mais dans le § 6 il revient sur ce sujet pour apporter la correction nécessaire. Le poids se meut ici, par hypothèse, suivant la droite GFL.

2) La corde (Fig. 12).

3) C.à.d. la composante, dans le sens du mouvement, de la force agissant sur le poids G. Comparez l'Avertissement qui précède.

4) Il s'agit de la moitié d'une oscillation simple.

[p. 491]

[Fig. 13.]

Ergo percurrit GF eodem tempore quo arcum ea [Fig. 13] cycloidis alterius aequalem ipsi FG, in cujus arcus principio e quadruplo magis incitetur quam in principio arcus EA prioris cycloidis.

Oportet igitur ac quadruplam esse AC [Fig. 12] et ad ∞ AD. sic enim arcus ea aequalis fiet arcui EA, et incitatio in e sive per rectam da erit quadrupla incitationis in E sive per rectam DA.

Jam vero cum ca, ad, ab sint proportionales apparet ba esse ¼ BA. Ideoque arcum ea percurri dimidio temporis quo percurritur arcus EA.

Ergo et GF, existente pondere K quadruplo ponderis G, duplo minori tempore peragetur quam ante cum pondus K ipsi G aequale esset.

Igitur qualicunque posita ratione ponderis K ad G, habebit tempus semioscillationis penduli SH ad vibrationem integram GL rationem subduplicatam ponderis K ad G⁵⁾.

Ergo etiam si vicissim velimus ut manente eodem pondere K vibrationes duplo celeriores fiant, oportet in G unam quartam prioris ponderis relinqui.

§ 4. Quaeritur proportio temporis ambitus circularis per circumferentiam cujus

5) Il résulte de ce calcul que dans le cas considéré - lorsqu'on ne tient pas encore compte de la correction nécessaire; voir les notes 1 de la p. 491 et 5 de la p. 493 - le temps de la vibration simple, de G à L, est π/2 √l/g √G/K, où g est l'accélération de la pesanteur et l = 2a la longueur de la corde. K est la tension de la corde, et G son poids concentré en son point milieu. En appelant - ce que Huygens ne fait point; comparez la note 5 de la p. 230 du T. XVI - m la masse du poids G, on peut écrire t = π/2 √ml/K.

[p. 492]

diameter minima GL, ad tempus casus per FH. vel potius ad tempus semioscillationis penduli SH.

Si incitatio ponderis in G esset aequalis gravitati ipsius G vel K, deberet tempus circuitus in circulo GL esse aequale duabus oscillationibus penduli longitudinis FG. per theorema ...¹⁾ nostrum de vi centrifuga. Nunc autem incitatio in G est ad pondus absolutum G ut FG ad ½ GH, hoc est ut b ad ½a. (nam GH censetur aequalis FH). Ut igitur fiat vis centrifuga aequalis incitationi seu pressioni chordae flexae super pondus G. debet fieri sicut b ad mediam proportionalem inter b et ½a, hoc est, sicut b ad √½ab ita tempus duarum oscillationum penduli FG ad tempus circuitus per circulum GL. Sit tempus oscillationis unius penduli FG, ∞ n. Ergo 2n√ ½ab/b ∞ tempus circuitus per circulum GL.

Verum ut b ad √2ab ita tempus oscillationis penduli FG ad tempus oscillationis penduli SH. Ergo hoc tempus erit n√2ab/b.

Erat autem tempus circuitus per circulum GL ∞ 2n√½ab/b seu n√2ab/b.

Ergo hoc tempus circuitus aequale tempori oscillationis penduli SH. ac proinde per ea quae pag. praeced.²⁾ duplum temporis vibrationis GL³⁾.

§ 5. Poteram pagina praeced.²⁾ brevius sic rationem colligere.

Est autem tempus per EA aequale tempori semioscillationis penduli duplam longitudinem BA habenti[s], hoc est longitudinem ½a, nam BA est ¼a. Ergo et tempus per GF aequale eidem semioscillationi penduli 2 BA sive ½a.

Sed haec semioscillatio est ad semioscillationem penduli SH ut 1 ad 2. Ergo tempus per GF aequale dimidio semioscillationis penduli SH. Ergo tempus totius vibrationis GL aequale semioscillationi penduli SH. vel oscillationi penduli dimidiae longitudinis FH.

1) Voir le théorème X à la p. 367 qui précède, ou bien la Proposition identique du Traité ‘De Vi Centrifuga’ à la p. 291 du T. XVI.

2) C.à.d. par le § 3.

3) Huygens ne calcule ici la période d'une vibration circulaire que pour le cas où la tension K et le poids G sont égaux. Il est évident qu'il eût pu tout aussi bien considérer le cas où cette égalité n'existe pas et qu'alors aussi il serait arrivé à la conclusion que le temps d'une vibration circulaire - c'est le cas déjà considéré dans le § 2 - est le double de celui de la vibration simple dans le cas du § 3. Cette période est donc, d'après ce théorème et la note 5 de la p. 491, T = 2t = π √ml/K.

2) C.à.d. par le § 3.

[p. 493]

§ 6⁴⁾. Si experimentum capiatur hujus rei, non succedet si filum SH perpendiculari situ tendatur, quia pondus G praeter incitationem à tensione quam facit K, incitatur etiam velut pendulum a perpendiculari SF extractum, hoc est velut si in plano inclinato, ad SG perpendiculari, jaceret.

Ad instituendum ergo experimentum deberet SH horizontali positu jacere, et pondus G alio praeterea filo perpendiculari longissimo superne distineri, ut ne infra rectam SH descendere posset. pondus autem K ipsi G aequale super trochleam appendendum.

Si tamen manente SH perpendiculari scire libeat tempus vibrationis GL, addenda est incitatio quae ponderi G ex ratione penduli SG advenit ad incitationem a flexu SGH ac pondere K effectam, et sicut summa haec ad mediam proportionalem inter hanc summam et incitationem a pondere K ita erit tempus vibrationis GL supra desinitum ad tempus verum vibrationis GL.

Incitationum rationes inter se sic colliguntur. Sit GP perpendicularis GS [Fig. 11]. Ergo incitatio ponderis G quatenus SG penduli vicem obtinet, est ad pondus absolutam G ut PF ad PG, seu ut FG ad GS sive FS, nam hae aequales censentur. Sed incitatio ex pondere K erat ad pondus absolutum G ut FG ad ½ FH vel ½ FS. Ergo incitatio ex ratione penduli dimidia est incitationis ex pondere K.

Ergo summa duarum incitationum ad incitationem ex pondere K ut 3 at 2. Estque inter 3 et 2 media proportionalis √6.

Ergo ut √6 ad 2, ita tempus vibrationis GL ante inventum ad tempus verum vibrationis GL.

Sed tempus vibrationis GL ante inventum aequale erat oscillationi penduli dimidiae longitudinis FH.

Cujus penduli oscillatio est ad oscillationem penduli quod ⅔ habeat suae longitudinis, seu ⅔ FH, sicut √6 ad 2. Ergo pendulum cujus longitudo ⅓ FH isochronas oscillationes habebit vibrationibus GL veris⁵⁾. Quod cum experimentis prorsus consentit.

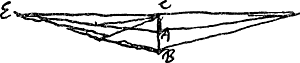
7⁶⁾. Sit celeritas puncti gravis A [Fig. 14], cum ex A in B venerit x. celeritas

4) Voir la fin de la note 1 de la p. 491. Nous ne possédons pas la relation des expériences dont il est question dans ce §. Comparez, sur des expériences de ce genre, le premier alinéa de la p. 265 du T. XVII.

5) Le temps d'une vibration simple dans le cas de la Fig. 11, les poids G et K étant égaux, n'est donc pas π/2 √l/g - comparez la note 5 de la p. 491 -, mais π/√6 √l/g.

6) Apparemment, Huygens considère ici une corde vibrante: ce n'est pas seulement le point ou élément A dont la ‘gravitas’ est θ, mais tous les autres éléments ont le même poids, ou, si l'on veut, la même masse; c'est ce qu'indique le mot ‘catena’. Comme dans le § 3 (p. 490), Huygens commence par considérer le cas où nθ (poids de la corde divisée en n éléments) est égal au poids p qui tend la corde.

[p. 494]

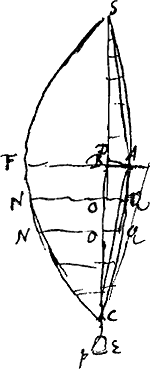autem quae acquireretur casu ex altitudine AB, sit c. Et linea AB sit b. AC ∞ a. pondus E ∞ p. gravitas puncti A sit θ. Et divisa intelligatur catena SAC in tot partes ut una sit ad omnes sicut pondus θ ad pondus p.

Jam ut qu. cc ad qu. xx ita erit AB ∞ b ad bxx/cc altitudinem ad quam ascenditur celeritate x. Sit ista bxx/cc aequalis BF¹⁾.

Jam si curva SFC sit ejus naturae ut applicatae FB, NO sint inter se ut quadrata applicatarum AB, QO²⁾, (ponitur autem SAQC parabola a qua insensibiliter differt²⁾) referent omnes NO altitudines ad quas ascenditur per celeritates acquisitas punctis singulis catenae SAC cum erit in recta SC.

Itaque singulae NO in singulas gravitates θ ductae, summa productorum omnium debebit aequari producto ex pondere p in descensum ponderis E, qui descensus aequatur 4/3 BD bis hoc est 8/3 BD. quia parabolam SAC eodem modo hic metimur ac si arcus circuli foret³⁾.

1) Puisque étant l'accélération de la pesanteur - on a BF = x²/2g. De même ON = x′²/2g, si nous appelons x′ la vitesse avec laquelle l'élément Q atteint le point O.

2) Huygens fait apparemment, outre l'hypothèse que la forme de la corde vibrante, dans sa position extrême, est à peu près une parabole, celle que tous les éléments de la corde exécutent des vibrations harmoniques: les vitesses x, x′ etc. avec lesquelles ils atteignent les points B, O, O, sont alors entre elles comme AB, QO, QO. D'après la note 1 BF : ON = x² : x′²; donc aussi BF : ON = AB² : QO².
Comme Huygens ne rend pas compte de ces hypothèses, nous ne tâcherons pas non plus de le faire. Il est possible qu'il ait songé à une forme sinusoïdale de la corde: voir la p. 528 qui suit, où il dit que la ‘linea sinuum’ dissère peu de la parabole.

2) Huygens fait apparemment, outre l'hypothèse que la forme de la corde vibrante, dans sa position extrême, est à peu près une parabole, celle que tous les éléments de la corde exécutent des vibrations harmoniques: les vitesses x, x′ etc. avec lesquelles ils atteignent les points B, O, O, sont alors entre elles comme AB, QO, QO. D'après la note 1 BF : ON = x² : x′²; donc aussi BF : ON = AB² : QO².
Comme Huygens ne rend pas compte de ces hypothèses, nous ne tâcherons pas non plus de le faire. Il est possible qu'il ait songé à une forme sinusoïdale de la corde: voir la p. 528 qui suit, où il dit que la ‘linea sinuum’ dissère peu de la parabole.

3) C'est, peut-on dire, une application de la loi de la conservation des forces (comparez le deuxième alinéa de la p. 471 qui précède), le produit du ‘poids’ p par le carré de sa vitesse étant supposé trop petit pour être pris en considération. Il est dommage que Huygens n'ait pas exécuté le calcul qui suppose évidemment les longueurs NO non seulement proportionnelles, mais égales aux plus grandes hauteurs que les différents éléments de la corde pourraient atteindre en s'élevant séparément avec les vitesses x, x′, etc.
S'il avait entrepris d'exécuter le calcul, il aurait peut-être été amené à considérer nettement la question des unités; il aurait pu dire qu'en formant le produit des ‘singulae NO [proportionnelles aux carrés des vitesses, d'après la note 2] in singulas gravitates θ ductae’, il faut prendre ½∑mv² - voir le deuxième alinéa de la note 6 de la p. 359 du T. XVI -, où m est le poids divisé par l'accélération g de la pesanteur.
En appelant t le temps d'une vibration simple, l la longueur et M la masse de la corde, et en répresentant par u le plus grand écart d'un élément de la corde de sa position d'équilibre - écart qui est égal à b pour le milieu de la corde -, on a v = πu/t et . Or, la valeur de cette intégrale est, pour une forme parabolique de la corde, 4/15 b²l. La ‘vis motus’ est donc 4π²/15 Mb²/t². En l'égalant à l'‘altitudo ducta in gravitatem’, c.à.d. au produit du poids p qui est Mg - puisque le poids tendeur est ici supposé égal à celui de la corde -, on a 4π²/15 Mb²/t² = Mgh, h étant la différence entre la longueur de la corde vibrante considérée dans sa position extrême et celle de la corde géométrique qui la soustend. Cette différence est d'après Huygens - comparez la p. 107 qui précède - ou 8/3 b²/l, puisqu'elle est supposée fort petite. Substituant h = 8/3 b²/l dans l'équation précédente, on en peut tirer t = π/√10 √l/g.
En supposant le poids tendeur (ou la tension) K - nous écrivons K au lieu de p pour nous conformer aux formules de la note 5 de la p. 491 et de la note 3 de la p. 492 - quelconque, nous aurions obtenu t = π/√10 √Ml/K, ce qui s'accorde fort bien avec la valeur actuellement considérée comme correcte t = √Ml/K. Comparez la fin de la note 10 de la p. 485.
Le calcul de la ‘vis motus’ du poids tendeur sait voir que celle-ci est en effet négligeable lorsque l'écart b est fort petit en comparaison de la longueur l.