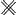Oeuvres complètes. Tome XX. Musique et mathématique
(1940)–Christiaan Huygens–
[pagina 111]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Notes se rapportant à des écrits de musicologues modernes.§ 1. aGa naar voetnoot1). Salinas: errat cum hexachordon minus item diapason et semiditonum multasque alias consonantias putat Harmonicè et Arithmeticè dividi a consonis intervallis. aeque ac diapason, diapente, hexachordon majus et aliae consonantiaeGa naar voetnoot2). Tonos 12 cum Zarlino et plerisque alijs statuitGa naar voetnoot3). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 112]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
§ 1. bGa naar voetnoot4). 1577 editus. Salinas lib. 3 cap. 27 de prava constitutione cujusdam instrumenti scribit in Italia ab annis 40 instrumentum fuisse fabricatum, incerto auctore, in quo tonus omnis in 5 partes aequales divisus erat, diapason in 31, semitonium majus 3, minus 2 partes habebat. Idque a magni nominis musicis in pretio habitum. Deinde docet quomodo tonum illi in 5 partes aequales diviserint, nempe sumendo ab utroque termino semitonium majus, et ab horum terminis rursus semitonium minus. quam divisionem merito carpit quia non hoc modo in 5 aequalia tonus secaturGa naar voetnoot5). Sed quod sensui ingratam esse hanc positionem asserit, fallitur. Recte enim se habet ad sensum, et a vera nihil pene differt ut demonstrabo. Dicit non credere se quartum temperamenti genus inveniri posse. dicit illos semiditono tribuere dieses ejusmodi 8, ditono 10, diatessaron 13, diapente 18, diapason 31. quod recte. Saepe se expertum ait hoc modo disponere instrumentum sed ingratum auribus omnium sonum prodijsse, eoque hoc temperamentum ab omni harmonica ratione tam perfecti quam participati instrumentiGa naar voetnoot6) abhorrere conclusit. Toto capite de hoc agit. Proculdubio non bene experimentum instituit. § 1. cGa naar voetnoot7). Franciscus Salinas De Musica lib. 3 cap. 15Ga naar voetnoot8), tria genera Temperamenti | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 113]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
inventa ait, quorum primum sitGa naar voetnoot9), ut Comma, cujus ratio est 81 ad 80, dividatur in partes aequales tres; quarum una augeatur Tonus minor, (cujus ratio 10 ad 9) et duabus diminuatur Tonus major (cujus ratio 9 ad 8). Secundum Temperamentum statuitGa naar voetnoot10) in quo Comma in 7 partes aequales distribuitur, quarum partibus 4 diminuatur tonus major; minor verò augeatur tribus. Denique et Temperamentum Tertium idque optimum, exponit cap. 22Ga naar voetnoot11). Caput 27 eodem lib. 3oGa naar voetnoot12), hanc habet inscriptionem: De prava constitutione cujusdam instrumenti quod in Italia citra quadraginta annos fabricari coeptum est, in quo reperitur omnis Tonus in partes quinque divisus. Ait ignoti authoris esse, et archicymbalum vocatum. In eo semitonium majus habere ⅗ toni. Semitonium minus ⅖. A quibusdam magni nominis musicis in pretio habitum dicit et usu receptum, eo quod omnis in eo sonus habeat omnia intervalla et omnes consonantias (ut illis inquit videtur) inferne et superne, et post certam periodum ad eundem aut aequivalentem sibi sonum post 31 intervalla reditur &c. Diapason in partes 31 aequales ipsis divisa est, quarum partes 5 habet tonus, semiditonum seu tertia minor 8: ditonum seu tertia major 10; diatessaron 13; diapente 18. Ex ijs quae de modo dividendi toni in partes 5 exponit quo illi utebantur, apparet ipsos ignorasse qua ratione id perfici posset. Hinc contra illos argumentatur, non dividere eos tonum in quinque dieses ut putabant. Deinde facto experimento tantum se ait invenisse consonantiarum imperfectionem ut eam aures pati non possent. Hanc tamen divisionem, atque hoc temperamentum optimumGa naar voetnoot13) esse nec sensibiliter ab illo tertio quod in usu est, differre, ostendimus inventa per Logarithmos vera divisione octavae in 31 partes aequales; fiunt enim diapente 1/110 commatis majores quam in vulgari illo Temperamento, adeo ut paulo meliores efficiantur. Cap. 28Ga naar voetnoot14) vult in violisGa naar voetnoot15) semitonia omnia esse aequalia, ut olim puto Aristoxe- | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 114]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
nusGa naar voetnoot16). Sed nihil vetat quin efficiantur inaequalia ut in cymbalis nostris et organis, quoniam non opus est chordas omnes ijsdem divisionibus secari, a transversarijs illis collo illigatis, quae ijs locis ubi opus est, uni chordae attribui possunt, ac separatim defigi, ut vera semitonia efficiant. Cap. 31Ga naar voetnoot17). Paralogismus est, quod lineam extrema et media ratione continuè divisam putat exhibere divisiones semitoniorum in violis.
§ 2Ga naar voetnoot18). Zarlino lib. 3 cap. 6Ga naar voetnoot19). Etsi Didymus ac Ptolemaeus tertiam majorem perfectam inter secundam quartamque chordam collocaverint, neuter tamen eam consonantijs adnumeravitGa naar voetnoot20). Mersennus et alij contrarium dixeruntGa naar voetnoot21). unde putabam illos alia Ptolemaei scripta legisse, quorum ego copiam non habuissem. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 115]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Zarlin. Ragionamento 4. proposta 1. dicit Temperamentum ab alio - quem qui fuerit nescit - et casu fuisse inventumGa naar voetnoot22). Item lib. 4. cap. 12. Supplementorum Musicalium multum laudat hoc inventumGa naar voetnoot23). Institut, lib. 2. cap. 42Ga naar voetnoot24). Temperamentum non optimum docet in quo 3tiae majores et minores aeque multum a perfectione absunt, et quintae quartaeque 2/7 commatis. Et cap. 43. demonstrare contendit aliud temperamentum tolerabile non dari, et improbat illud quod tono majori adimit ½ comma ac tantundem tono minori addit. quod tamen verum atque optimum est temperamentumGa naar voetnoot25). sed ab illo tunc non adhuc bene perspectum. ita enim proponit ut 5tas et 4tas relinquat perfectasGa naar voetnoot26). SalinasGa naar voetnoot27) idem explicat et pretend l'avoir trouvè aussi bien que Zarlin, c'est a dire l'explication ou demonstration. il parle seulement des Instit.ons de Zarlin et non pas des demonstrations ou le vray temperament doceturGa naar voetnoot28), et que Zarlin dit avoir estè imprimees auparavant le livre de SalinasGa naar voetnoot29). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 116]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Mon opinion est que le Temperament veritableGa naar voetnoot30) a estè longtemps auparavant pratiquè par les organistes &c. seulement a l'ouie en diminuant un peu les quintes, sans examiner aucunement la proportion de cette diminution qui n'appartenoit qu' aux geometres. Et la pluspart des organistes l'ignorent encore et j'en ay trouvè qui nioient que les tierces majeures et 6tes mineures fussent justes.
Zarlini Instit.s et Demonstr. eodem anno 1589 editas habeo. Supplementis adscribitur annus 1588Ga naar voetnoot31). Nescio an non Institutiones ante editae fuerintGa naar voetnoot32). At in institutionum editione hac allegat demonstrationum opus, de participatione seu temperamento loquens parte 2da cap. 41. ubi trium temperamentorum meminitGa naar voetnoot33), sed unum tantum explicat et admittit ubi 2/7 commatis diminuuntur 5taeGa naar voetnoot34). At in demonstrationibus prefert omnibus illud ubi ¼ commatis aufertur 5tisGa naar voetnoot35). Hinc plane opinor Institutionum secundae editioni aliquid fuisse adjectumGa naar voetnoot36). Cap. 47. Parte 2 Instit.Ga naar voetnoot37) Clavicymbalum suae inventionis describit ubi adjunctae sunt chordae Enarmonicae praeter Chromaticas. Tonum ibi ait divisum in 4 partes. Ego in 5 partes eum divido. Palmulas bene ordinat, sed tamen difficultas erit in sonando quod enarmonicarum et chromaticarum vicinia faciet ut saepe duae simul pro una deprimantur.
Il fait fort valoir ce qu'il scait de la geometrie, ce qui ne regarde que les proportions comme tousles autres qui ont fait les docteurs en musique Boethius, Glareanus, Salinas. Il a brouillè tout par le meslange de la musique anciene et de ses termes parmi la moderneGa naar voetnoot38). comme en nommant les tons par les noms des Grecs hypate hypaton trite diezeugmenon &c. et parlant tousjours des tetrachordes. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 117]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Il se glorifie beaucoup d'avoir trouvè qu'on chante aujourdhuy l'espece de diatonique que Ptolomee nomme syntononGa naar voetnoot39). ce qui est vray; s'entend meslee des chordes chromatiques. Dans ses demonstrations harmoniques ou il enseigne le bon et veritable temperamentGa naar voetnoot40) il n'adjoute pas les demitons ou tons chromatiques, ni mesme le C♭. Et ainsi il n'a pu remarquer deux quintes et 2 quartes que l'on gagne par ce temperament. qui sont C♭F et CF♯ quintes et FC♭, F♯C quartes. Ces consonances estoient imparfaites dans le monochorde diatonique ou les quintes et tierces sont parfaites. Et le remede du double D ou RE ne faisoit rien a cellescy, quoyque il donnast la quinte parfaite RL, et par consequent la quarte parfaite LR, comme il a remarquèGa naar voetnoot41); mais il ne devoit pas dire que c'estoit gagner 2 quintes et 2 quartes car ce n'est qu'en considerant le systeme de 2 octaves de suite depuis L a L3 ou il a deux fois RL et LR.
En adjoutant les tons chromatiques aux diatoniques on n'avoit pas le S♯, ni le M♭. Sur les instrumens qui n'avoient que les sons diatoniques ils ne pouvoient pas faire les cadences RV♯R,SF♯S, LS♯L.
Cap. LXXIX tertiae partis instit.Ga naar voetnoot42) existimat antiquos musicos cantum ita junxisse lirae citharae alijsque organis ut fuerit quod nunc appellatur un faux bourdon d'octave quinte et quarte. Vel etiam absque cantu, putat altera manu easdem chordas istius faux bourdon sonare solitos, dum alterâ cantilenam isti consonantiae accommodatam exprimebant simplicibus tonis. Et haec sententia vero non est absimilisGa naar voetnoot43). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 118]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Cap. 75 parte tertia Instit. Zarl.Ga naar voetnoot44) incompositum intervallum vocatur ex. gr. semiditonus in Genere chromatico, ditonus in Enarmonio quod illic absque ullo sono medio accipiantur. Est enim MFF♯L tetrachordum chromaticum. MM♯FL tetrachordum enarmonium. Idem ditonus et semiditonus in genere diatonico vocantur intervalla composita. Non bene mihi videntur uti signo ˟ ad notandos sonos enarmonios. melius enim signis ♯ et ♭ omnia perficiuntur, quorum illud indicat appositionem semitonij minoris sursum seu in partem acutiorem; alterum vero remissionem similis semitonij deorsum seu in partem graviorem. Cap. 74 ibid.Ga naar voetnoot45). Si ad veterum normam cantum componere libeat, nihil vetat generibus quibusque simpliciter uti; si vero concentum desideremus qualis hodie viget, frustra conabimur uti chromatico vel enarmonio solis. Cap. 19. Rag. 1Ga naar voetnoot46). Male supponit terminos datos quibus medius prop. harmonicè inveniendus est differre inter se unitate. deinde in demonstratione plane παραλογίζει. Duodecima, octava, sexta major, quinta a tono intermedio consono harmonice dividuntur non autem 6a minor licet ipsa quoque tonum intermedium consonum bifariam recipiat.
§ 3 aGa naar voetnoot47). MaillardGa naar voetnoot48) escrit que l'octave contient moins de 6 tons. Salinas croidGa naar voetnoot49) que la sixte mineure se divise authentiquement et harmoniquement par la tierce mineure en bas et par la majeure, ce qui est faux. Et il assure la mesme chose de plusieurs autres consonances ou cela n'est pas vray non plus. § 3 bGa naar voetnoot50). P. Maillard des modes imprimè 1610Ga naar voetnoot51). Chap. 10Ga naar voetnoot52). Il parle de l'addition | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 119]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
du Sy aux 6 notes de Guido, et mesme de o pour huictieme qui fait l'octave du VtGa naar voetnoot53). Et dit que l'an 1574 qu'il demeuroit a Anvers on ne parloit entre les musiciens que de ces nouvelles notes. Il mepriseGa naar voetnoot54) cette invention, disant qu'apres le LA on fait suivre tantost un ton entier et tantost un demi-ton, et que partant on ne scauroit donner un certain nom a la note apres le LA: voila une bonne raison! Il loueGa naar voetnoot55) extremement l'invention des 6 notes de Guido et croit qu'il ait voulu indiquer par la les 6 modes authentiquesGa naar voetnoot56). Et comme le Sy ou Ci ne peut constituer un mode pour n'avoir de 5 en haut ni 4 en bas, c'est pour celaGa naar voetnoot57) qu'il croit ce ton indigne d'avoir un nom. Il ditGa naar voetnoot58) que Eric Puteanus dans son traitè Musathenum adjoute aux 6 notes de Guido le BIGa naar voetnoot59). Il avoueGa naar voetnoot60) que par cette methode on apprend facilement a chanter | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 120]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
toute sorte de musique, mais pour parvenir a la connoissance des modes il soustient qu'il faut suivre celle de Guido. Et il a tortGa naar voetnoot61).
§ 4. aGa naar voetnoot62). Mersenne liv. 5 prop. 34Ga naar voetnoot63). nomme le MaireGa naar voetnoot64) qui avoit divisè le ton en 4 parties sur son luth. Et TitelouzeGa naar voetnoot65) qui l'avoit divisè en 3 parties egales sur une spinette particuliere. l'un et l'autre ne valoit rienGa naar voetnoot66). Il dit que S. Augustin parle de la mesure qu'on bat qu'il nomme PlaususGa naar voetnoot67). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 121]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
§ 4. bGa naar voetnoot68). De la division du monochorde et de l'accord des instruments. Aristoxene divisoit l'octave en 12 demitons egaux, ce que Vincent GalileeGa naar voetnoot69) maintient estre la meilleure division. Mersenne s'en sert pour le luthGa naar voetnoot70). Du vray temperament et accord des instruments. Mersenne raporte pag. 73 et 74 des Instruments les divers genres de Diatonic, Chromatic et Enharmonic de plusieurs anciens, tous peu propres a la musiqueGa naar voetnoot71) et qui montrent qu'ils ne chantoient pas a plusieurs partiesGa naar voetnoot72). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 122]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
rf♯ l u♯ rf l u les 2 accords nouveaux du luth l'un par b quart l'autre par b mol. C'est depuis la 4e chorde jusqu'a la chanterelle. u l f r l m r u c l tout l'accord nouveau par b mol du descendant de la chanterelle.
Raison des differents sons que rend une mesme chordeGa naar voetnoot73); et des sons de la trompette marine, et de la trompette. Du son des anches, qu'on baisse leur ton en mettant des morceaux de cire sur les languettesGa naar voetnoot74). Que les tuyaux ouverts et a anches ne font pas plusieurs tons mais seulement les bouchezGa naar voetnoot74). S'il est vray que des tuyaux de mesme longueur mais plus gros les uns que les autres font de tons differents de 5 ou 6 intervalles comme l'assure Mersenne. Le moindre avoit 3 lignes de diametre. tous 6 pouces de long. les autres 6, 12, 24, 48 lignes de diametreGa naar voetnoot75).
Pag. 342 des Orgues. Apres avoir bien expliquè le temperament, il dit qu'on n'en peut user qu'en mettant 20 marches a l'octave, et que Salinas le prouve au livre 3. chap. 33. Que pour cela il faut faire les 12 demitons egaux comme au luthGa naar voetnoot76). Mal!
Voyez encore sur Mersenne la note 21 de la p. 114 et le § 5b qui suit. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 123]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
§ 5. aGa naar voetnoot77). Kircher MusurgiaGa naar voetnoot78) l. 1. cap. 6. digressione. an in vacuo fieri possit sonusGa naar voetnoot79). Experimentum indiligenter factum refert, eoque aerem in phiala experimenti toricelliani restare probat quod sonus campanulae inclusae audireturGa naar voetnoot80). aquam ad 10 pedes constitisse ait. unde non bene rem peractam liquetGa naar voetnoot81). in vacuo tamen si daretur putat sonum non fieri. Experimentum Florentinum similiter sonum fuisse auditum asseritGa naar voetnoot82). Meum vero contraGa naar voetnoot83). L. 5. c. 2Ga naar voetnoot84). inventum Guidonis Aret.Ga naar voetnoot85) valde laudat quod mihi non videtur | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 124]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
laude dignum. Cum jam ante lineis uterentur 8 et Elementis literarum septem sonos octavae significarentGa naar voetnoot86). Guidonem refert ad annum 1024. 300 annis post ait Ioannem de Muris Parisinum ultimam manum imposuisse guidonianae musicae, inventis notis quae tempora prolationis simul notarentGa naar voetnoot87). Dicit ibidemGa naar voetnoot88) Guidonem invenisse primum symphoniam plurium vocum. Id constare ex praefatione Micrologi ad Theobaldum Episc. AretinumGa naar voetnoot89). Edidit hunc Microl. sub papa Ioanne 2Ga naar voetnoot90). Vellem videre. dicit et auctorem fuisse instrumentorum polyplectrorum ut clavicymb. &c. Sed fallitur puto nam organa et hydraulica etiam polyplectra erant jam diu ante ejus tempora, nisi tantum quae fidibus tenduntur hoc nomine censenda sintGa naar voetnoot91). L. 6 c. 1. theor. 9. de cognoscendo numero diadromorum chordaeGa naar voetnoot92). Mersenni habet experimentumGa naar voetnoot93). chorda 17 pedum ex 12 intestinis tensa pondere ½ librae, bis currit et recurrit in minuto secundo. duabus libris tensa quater recurrit. 8 libris octies. Contradicit huic experimento ob difficultatem quod ubi primum vibrationes numerabiles fiunt sonus amplius audiri nequeat. stolidè. sufficit enim cognita proportio numeri vibrationum subdupla rationis ponderum quibus tenditur. Guido promittitGa naar voetnoot94) menstruo spatio discendum quod antea vix multis annis etiam | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 125]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ingenio pollens didicisset. quanta ergo difficultas illa prisca fuerit cum et Guidonis methodus tantum tricarum habeat. L. 7 c. 5.Ga naar voetnoot95). Improbat consuetudinem componistarum ad clavicymb. sua examinantium. vultque absque illo per scientiae regulas symphoniam condi. ineptè. Recte ibidemGa naar voetnoot96) reprehendit illos qui vocibus singulis cantum accommodant non vero argumento, contra quod sepe peccant. ut qui ad verba illa seu themaGa naar voetnoot97), Absterget Deus omnem lachrymam ab oculis eorum ubi nullus luctus clamor aut dolor, plurimum ludit in verbis illis lachrymam luctus dolor, hoc agens omnibus modis ut tristem cantum, tristes clausulas, ijs accommodaret. Quid autem lachrymae, dolor, luctus cum celestibus gaudijs commune habent. alterum exemplum refert mors luctuosa festinatGa naar voetnoot98); ubi illud festinat incitatis notis et mirè discurrentibus exprimit contra decorum.
Lib. 7. Exempla affert moesti cantusGa naar voetnoot99). Mihi videtur non adeo lentis syllabis dolorem exprimendum, ut nonnunquam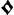 Ga naar voetnoot100) singulis dentur; sed prorsus imitandum tenorem sermonis qui non multo lentior est plangentibus quam loquentibus. Ga naar voetnoot100) singulis dentur; sed prorsus imitandum tenorem sermonis qui non multo lentior est plangentibus quam loquentibus.
Vellem etiam ut non quae artificiosissima sunt et inventu difficilia sectarentur melopoei nostri sed quae aures maximè afficerent. Quid enim mihi cum imitationibus accurate servatis, quas fugas vocant, quid cum duplicibus, si absque his ut liberior ita et gratior efficitur melopoeia. Artifices istis se delectari dicunt, non tam dulcedine concentus affectos quam consideratione artificiosae compositionis; qui non recte hoc pacto melopoeam aestimant, cujus finis est delectare sono quem auribus percipimus, non contemplatione artis. Haec enim diversa sunt. Illi vero artem magis ex regulis quibusdam quas sibi finxere et quibus saepe nimis tenaciter inhaerent, quam ad effectum harmoniae judicant. Ars autem nisi naturam moveat ac delectet nihil sane egisse videatur, ut Cicero inquitGa naar voetnoot101). Itaque illam sibi | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 126]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
unicè artem proponant quâ auditores delicatas aures habentes delectareGa naar voetnoot102) possint, sed ita ut et imperitioribus voluptatem pariant. Unde enim origo praeceptorum nisi ab ijs rebus quas probabant suavesque sentiebant nondum ullis praeceptis imbuti. Quamobrem nec praeceptis ita considere debent ac si geometriae axiomata essent, sed multas exceptiones dari existiment semperque fixum illud teneant, propositum delectationem adferre auribus prius quam artis examen instituatur.
§ 5 b. Apud MersennumGa naar voetnoot103) disputatur an gratior sit concentus monodijs nec rationes desunt.
§ 5 c. In methodo Guidonis illud operam dedit ut semitonium majus syllabis mi fa tyrones semper exprimerent, cum tamen tonum quatuor modis canant nempe UT RE, RE MI, FA SOL, SOL LAGa naar voetnoot104).
§ 5 d. Kirch. tom. 1. l. 7. Erotemate 4Ga naar voetnoot105). Explicat notas musicas odes Pindaricae χρύσεα ϕόρμιγξ ἈπόλλωνοςGa naar voetnoot106). Strophe notas τῆς λέξεως habet sive quae cantum dirigunt. antistrophe notas τῆς ϰρούσεως instrumento sequendas, sed tamen et his verba subjiciuntur. Modus est Lydius quod ex figura notarum patetGa naar voetnoot107). Cantus autem videri potest esse Toni MLMGa naar voetnoot108) nisi quod finit in R. Kircherus finit eum in G, sed | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 127]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
hoc nihil refert cum idem ipsi ac mihi fiat cantusGa naar voetnoot109). In fine notas quasdam male explicaverat quas correxiGa naar voetnoot110). pag. 593 et 594Ga naar voetnoot111). Exemplum CapspergerianaeGa naar voetnoot112) melopoeae recitat  § 5 d. Si per omnes tonos ita discurrere licet ut diu in illis maneant, aut saltem ad primum non redeant, quidni et in alio tono finire permittant; et sane vidi in Italorum melismatis ubi hoc factitarunt, incipientes in SVS, sunt qui finiunt in MCM. Hoc vero ut ineptum est ita etiam vagatio ista per tonos alienos ut plane ejus in quo coeperant obliviscantur. Hoc enervat vim ac decorem cantus nec perinde delectat auditores ac constans modulatio quae tonum servat vel ita certe excurrit ut continuo revertatur. Necesse est vocem canentis ope instrumenti dirigi et in ordinem cogi ne a tono | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 128]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
evagetur. nam si verbi gr. canat 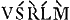 , hoc ultimum M non erit tertia major ad V sed toto commate altius veroGa naar voetnoot113). , hoc ultimum M non erit tertia major ad V sed toto commate altius veroGa naar voetnoot113).
§ 6Ga naar voetnoot114). Ad Jo. van der ElstGa naar voetnoot115). Ouden en nieuwen grondt vande musycke. Gedruct te Gent. 1662Ga naar voetnoot116). Sex syllabas Guidonis Aretini retinetGa naar voetnoot117) ideoque mutationes quas vocant, discentibus difficillimas, cum addito si, cuique tono suum nomen tribuatur. SemitonijsGa naar voetnoot118) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 129]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
sua nomina dat fi, sil, it, ri, item at, ra, ma, sal, quod fieri potest, sed non est tam necessarium atque vox si. Duae perfectae consonantiae non debent sese consequi. ut quintae, octavae, unisoni. Rationem absurdam redditGa naar voetnoot119) quod audita perfecta consonantia, plane acquiescat sensus; ideoque ne nausea sequatur subjungendam imperfectam. Nam primo divisio illa in perfectas et imperfectas consonantias inepta est. Deinde non sequitur dulcedo aut satietas nimia cum duae quintae sese sequuntur, sed contra offenduntur aures rudi ac dura illa consonantiarum successione quia subito quasi in alium Tonum transitur; nam etiam tertiae intermediae vel accedunt, vel subaudiuntur. Octavae vero continuatae improbantur, quod eadem modulatio Bassi et Cantus nequaquam satis faciat expectationi auditoris, cui gratiores essent aliae consonantiae quintarum et tertiarum. Si pluribus Choris canatur. debent Bassus diversorum vel unisonis vel octavis vel interdum tertijs inter se referri, nunquam vero quintis.
Dans son ‘Bericht’ de 1732, mentionné à la p. 69 qui précède, Q. van Blankenburg, qui connaît aussi les ouvrages de van der Elst, écrit: ‘Wat aangaat de namen Si en Sa, It en Ut, die heb ik in den jare 1681 met den Ed. Heere Christiaan Huygens vastgestelt, en zijne zwarigheid, dat men de naam Ci (die men in d'oude musiec vind) in geen Ca mogt veranderen door 't verwisselen van die C in een S, weggenomen; in dezelfde tijd heeft zijn Ed. zijn Cycle Harmonique van 31. klanken in 't octaaf in cyffer gestelt, en bij de Mi een Ma gevoegt’, etc. Comparez le § 3 à la p. 167 qui suit.
À la même p. du Man. G Huygens cite aussi Ludovicus Viadana: voyez les Additions et Corrections. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 130]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
§ 7Ga naar voetnoot120). SimpsonGa naar voetnoot121). Compendium Musicae Angl.eGa naar voetnoot122). Varios effectus modorum apud veteres, ortos inde existimat, quod praeter diversa intervalla cantus etiam diversitatem mensurae seu rythmi contineantGa naar voetnoot123). Quintas perfectas et imperfectas eleganter poni deinceps censet, in notis non longisGa naar voetnoot124).
En b mol l'on fait des cadences sur la note medianteGa naar voetnoot125). Mais cela n'est pas aisè en ♮; mais alors il veut la cadence mediante à la seconde ou quarte plus haut que la finale. Ainsi dans le ton de VSV les cadences mediantes seront en R ou F. J'y adjoute encore la cadence imparfaite ou le dessus finit en M et la Basse en L.
Christoph. Simpson escrit que de C♭ a Ci est le demiton majeur et de Ci a V le demiton mineur, justement a rebours, et de mesme dans tous les autres demitonsGa naar voetnoot126). Il croit aussi que le triton et la fausse quinte sont des intervalles egauxGa naar voetnoot127). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 131]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
§ 8Ga naar voetnoot128). Sur un traicté de Musique de M. Perrault le medecinGa naar voetnoot129).
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 132]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 133]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Qu'il est assez disputable si les musiciens modernes avec leur contrepoint figurè ou l'on prononce des paroles differentes en mesme temps, sont dans le bon chemin.
§ 9Ga naar voetnoot143). Andr. WerckmeisterGa naar voetnoot144) Organist zu Quedlinburg (en marge: author ineruditus ac parvi pretij) improbat Temperamentum optimum quo quintae diminuuntur ¼ commatisGa naar voetnoot145). Errat autem in eo quod ab omnibus chordis tam diatonicis quam chromaticis putat diapente sursum postulari in hoc TemperamentoGa naar voetnoot146). Incipit enim ab V, S, et procedit ad S, R; R,L; L,M; M,Z; Z,F♯; F♯ U♯; U♯ S♯ ac porro ponit etiam S♯ d♯ seu S♯ e♭; malè, hoc enim nemo ut puto sic statuit; hinc rectè pergit per E♭B (seu ut ille D♯B); B, f; F, c. Iam dicit 2 commatis inveniri gravius hoc c quam ut ad C imum diapason efficiat. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 134]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
VideturGa naar voetnoot147) cum alijs authoribus (e quibus GibeliumGa naar voetnoot148), BaryphonumGa naar voetnoot149) allegat) optimum temperamentum statuere hujusmodiGa naar voetnoot150).
ubi D auxiliare apponiturGa naar voetnoot152). Intervallum vero Gis, Dis, ponitur diapenteGa naar voetnoot153). Hanc vocat unserer TemperaturGa naar voetnoot154) et in monochordi figura primum collocat et huic tantum ac 6to Temperamento numeros adscribit. sed hic nihil temperatum. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 135]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 136]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
§ 10Ga naar voetnoot159). Thomas SalmonGa naar voetnoot160) (mag. art. in Colleg. Trin. Oxon. impr. 1672) An Essay to the avancement of musickGa naar voetnoot161). Docet absque clavibus vel potius unica musicam omnem commodè scribi, in quinque lineis quarum infima semper sit locus soni G seu solGa naar voetnoot162). Idemque vult fieri in singulis partibus quas vocant ut Basso Tenore SuperioGa naar voetnoot163).  Singulis octavam suam tribuendo per diapason a proxima differentem quas litera prefixa discriminat. B Bassi diapason notat. T tenoris (apud ilium T est Trebble seu superius), C Cantus. Tum si longe ultra lineas excurrant notae ad altiorem inferioremve diapason referuntur praeposita litera ejus partis indice, sic  quae mutatio percommoda est quod distantia per diapason mutetur. Haec meo judicio non contemnenda est inventio, atque eo facilius in usum recipienda, quod, Clavis Bassi ordinaria, ijsdem locis sonos signet atque haec methodus: nec non et supremae partis clavis una, ut nihil novi addiscere sit necesse. utilitas autem et discentibus musicam et componentibus concentus non exigua hinc oritur. |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||