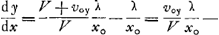Oeuvres complètes. Tome XXI. Cosmologie
(1944)–Christiaan Huygens–
[pagina 489]
| |
Appendice I
| |
[pagina 490]
| |
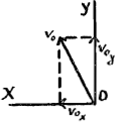
L'asymptote verticale se trouve à une distance xo = vox/k de l'origine O. On peut modifier ces expressions en y introduisant la ‘vitesse finale’ (d'une chute verticale) V = g/k. L'équation (1) fait voir que l'ordonnée y est la différence y1 - y2 des ordonnées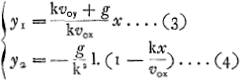 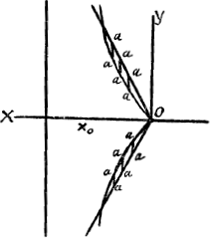 [Fig. 138]
De ces équations la première représente [Fig. 138, partie supérieure] une droite passant par O, la deuxième une logarithmique possédant la même asymptote que la courbe du jet. Pour obtenir la courbe du jet il faut donc faire descendre sur l'axe des x toutes les petites droites verticales aa: la courbe cherchée passera alors par leurs sommets. Dans les figures de Huygens il en est à peu près de même; seulement la droite et la logarithmique y ont une autre position; c'est celle qu'on obtient, comme nous l'indiquons dans la figure, en prenant l'image ou inverse de la droite et de la logarithmique par rapport à OX, ce qui évidemment ne modifie pas les longueurs des droites aa qu'on peut faire descendre, comme le fait Huygens, sur une horizontale plus basse. 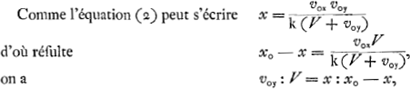 ce qui correspond à une équation de Huygens suivant laquelle le rapport voy : V est égal à AK : KD [Fig. 134]; ou bien, dans les Fig. 63 et 64 de la p. 117 du T XIX, ϑχ : ζ = CA : BA. Mais la droite et la logarithmique des figures de Huygens ne sont cependant pas identiques avec celles considérées ici; puisqu'il construit d'abord une autre courbe [Fig. 64] qui ne se change en courbe du jet que lorsque toutes les ordonnées sont multipliées par un facteur constant.
Désignant le ‘latus rectum’ de la logarithmique de Huygens par λ, comme il le | |
[pagina 491]
| |
fait à la p. 117 du T. XIX, et prenant les axes comme dans la présente figure 139, l'équation de cette courbe est 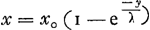 ou ou 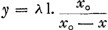 .... (5) .... (5)
 [Fig. 139]
AN [Fig. 64] étant la tangente à cette courbe en A, on a, en annulant y dans dy/dx = λ/x0 ey/λ, 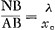 . Or, AB = xo; donc NB = λ. . Or, AB = xo; donc NB = λ.
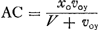 ; les coördonnées du point D sont donc ; les coördonnées du point D sont donc
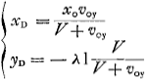 et la direction de la tangente E D O en D à la logarithmique est déterminée par l'équation 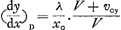
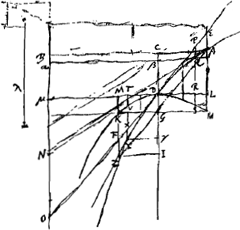 Fig. 64
de la p. 117 du T. XIX 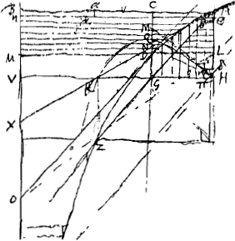 Fig. 65
de la p. 119 du T. XIX | |
[pagina 492]
| |
Comme la direction de la droite (3) était déterminée par 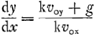 ou ou 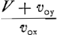
on voit que le facteur conctant dont il était question plus haut devra se montrer égal à xo/λ · V/vox. L'équation de la droite A G Z [Fig. 64 et 65] parallèle à E D O sera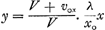 ... (6). ... (6).
D'après les équations (5) et (6) la courbe considérée par Huygens (l'‘analogistica luxata’) qui devra se changer en courbe du jet sera 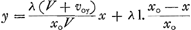 ... (7) ... (7)
tandis que l'équation (1) était 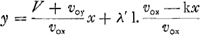 ...(1′) ...(1′)
en appelant λ′ le ‘latus rectum’ g/k2 de la logarithmique qui y figure. Les expressions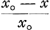 et et 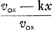 sont identiques puisque vox = kxo. sont identiques puisque vox = kxo.
Multipliant ensuite l'un et l'autre terme du second membre de l'équation (7) par xo/λ · V/vox ou g/k2λ on obtient, comme il le fallait, le second membre de l'équation (1′). Reste à faire voir que ce facteur est bien celui dont parle Huygens. Dans la Fig. 65 il l'indique par GM/GN. Comme dans cette figure HM est la direction de la vitesse initiale, autrement dit que c'est la tangente à la courbe du jet, on a GM/GH = voy/vox. D'autre part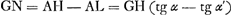 en désignant par α et α′ les angles que font respectivement avec l'axe des x les droites AZ et AN. C.à.d. en désignant par α et α′ les angles que font respectivement avec l'axe des x les droites AZ et AN. C.à.d.
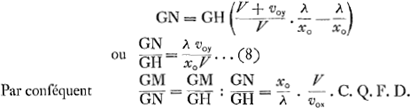 | |
[pagina 493]
| |
Dans la Fig. 134 de la p. 481 le facteur est désigné par TL/BP, ce qui, vu l'équation SP : PB = RL : LT, correspond à RL/SP. Or, en comparant les figures, on voit que RL est la même chose que MG de la Fig. 65 et SP la même chose que NG. Nous avons donc constaté l'identité qu'il s'agissait d'établirGa naar voetnoot1). |
|



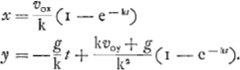
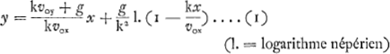
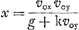 .... (2)
.... (2)