Oeuvres complètes. Tome XXII. Supplément à la correspondance. Varia. Biographie. Catalogue de vente
(1950)–Christiaan Huygens–
[pagina 343]
| ||||||||||
[pagina 345]
| ||||||||||
Deuxième partie.
| ||||||||||
[pagina 346]
| ||||||||||
Pressio venti cum prorae planum velo aequatur resistit pressioni aquae cum aqua habet celeritatem 1/29 celeritatis venti respectu veli. Nunc si prora sit tantum 1/10 prioris, celeritas aquae multo major in eam requiretur quam 1/29 celeritatis venti respectu veli. nam illa tantum resisteret decimae parti pressionis venti. Debet ergo aqua talem habere celeritatem quae faciat decuplum pressionis quam faceret habens 1/29 celeritatis venti. Non tamen debet habere 10/29 celeritatis respectivè venti sed mediam inter 10/29 et 1/29 hoc est 1/29 √10 ejus celeritatis, quia pressiones sunt ut celeritatum quadrata. Ergo si x sit celeritas quaesita navis, c ∞ 10, b ∞ 841, fit celeritatem resp. celeritas respectiva venti in velum aquae in proram 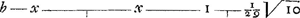 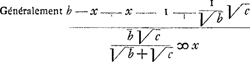 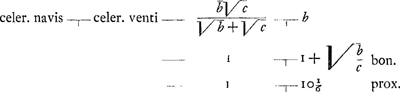 Ergo hic minor celeritas navis quam 1/10 celeritatis venti. Etiamsi c ∞ 841, hoc est si prora tantum 1/841 habeat resistentiae in aqua ejus quam haberet toti velo aequalis ac plana ac tota aquae occurrens, tamen tantum dimidia fiet celeritas navis ad celeritatem venti. § 12 (feuille collée dans le Man. I entre les f. 68 et 69). Pressio venti euntis secundum directionem CH in superficiem perpendicularem oppositam, ad pressionem versus L in superficiem obliquam BA eandem venti portionem excipientem, rationem habet compositam ex CH ad CD, et HE ad EF. hoc est eam quam qu. CH ad qu. CD, hoc est quam qu. AB ad qu. BKGa naar voetnoot1). Ponatur enim ventum esse quasi fluxum corpusculorum, quae dum feruntur secundum directionem CH, majorem celeritatem habent respectu superficiei KB, quam BA, quanto longior est CH quam CD perpend. CH, ut facile intelligitur. Quare tanto quoque validius pellunt superficiem KB ut cedat secundum directionem CHL, quam superficiem BA ut cedat secundum directionem sibi perpendicularem HE. Jam ut inveniamus quomodo se habeat vis qua impellitur planum BA secundum HL ad vim qua uti diximus impellitur secundum HE, oportet fingere fila tria CH, HE, HG quibus | ||||||||||
[pagina 347]
| ||||||||||
planum BA distineatur, quorum HG infinite longum sit, quod facit ut tantum in linea HL moveri possit planum AB; filum vero HE trahere putandum vi quanta diximus impelli planum idem secundum HE. Quaeritur vero quanta vi tendatur filum tertium HC comparata cum vi trahente secundum HE. Hoc enim ostendet mensuram conatus
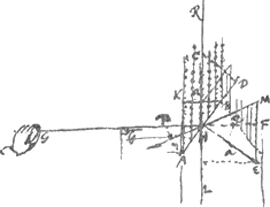 eundi secundum HL. Est autem inter illas vires ea ratio quae EF ad EH, ut constat ex legibus mechanicis funium trahentium. Ergo cum jam sit vis pellens KB secundum HL, ad vim pellentem planum BA secundum HC, sicut CH ad CD; vis autem haec sit ad vim pellentem BA secundum HL ut HE ad EF, hoc est ut HC ad CD, erit ergo vis pellens KB secundum HL ad vim pellentem BA secundum HL, ut quadr. CH ad quadr. CD, hoc est ut qu. BA ad qu. BK. quod erat demonstrandum. Quaenam ratio vis pellentis planum PQ ∞ AB, per HL, ad vim pellentem AB per HF. Ea componitur ex ratione PQ sive AB ad BK, hoc est ex HC ad CD, et rursus ex HC ad CD, et ex EH ad HF sive ex CH ad HD.
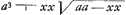 .
Cum a3 semper idem, debet esse xx .
Cum a3 semper idem, debet esse xx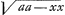 ∞ m. maximo si velim invenire qua inclinatione veli BA validissimè trahat secundum GPF. ∞ m. maximo si velim invenire qua inclinatione veli BA validissimè trahat secundum GPF.
 Voyez cette formule aussi dans la note 13 de la p. 530 du T.X. Sed si quis dicat ita positum velum in navi secundum GF pergente ommum maximè eam impellere, spirante vento secundum CHL, fallitur. Hic enim in computationem | ||||||||||
[pagina 348]
| ||||||||||
venire debet quanta fit aquae resistentia quae navem remoratur. Nam si ex. gr. nulla sit aquae resistentia, non poterit navis, ita posito velo, celerius ferri per HF quam ventus ipse per CH, quia ea celeritate incidens velum effugit omnem venti impulsum ut facile intelligitur. At si augeatur angulus inclinationis CHD, ut in CHM, pellet semper ventus velum, donec ejus celeritas per HF sit ad celeritatem venti ut HF ad FM perpend. sublatâ nempe ut ante aquae et alia quavis resistentia. Etsi enim exigua vi pellat secundum HF, pellit tamen continue, et proinde accelerat navis motum, quoad amplius non impellat. Ergo in navi quae magnam aquae resistentiam patitur, minor faciendus angulus quam in ea quae minorem patitur.
§ 13. Man. H, p. 186Ga naar voetnoot2). Puisque double vitesse de l'air ou de l'eau, contre un mesme plan, fait pression quadruple, comme on trouve par experience, et qu'alors il y a deux fois plus de particules qui frappent, et chacune avec deux fois plus de vitesse, il s'ensuit que le nombre simple de particules, avec double vitesse feroit pression double seulement. Tellement qu'il est certain que des mesmes particules la pression contre un plan est comme leurs vitesses a l'egard de ce plan.
§ 14. Man. H, p. 188. 10 Jan. 93. L'angle du vent et de la quille ABC estant donnè, trouver la position de la voile BD, qui fasse le plus avancer le vaisseau dans sa route. 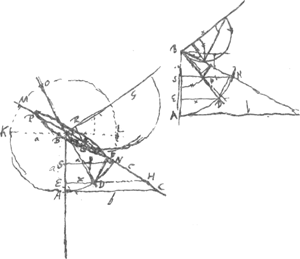 AB ventus. Pressio venti in KL ad pressionem venti in velum DO per BG perpend. | ||||||||||
[pagina 349]
| ||||||||||
sicut qu. BL ad qu. ED. Pressio ista in DO est ad pressionem quam inde sentit navis PF ad pergendum per BC ut BD ad DF: quae eadem ac QB ad BR. En marge: on ne considere point la derive. 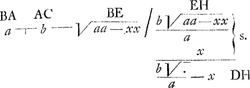 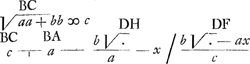 Ergo pressio venti in KL ad pressionem qua cogitur navis secundum BC habet rationem compositam ex aa 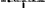 xx et xx et 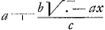 , hoc est , hoc est 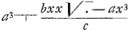 . .
Maxima autem pressio per maximum spatium navem protrudit. Quodsi ergo celeritatem puppis per datam PBH directionem hoc positu veli velimus maximum esse quae possit, oportet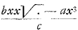 esse maximum....Ergo et esse maximum....Ergo et 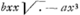 debet esse maximum, quia c est data ∞ debet esse maximum, quia c est data ∞ 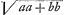 .
Sit ergo bxx .
Sit ergo bxx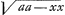 -ax3 ∞ s4. -ax3 ∞ s4.
Etc. La recherche du maximum, d'après la méthode de Hudde, conduit - nous ne publions pas ici le calcul, quisque nous l'avons déjà fait dans l'Appendice No. 2827 de la p. 532 du T. X - à la formule 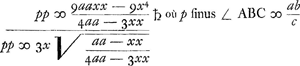 Il faut remarquer que dans ce calcul, autrement que dans les §§ 10 et 11 qui précèdent, la vitesse du vent est supposée assez grande pour que celle du vaisseau puisse être négligée en comparaison avec elle, de sorte que la vitesse du vent par rapport au vaisseau est considérée comme une grandeur donnée invariable. § 15. Chartae mechanicae f. 112, feuille détachée, remplie de calculs, que KortewegGa naar voetnoot3) dit avoir été collée dans le Man. F; mais c'est en vérité à notre § 14 emprunté au Man. H qu'elle se rattache. | ||||||||||
[pagina 350]
| ||||||||||
Posito angulo ABC carenae et venti, plurimum insurgetur in ventumGa naar voetnoot4), si ita velum statuatur ut maximam celeritatem navis acquirat. Haec vero veli constitutio ex illo angulo posito invenitur. qua itaque inventa, quaeratur ex formula Ω, quantitas in ventum confectaGa naar voetnoot4). Formula ΩGa naar voetnoot5) est x/c .c est secans ad sinum p. aa/c est sinus compl. ad sinum p. Ω ∞ maximum. .c est secans ad sinum p. aa/c est sinus compl. ad sinum p. Ω ∞ maximum.
VelGa naar voetnoot6) ex singulis hypothesibus sinus anguli veli et venti, inveniatur sinus anguli venti et carenae, p, ex regula ♄; ponendo x cognitam, p quaesitam. § 16. Man. H, p. 190 (comparez la note 14 de la p. 530 du T. X). Invento xx et x per datas a, b, c, fiat tabula, quae ad singulas c seu secantes anguli quem facit linea venti cum carina, ostendat sinum x, anguli optimi carinae et veli...Et ex singulis computato spatio ex formula Ω, notetur quodnam fiet maximum. Sic habebitur et navis et veli positio utilissima, ad insurgendum contra ventum, quod dicunt gagner au vent. Vel brevius possumus ex singulis hypothesibus sinus veli et venti, invenire sinus venti et carinae, ex regula ♄ pag. 188. ponendo x cognitam, p quaesitam...Tum ex a, c, b, vel p et x computetur longitudo seu spatium Ω. Et fiat tabula, ubi apparebit quaenam Ω sit maxima. D'aprês le § 14 la ‘pressio venti’ dans le sens de la route, et de la longueur, du vaisseau (ces deux sens étant considérés comme identiques, puisque la dérive, comme Huygens le dit lui-même, n'a pas été considérée) est bx2√a2-x2-ax3/c, dont la composante dans le sens de ce que l'on ‘gagne au vent’ est a/c2(bx2√a2-x2-ax3). Les facteurs a, b, et c étant constants, l'une ou l'autre de ces expressions doit être maximale. Posant ϕ=a/c2(bx√a2-x2-ax3), l'expression Ω de Huygens, eu égard à la formule ♄, prend la forme 1/√c√ϕ. C'est la vitesse - proportionnelle à la racine carrée de la ‘pressio’, égale à la résistance de l'eau: les résistances, on l'a vu plus haut, étant jugées proportionnelles aux carrés des vitesses - qui elle aussi doit être maximale. § 17. Même endroit. L'angle du vent et de la voile BAI estant de 45 degrez, trouver la situation de la quille AG pour gagner au vent le plus qu'il se peut. BA estant la ligne du vent, a qui AH est perpendiculaire, si le vaisseau en certain | ||||||||||
[pagina 351]
| ||||||||||
temps parcourt AG, la ligne GH parallele au vent est ce qu'il gagne au vent dans ce tempsGa naar voetnoot7). 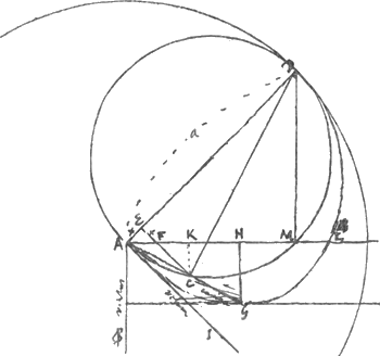 AG est moiene proportionelle entre AC, AD. AL moiene proportionelle entre AM, AD, &c.Ga naar voetnoot8). AGLD est la courbe qui fait voir combien de chemin fait le vaisseau dans les differentes positions de sa quille, la voîle demeurant en AI, inclinee sur AB de 45 degrez. Il faut chercher cette meilleure situation du vaisseau dans toutes les positions de la voile au vent, pour en conclure comment le vaisseau et la voile doivent estre situez pour gagner le plus au vent. § 18. Man. H, p. 189. Cette Pièce peut être considerée comme un avant-projet de l'article de Huygens de septembre 1693 dans la ‘Biblothèque Universelle et Historique’, T. X, p. 525. | ||||||||||
[pagina 352]
| ||||||||||
Quand un corps tombe par l'air, ou chemine dans l'eau, d'un mouvement egal; la force qui le pousse est egale à la resistence que luy font l'air ou l'eau. Autrement sa vitesse croitroit ou diminueroit. L'autheur de la manoeuvre des vaisseaux - imprimè en 1689 de l'expres commandement de Sa MajestèGa naar voetnoot9) - dit fort bien que dans le vaisseau HM la voile estant selon DC, il seroit poussè par BG, perpend. sur DC, s'il fendoit l'eau de tous costez avec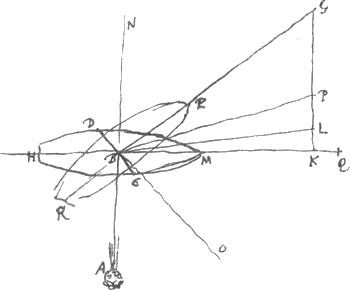 egale facilitè. Qu'il avanceroit de pointe de la quantitè BG, et de costè de la quantitè KG. Mais quand il dit que si comme la facilitè de fendre l'eau avec sa pointe, a celle qu'il a de la fendre avec son costè, ainsi l'on fait GK à KL, le vaisseau ira par BL, dans le mesme temps qu'il seroit allè autrement par BG, il se trompe. Outre cela il raisonne comme si le vaisseau n'estoit poussè que par le vent qui donne contre la voile DC. Mais le corps du vaisseau recevant l'impulsion du vent qui le pousse directement par BN perpendiculaire à la quille, ou a peu pres, et point du tout par BK, cela doit augmenter considerablement la derive, et faire le plus d'effet lors que le vent est perpendiculaire sur la quille, comme icy AB, et moins quand il souffle par OB. De sorte qu'il seroit besoin d'essaier la quantitè de la derive dans les diverses variations du vent, à l'egard de la quille. Et par là toute cette theorie de l'autheur deviendroit incertaine | ||||||||||
[pagina 353]
| ||||||||||
outre le paralogisme. Mais ce qu'il y a de vray et de certain, c'est de determiner, lors que le vent et la position de la quille (qui convient avec la route lors qu'on considere la derive comme rien) sont donnez, quelle situation de la voile est la plus avantageuse. Car quelle que soit la derive, l'on aura par là la plus grande vitesse pour le mouvement selon BK, qui composè avec celuy de la derive, menera le vaisseau selon BL ou BP. L'autheur n'a pas scu donner cette determination de la voile, pour ij avoir voulu comprendre l'effet de la derive. Il trouve fort bien la meilleure position du gouvernail a l'egard de la quille, pour faire tourner le vaisseau le plus promptement. Et cet angle qu'ils doivent faire ensemble pour cela, est celuy dont le sinus est √⅔aa quand a est le raion. Qui est le mesme que celuy que doit faire la voile avec la ligne du vent, pour aller le plus viste à moitiè vent, c'est a dire dans le cas que la ligne du vent est perpendiculaire sur la quille et sur la ligne de la route, car je ne conte point la derive. Car si AB est la quille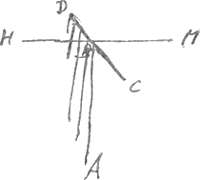 et BD le gouvernail, il faut s'imaginer que le cours de l'eau, parallele a la quille donne contre BD, et pousse par là le bout du vaisseau B, par BM perpend. sur AB. Mais si AB est la ligne du vent qui donne contre la voile DBC, (placee sur la quille, que je suppose à cet heure HM), pour faire avancer le long de la mesme HM; il paroit que la situation de la voile CD et du gouvernail BD, doivent estre les mesmes, pour estre les plus avantageuses. Sa theorie seroit vraie si les resistences de l'eau estoient comme les vitesses du vaisseau, mais ces resistences sont comme les quarrez des vitesses. Si le vaisseau HM passoit en mesme temps la ligne BK, que le mesme vaisseau RP parcourt la ligne BG, la resistence de l'eau dans le premier cours, à sa resistence dans l'autre cours, seroit comme le quarrè de BK au quarrè de BG, et il faudroit que la pression que luy cause le vent vers BK fust aussi à la pression qu'il luy cause vers BG comme les dites resistances, c'est a dire comme le quarrè BK au qu. BG. Mais les pressions sont comme la ligne BK à la ligne BG, la voile estant CD, située de mesme a l'egard du vent dans les deux routes. Le vaisseau ne parcourt donc pas en des temps egaux les lignes BG BK. Mais si on prolonge BK en Q, de sorte que BQ soit moiene proportionelle entre BG, BK: le vaisseau RP et HM poussè par la mesme situation de voile DC parcourra en des temps egaux les lignes BG, BQ. Parce que les resistences aussi bien que les pressions dans [ce cas seront comme] les lignes BG BK. On trouve à la p. 107 du Man. I (comparez la note 2 de la p. 654 du T. X) sous le titre ‘Convictio Renaudij’ la minute d'une partie de la ‘Replique de Mr. Huguens [de juin 1694] à la Reponse de Mr. Renau [de janvier 1694 à l'article de Huygens de septembre 1693]’. |
|


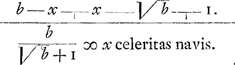
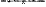 1
1