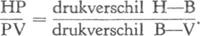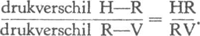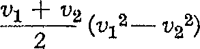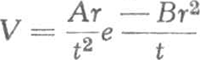De natuurkunde van 't vrije veld. Deel III
(1940)–Marcel Minnaert–Rust en beweging
[pagina 236]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
141. De aneroïde.Geen instrument lijkt zo eenvoudig af te lezen als de aneroïdebarometer: het is voldoende zachtjes tegen het glas te tikken en op de blauwe naald te letten. Helaas zijn de correcties die men aan de aflezing moet aanbrengen nogal onzeker. Men corrigeert voor de hoogte boven de zeespiegel; de temperatuurinvloed, die afwijkingen tot wel 4 mm kan veroorzaken, is helaas zó onregelmatig dat er niet voor te corrigeren valt. Men moet de aneroïde dus vooral gebruiken voor het onderzoek van snelle veranderingen van de luchtdruk, niet voor het bepalen van het absolute bedrag ervan. Bij het tikken ziet men meestal de blauwe naald een weinig verspringen, en nu hoort men wel eens beweren dat dit de richtting is waarin de luchtdruk net aan 't veranderen is. Een statistisch onderzoek heeft echter aangetoond dat dit slechts in 62% der gevallen uitkomt, althans als men drie maal daags waarneemtGa naar voetnoot1). Blijkbaar vertoont de luchtdruk teveel onregelmatige kleine schommelingen. Neem een aneroïde barometer zoals in onze huiskamer hangt, en vergelijk zijn aanwijzing in de kelder en op de zolder: het verschil is duidelijk merkbaar. Bestijg een hoge toren en lees telkens na 100 treden de stand van de naald af, zachtjes tikkend vóór elke aflezing. De druk neemt geleidelijk af; uit de hoogte van de toren vindt u dat dit afnemen ongeveer 1 mm per 10 meter bedraagt. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 237]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
142. De kwikbarometer.Ga naar voetnoot1)Soms heeft men moeite met het aflezen van de juiste stand van de kwikzuil. Houd dan achter de buis een papiertje, waarvan de bovenste helft zwart is, de onderste wit. De meniskus kaatst het zwart terug en schijnt donker op heldere grond. Het is van belang, te kunnen controleren of de ruimte boven het kwik wel geheel luchtledig is. Houd daartoe de barometer een weinig schuin: het kwik stijgt in de buis en moet nu met een korte, scherpe tik tegen het eind der buis aanslaan. Aan de aflezing zijn de volgende correcties aan te brengen.
De correcties 4 en 5 zijn eens en vooral te bepalen en telkens als geheel aan te brengen. Een algemene contrôle verkrijgen we door de barometer af te lezen op het ogenblik der ‘termijnwaarneming’ van een onzer meteorologische stations, dus 's ochtends te 8 uur; en dan bij ontvangst van het weerkaartje de waarde die we afgelezen hadden te vergelijken met wat onder het kaartje opgegeven staat. De moeilijkheid is echter, dat we in 't algemeen niet wonen | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 238]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
bij een der hoofdstations (De Bilt, Vlissingen, Maastricht, den
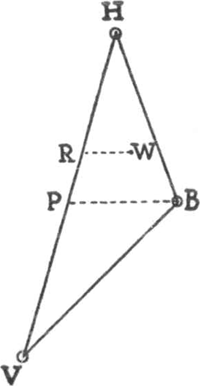 Fig. 115. Het vergelijken van een barometer met de opgaven van drie meteorologische hoofdstations.
Helder, Groningen), zodat we meestal moeten ‘interpoleren’. Dat gaat het best zóGa naar voetnoot1). Kies een dag waarop de drukking vrij gelijkmatig over Nederland verdeeld is, of waarop de lijnen van gelijke drukking ongeveer van onze woonplaats naar een der hoofdstations lopen. Stel we bevinden ons binnen de driehoek Den Helder-De Bilt-Vlissingen, en de volgorde dezer stations zij tevens die der afnemende barometerdrukkingen (fig. 115). Op de lijn VH moet er een punt P zijn waar de drukking dezelfde is als in B, waarschijnlijk zó gelegen dat | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
143. Waterbarometer. (fig. 116).Neem een glazen kolf van 1 liter inhoud, doe er wat water in,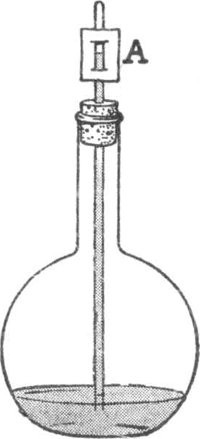 Fig. 116. Eenvoudige waterbarometer.
stop hem met een gummistop, waardoor een glazen buis tot bijna op de bodem daalt. Blaas even in het buisje zodat enkele bellen door het water borrelen: de druk in de kolf is dan een weinig toegenomen, en als u ophoudt te blazen stijgt het water, bijvoorbeeld tot A. Iedere verandering in de dampkringsdrukking zal nu het peil van het water in het buisje doen stijgen of dalen. Hoeveel? Het toestel is veel gevoeliger dan een gewone barometer, des te meer naarmate de kolf groter is en het buisje smaller. Het bezwaar is alleen dat het temperatuurveranderingen op dezelfde wijze aangeeft als drukveranderingen; maar hier kunnen we enigszins aan tegemoet komen, door de kolf in een kistje te zetten, en hem geheel in pakwatten of oude kranten in te pakken, terwijl alleen het boveneind van het buisje erboven uitsteekt. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 239]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Ga met de waterbarometer naar een andere verdieping: het water daalt of stijgt verscheidene millimeters. Op een toren bedraagt het hoogteverschil wel 10 cm. Bij de ‘mondbarometer’ kan het reservoir in de mond onder de tong gehouden worden, zodat men zeker is van een konstante temperatuur. Het toestelletje is gemakkelijk te maken en kan voor barometrische hoogtemeting goed gebruikt worden (Ann. Phys. 1902). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
144. Variometer. (fig. 117).Neem een glazen kolf van 2 1, die geen water bevat, en die u desnoods open aan de lucht laat staan tot hij droog geworden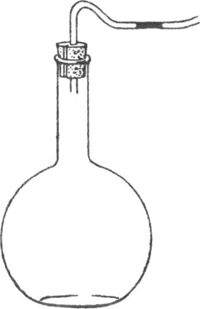 Fig. 117. Eenvoudige variometer.
is. Stop hem met een kurk, waardoor een glazen buisje gaat van slechts 3 mm inwendige diameter, en dat omgebogen is zoals uit fig. 117 te zien is. Nu moet ervoor gezorgd worden dat de kurk een heel klein lek vertoont: we snijden een zeer smal gleufje in de zijwand van de kurk, zo ondiep, dat bij sterk aandrukken de sluiting vrijwel luchtdicht is, bij minder aandrukken een weinig lucht laat doorlekken. Breng een druppel benzol of xylol in het buisje - onze variometer is klaar. We noemen hem een ‘variometer’, omdat hij de veranderingen van de luchtdruk aanwijst. Bij buiig, stormachtig weder is de druppel geen ogenblik in rust; hij verschuift over millimeters, zelfs centimeters. Het is een buitengewoon merkwaardig schouwspel om met dit instrument het voorbijtrekken van een bui te volgen. Een deur die men opent of sluit geeft zeer plotselinge verplaatsingen. Daarentegen wordt een geleidelijk toenemen of afnemen van de luchtdruk niet opgetekend, omdat de overdruk zich dan intijds vereffenen kan door langs het lek weg te stromen. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
145. Barometerdruk in vuurtorens.De geweldige stormwinden die soms om de vuurtoren gieren, veroorzaken een overdruk, een stuwing aan de loefzijde, een onderdruk aan de lijzijde. Zet men een raam open naar de ene of naar de andere dezer twee kanten, dan kan men de drukverandering zeer duidelijk merken aan de aneroide-barometer in de toren. Zijn alle ramen en deuren dicht, dan stelt zich de | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 240]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
drukking door reten en kieren toch in op de gemiddelde drukking van de lucht in de omgeving, en die ligt iets lager dan de normale druk. Bij een bepaalde toren werd gemeten:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
146. Natuurverschijnselen bij veranderende barometerdruk.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 241]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
147. Het oor als barometer.Ga naar voetnoot4)Snelle drukveranderingen voelt men door een eigenaardige spanning in het trommelvlies van het oor; door te slikken herstelt men dan gemakkelijk langs de buis van Eustachius de gelijkheid van druk binnen en buiten. Sommige mensen zijn erg gevoelig voor dit effekt, waarschijnlijk omdat de buis van Eustachius bij hen min of meer verstopt is. In de eerste der hierna opgesomde gevallen is de drukverandering door iedereen waarneembaar; in de volgende is ze toenemend moeilijk op te merken. In een vliegtuig, vooral bij de daling. In een lift, vooral in de snelle liften van kolenmijnen of torenhuizen. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 242]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Als de trein een tunnel binnenrijdt of eruit komt. Als de deuren van een kamer dicht zijn, en men ineens het raam opent waarop de stormwind staat. Als men met alle kracht de kamerdeur plotseling opent of sluit. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
148. De luchtweerstand van een bol.Op een mooie Zaterdagnamiddag, in 't voorjaar, hebben we boodschappen in de stad gedaan en keren terug met twee van die leuke kinderballonnetjes die men af en toe als geschenk krijgt in de grote warenhuizen; we hebben ze zo goed mogelijk bolvormig gekozen. - We beginnen met een ballonnetje te meten en te wegen. Het is een beetje langwerpig, de grote as is 35 cm lang, dwars daarop heeft het een middellijn van 30 cm. Aangezien de inhoud van een bol 4/3πr3 is, schatten we hier: 4/3π.175×15×15=16·600 cm3 = 16,6 liter. Het gewicht is negatief, want het ballonnetje heeft stijgkracht; als ik er 15 g aan bind blijft het bijna zweven in de lucht, daalt heel langzaam; met 20 g eraan bevestigd weegt het geheel 5,5 g, de ballon had dus een stijgkracht van 20 - 5,5 = 145 g. Het omhulsel van een ballonnetje waar al het gas uit ontsnapt is, blijkt 3 g te wegen; het gas alleen had dus een stijgkracht van 145+3 = 175 g. Als s het gewicht van een liter gas voorstelt, moet 16,6(1,293-s) = 17,5 dus s = 0,23 g per liter. Hieruit volgt met stelligheid dat het ballonnetje met waterstof gevuld was; maar blijkbaar was er door diffusie al wat lucht bijgekomen. Als men zulk een ballonnetje zou loslaten, zou het eerst langzaam, dan sneller stijgen, tot het een bepaalde grenssnelheid bereikt heeft, waarbij de wrijving tegen de lucht net even groot is als de stijgkracht. Doordat het ballonnetje echter zo groot is en de stijgkracht betrekkelijk gering, wordt die grenssnelheid in de praktijk bijna onmiddellijk bereikt. We nemen de proef eerst in onze huiskamer, met het horloge in de hand, en bepalen in hoeveel tijd het ballonnetje van de vloer tot het plafond opstijgt. - Veel mooier gaat het echter buiten, als we een windstil plaatsje achter het huis kunnen vinden. Een draad dun naaigaren van 10 of 20 meter lengte wordt met zijn ene uiteinde aan een zware steen vastgemaakt, met zijn andere uiteinde aan het ballonnetje; wees niet bang voor verwarren van de draad, laat hem eenvoudig op een hoopje op de grond liggen zoals hij zichzelf legt, dan komt het best terecht. Dan weer de ballon oplaten en nauwkeurig de tijd bepalen die verloopt tot hij over de volle lengte van de draad opgestegen | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 243]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
is. De proef kan nu herhaald worden nadat we bekende gewichtjes onder aan het ballonnetje hebben bevestigd. Zelfs kunnen we een deel van het gas uitlaten, om de invloed van de afmetingen
 Fig. 118. Het oplaten van luchtballonnetjes om de weerstand van een bol te onderzoeken.
te kunnen onderzoeken; het is duidelijk dat hetgeen er op aankomt vooral de doorsnede van het ballonnetje in een horizontaal vlak is, en die is weer het eenvoudigst vast te leggen door met | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 244]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
een touwtje de omtrek van de horizontale doorsnede te meten, daaruit r, r2 en πr2 = S te berekenen. De weerstand S van een bol, die bij onze proeven gelijk is aan de stijgkracht, is evenredig met het oppervlak F van zijn doorsnede, met het kwadraat van zijn snelheid v, met het soortelijk gewicht γ van de vloeistof of het gas waarin hij beweegt (althans indien de omstandigheden niet àl te zeer worden gewijzigd). Men schrijft in de techniek gewoonlijk: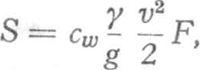 waarin alle grootheden in de technische eenheden meter, sekunde kilogram-kracht uitgedrukt zijn. Dan wordt in gewone omstandigheden γ = 1,225 kg/m3, γ/g = 0,125 = ⅛. Dus 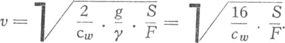 Hier volgt een deel van de uitkomsten die ik verkreeg toen ik de proef het eerst uitvoerde.
't Gemiddelde van alle proeven gaf de formule: S = 0,66 v2F/16, wanneer v in m/sec, S in kg-gewicht, F in m2 uitgedrukt wordt. De vrij goed constante waarde die we voor c krijgen, bewijst dat inderdaad de weerstand ongeveer evenredig is met het kwadraat der snelheid (bij veel groter snelheden komen er complicaties). De hier gevonden formule zal ons later dienen als we een loodsballon oplaten en de snelheid van de wind in hoge lagen berekenen (§ 160). Om onze formule ook te toetsen voor veel kleinere bollen en de invloed van de afmetingen te onderzoeken, moeten we een | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 245]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
geheel ander soort proef nemen. Koop een ping-pong balletje, zo'n heel licht en effen celluloid dingetje, en bevestig er een draadje aan met een weinig kleefwas. Spring nu op de fiets, rijd langs een goed beschutte windstille weg, en houd de draad als slinger iets vóór u en naast u, zodat het balletje de volle luchtstroom krijgt. Het wijkt achteruit en de draad gaat schuin hangen. Bij een snelheid van 15 km per uur hing de slinger onder een hoek die ik op 8o schatte, bij 20 km per uur werd de hoek wel 20o
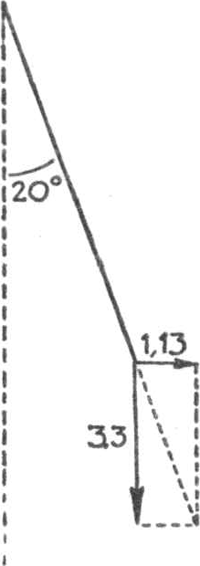 Fig. 119.
(fig. 119). Het balletje bleek 3,3 gram te wegen; de wrijving was dus achtereenvolgens 3,3 . tg 8o = 0,46 g-gew. en 3,3 . tg 20o = 1,20 g-gew. bij snelheden van 4,2 m/sec en 5,5 m/sec. Aangezien het oppervlak der dwarse doorsnede 11,1 cm2 bedroeg, is de constante cw van onze formule 0,37 of 0,57, gemiddeld 0,47. Dus geheel van dezelfde orde als met ons ballonnetje bepaald was! De weerstand van een bol is dus inderdaad evenredig met het oppervlak van zijn doorsnede. Volgens de beste officiële metingen moest cw = 0,45 zijn. De overeenstemming van onze ruwe metingen (0,66 en 0,47) met het zorgvuldig in de windtunnel bepaalde getal is niet onbevredigend. Dat wij iets kleiner snelheden, dus iets groter luchtweerstand vinden, is wellicht te wijten aan de oneffenheden op onze ballen, waardoor wervels veroorzaakt worden, en aan de onvoldoende wervelvrijheid van de lucht waarin we werken. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
149. Vallende lichamen met weinig luchtweerstand.Om de valbeweging te onderzoeken volgen we 't voorbeeld van Galilei en maken gebruik van een uitzichtstoren of van 't balkon van een hoog gebouw. Neem een lang touw, en bevestig daaraan stukjes lood of ijzer of wilde kastanjes, op afstanden van 4 m van elkaar. Neem een tweede touw, en bevestig daaraan dergelijke gewichtjes op afstanden 0; 1,25 m; 5 m; 11,25 m van het uiteinde (dus 1,25; 3,75; 6,25 m van elkaar). - Begeef u nu op het balkon en laat het eerste touw zo hangen, dat het onderste gewichtje net de grond raakt. Als u nu het touw ineens loslaat, hoort u de tikken van de vallende gewichtjes, en wel met steeds korter wordende tussenruimten: vallende voorwerpen krijgen dus een geleidelijk toenemende snelheid. Herhaal de proef met het tweede touw: ditmaal zijn de tussenruimten tussen de tikken | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 246]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
gelijk; in tijdsruimten 1, 2, 3, .... zijn dus de afgelegde wegen 1,25 m; 4 × 1,25 m; 9 × 1,25 m; .... Doe de laatste proef nog eens, maar tel daarbij zo nauwkeurig mogelijk sekunden, beginnend met 0 op het ogenblik dat u het touw loslaat. De tikken blijken nu precies met tussentijden van ½ sekunde op elkaar te volgen. Een vrij vallend voorwerp legt dus in de eerste sekunde een weg af van 5 meter; na t sekunden is de afgelegde weg (in meters) ongeveer: s = 5t2. Gooi met alle kracht een kei recht omhoog, en laat een helper nauwkeurig bepalen hoeveel sekunden en tienden van een sekunde verlopen eer de kei weer op de grond terugvalt (§ 10). Hij houdt het horloge aan zijn oor, en begint te tellen op het preciese ogenblik, waarop de steen wegvliegt (0 1 2 3 4 1 1 2 3 4 2 ... ): een prachtige oefening om korte tijden nauwkeurig te leren bepalen! Herhaal de proef enkele malen en neem het gemiddelde t van de uitkomsten. Hieruit volgt nu vooreerst, met welke snelheid v0 de steen omhooggegooid is: uit hoofde van deze worp zou de steen in een tijd t opgestegen zijn tot een hoogte v0t; maar tevens is de steen gevallen over de afstand ½gt2. Als de steen terug op de grond komt is v0t = ½gt2, dus v0 = gt/2. Voor mijzelf is t = 3,0 sec, dus v0 = 15 m/sec. - De steen stijgt zolang, tot de valsnelheid net gelijk is geworden aan de worpsnelheid, dus tot gtm = v0; hieruit volgt: tm = v0/g = t/2. De steen gebruikt dus evenveel tijd om zijn hoogste punt te bereiken als om terug te vallen. - Tenslotte kunnen we ook de bereikte hoogte vinden: v0tm - ½gtm2 = gtm2 - ½gtm2 = ½gtm2. In ons geval komt er: 11,0 meter. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
150. Snelheid van vallende regendruppels.Ga naar voetnoot1)Als het regent terwijl we in de trein zitten, kunnen we mooi de regendruppels in evenwijdige schuine strepen langs de ruiten zien lopen. Die druppels zijn van zó hoog gevallen, dat ze al lang een eenparige snelheid hebben gekregen, evenals ons ballonnetje, vallende sneeuwvlokken, of luchtbelletjes die in 't water opstijgen. De eindsnelheid kunnen we nu bepalen uit de richting der regenstrepen (fig. 120): de druppel verplaatst zich op de ruit | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 247]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
in vertikale richting AB door zijn valbeweging, in horizontale
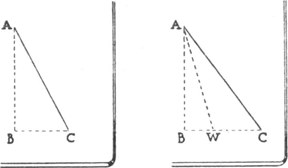 Fig. 120. Sporen van vallende regendruppels op de ruiten van een trein. Links: bij windstille lucht. Rechts: bij wind.
richting BC doordat de trein een eigen snelheid heeft; de regenstreep is de resultante van het snelheidsparallelogram. Hieruit volgt:  . De snelheid van een trein is van de orde van 25 m/sec; voor de regendruppels vindt men snelheden van enige m/sec. Tot hiertoe hebben we aangenomen dat de regendruppel vertikaal viel; mocht echter reeds een helling van de regenstrepen waar te nemen zijn eer de trein in beweging gekomen is, dan krijgen we:  . Opvallend is het verschil tussen regenstrepen van grote en van kleine druppels; deze laatste hellen veel meer, blijkbaar vallen ze met een aanzienlijk kleinere snelheid dan de grote. Laten we eens een stoute sprong wagen, en uit onze waarnemingen met het loodsballonnetje en het ping-pong balletje afleiden hoe snel een druppel van gegeven afmetingen vallen moet. De stijgkracht van het ballonnetje is hier te vervangen door het gewicht van de druppel. We hadden (§ 148):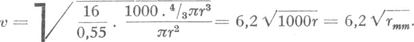 Uit proeven is gebleken dat deze wet inderdaad heel aardig klopt, zolang de druppels niet al te klein worden. Een druppel van 2 mm middellijn valt dus met een snelheid van 6 m per sekunde. Het is eigenlijk wel merkwaardig dat die regenstrepen zo mooi recht zijn. Ongetwijfeld vermindert de snelheid van de druppel tengevolge van de wrijving, maar neemt hij ook iets over van de snelheid van de trein; tevens wordt hij kleiner; en dan is er | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 248]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
nog de invloed van de luchtstromen om de trein. In elk geval blijkt de resulterende baan praktisch recht, althans over het kleine stukje waarover men die baan opgetekend ziet. Wel kan men opmerken hoe een druppel die een regenstreep heeft beschreven, dikwijls aan het eind van zijn baan, als hij tot stilstand gekomen is, een paar andere druppels opneemt en in een bijna vertikale richting naar beneden rolt; hier heeft de oorspronkelijke valsnelheid bijna geen invloed meer. Om de helling der regenstrepen te bepalen is er echter gelukkig een andere methode, die aan geen enkele bedenking onderhevig is. Let eens op de arcering die het gehele landschap overdekt: zij ook verandert van richting zodra de trein in beweging komt; en in dit geval weten we met zekerheid dat we de valsnelheid bepalen, buiten elke complicatie om van wrijving tegen de ruiten. U zult bevinden dat ze zowel bij stilstand als bij beweging van de trein vrijwel evenwijdig gericht is aan de regenstrepen die zich op de ruit aftekenen. Dit bewijst dat de storingen die wij vreesden toch maar een geringe invloed op het verschijnsel hebben. De direkte waarneming der regenarcering door het open raampje geeft ons daarenboven nog de mogelijkheid, de strepen over een grote afstand te overzien, en waar te nemen dat deze strepen geheel recht zijn; waaruit volgt dat de druppels werkelijk een eindsnelheid hebben bereikt, en niet meer sneller en sneller vallen door de invloed der zwaartekracht. Let ook op de regenarcering terwijl u in een tram rijdt, in een auto, op de fiets. Nog eenvoudiger: bemerk hoe die richting verandert, al naarmate u loopt of stilstaat (natuurlijk altijd dwars op uw beweging kijken, dus naar rechts of naar links!). Of beweeg het hoofd snel naar rechts en naar links: u ziet de helling der regenstrepen bij iedere zwaai van het hoofd afwisselend groter en kleiner worden! Al deze waarnemingen bewijzen duidelijk dat de regenstrepen eenvoudig snel vallende druppels zijn, die op het oog de indruk van lijnen maken; maar dat het helemaal geen straaltjes water zijn zoals u misschien gedacht had. Want al loop ik nog zo hard, of al zit ik in een trein, nooit zou een vertikaal hangend touw mij daardoor schuin schijnen! U kunt zich daar rechtstreeks van overtuigen, door vlak naast een huis te gaan staan en bijna vertikaal omhoog te kijken. Tegen de donkere achtergrond van dak of dakgoot of tegen de heldere hemel ziet u de druppels vallen, en doordat u bijna in hun valrichting kijkt, ziet u ze vertraagd: het zijn afzonderlijke heldere of donkere bolletjes, geen lijntjes. Het is leuk om op te merken | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 249]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
hoeveel kleine druppeltjes er naast de weinige grote vallen. Let ook op hoe een grote druppel die van de dakrand valt bijna altijd door een kleintje gevolgd wordt, soms door twee kleintjes; men ziet hoe de afstand tussen de grote en de daaropvolgende kleine druppel tijdens het vallen toeneemt, tengevolge van het verschil in luchtweerstand. Richt een camera met volle opening op een donkere muur of open deur. De camera is ingesteld op 3 meter. Als het regent maakt u enkele momentopnamen met 1/25 sekunde belichtingstijd. Ze vertonen de regen als streepjes, waarvan de lengte afhangt van de grootte van de druppels; uit de opname kan men het aantal druppels van elke verschillende snelheid bepalen, en dit met onze formule omrekenen in de straal der druppels. Is de camera niet zeer lichtsterk, dan moet men wachten tot de zon toevallig eens schijnt terwijl de regen valt en ze de druppels doet schitteren; het mooist is dit te zien tegen een donkere achtergrond, in een richting, die een kleine hoek maakt met de richting naar de zon. Het giet, het giet gestadig! Geen losse druppels meer; Maar vast en ijzerdradig, Rechtresemend en zeer ..... | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
151. Vallende sneeuwvlokken.Sneeuwvlokken vallen zo langzaam dat men ze gemakkelijk met het oog kan volgen; duidelijk kan men zien hoe ze met een mooie, eenparige beweging neerkomen. Dat ze zoveel langzamer vallen dan regendruppels is aan hun veel grotere luchtweerstand te wijten. Bij zeer rustig weer gaan we de snelheid bepalen waarmee de sneeuwvlokken dalen. Op het ogenblik dat we een bepaalde vlok de horizonlijn zien kruisen, beginnen we sekunden te tellen: 0, 1, 2, 3, .... en we letten op wanneer die vlok op de grond aankomt. Dit is in 't algemeen tussen twee tellen in; schat tiende delen van een sekunde (‘oog- en oormethode’). De valhoogte is gelijk aan de afstand van ons oog boven de grond. In een bepaald geval vond ik dat de vlokken gemiddeld een snelheid hadden van 0,75 m/sec. - Men kan ook een huis of een boom van bekende hoogte uitzoeken, en een vlok volgen die daar dicht tegenaan valt. Naar mijn ervaring vallen de grote vlokken merkbaar sneller | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 250]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
dan de kleine, men ziet ze vooruitsnellen; de verhouding der snelheden is bijvoorbeeld 1,3. Dat lijkt zeer begrijpelijk, want de luchtweerstand neemt toe met de tweede macht der afmetingen, het gewicht echter met de derde macht, zodat de invloed van de wrijving relatief kleiner wordt, de eindsnelheid dus groter. Andere waarnemers spreken dit nochtans tegen; Maille deelt mee, dat vlokken van 3 tot 4 cm grootte met een snelheid van 0,25 tot 0,35 m/sec vallen, vlokken van 1 cm met een snelheid van 0,80 m/sec. Dat kan alleen als de grote vlokken luchtiger gebouwd zijn dan de kleinere, wat natuurlijk bij bepaalde weersomstandigheden voorkomen kan. Een andere schrijverGa naar voetnoot1) bevestigt onze ervaring en geeft op: 1,80 m/sec voor vlokken van 2 cm; 1,10 m/sec voor vlokken van 5 mm. Ongetwijfeld zal ook de ‘natheid’ van de sneeuw een grote invloed op de valsnelheid hebben. - Bijna alle vlokken draaien terwijl ze vallen; ze zijn nooit geheel symmetrisch en werken dus altijd min of meer als een schroef. Denk aan vallende lindevruchtjes! Na het waarnemen van de dalende sneeuwvlokken ondergaat men een zeer sterke gezichtsbegoocheling: alle voorwerpen schijnen van beneden naar boven te bewegen! - Zie hiervoor I § 108. Als de sneeuw uit een wolk valt die 2000 m hoog is, hoelang doet zij er dan over voor ze beneden is? Hoever kan ze worden meegevoerd door wind van 8 m/sec eer ze de grond bereikt? We hebben de snelheid van regendruppels bepaald uit de sporen die ze achterlaten op de ruiten van een bewegende trein. Bij sneeuwvlokken is dat niet mogelijk; maar men kan wel van uit de trein naar buiten kijken en de richting waarnemen van de arcering waarmee de vallende vlokken het landschap bedekken. Men bevindt dat ze bijna horizontaal schijnen te bewegen. Inderdaad is hun valsnelheid zeer klein ten opzichte van de snelheid van de trein, en wel ongeveer 0,75/25 = 1/30; dat is niet goed meer te bepalen. Het lukt echter wel als men eenvoudig gaat lopen met een normale snelheid van 5 km/uur of 1,4 m/sec: de schijnbare valrichting is dan heel sterk verschillend van de ware. Als men 's avonds vóór in een auto zit, en door een bui van kleine sneeuwvlokjes rijdt, kan men een treffend schouwspel bijwonen. Het felle zoeklicht van de auto verlicht de vlokjes, en men ziet ze allemaal lichtlijntjes aftekenen die uitstralen | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 251]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
van een punt vlak vóór ons. De beweging van de auto is zó snel, dat ik ten opzichte daarvan de vlokken wel als in rust kan beschouwen; ik kan mij dus ook de auto stilstaand voorstellen, en alle vlokjes met grote snelheid horizontaal naar hem toe bewegend. En nu is het een bekend perspektivisch effekt, dat al die evenwijdige banen schijnen uit te stralen van een vluchtpunt in de verte, zoals spoorrails en telegraafdraden, en zoals vallende sterren die van een ‘radiant’ uitstralen. - Mocht de valsnelheid der sneeuwvlokken niet geheel te verwaarlozen zijn, dan zou ik mij al de relatieve snelheden moeten voorstellen als een weinig hellend ten opzichte van de horizontaal, zodat het uitstralingspunt niet op de gezichteinder, maar iets hoger ligt. Is daar iets van te bemerken? Bereken dan uit die hoogte de valsnelheid van de vlokken! | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
152. Vallend water.De ‘echoput’ te Hoog Soeren, bij Apeldoorn, is ongeveer 80 meter diep. Laat men er een schep water in vallen, dan horen we het plassen na 7 tot 8 sekunden. Het geluid heeft 0,2 sec nodig gehad om ons oor te bereiken (II § 3), het water doet dus ongeveer 7 sec over het vallen. Volgens de formule der valbeweging mocht het maar 4 sec zijn: het verschil is natuurlijk te wijten aan de luchtweerstand. Eigenlijk is het verrassend dat het water nog zo snel aankomt. Want men kan door proeven laten zien dat een vallende watermassa zich in druppels verdeelt die niet sneller kunnen vallen dan met een snelheid van 8 m/sec, hetgeen in dit geval een valtijd van 10 sekunden zou opleveren; werd de snelheid groter, dan zou de sterkere luchtstroom de druppels fijner verdelen, en zo zou de luchtweerstand hen weer sterker remmen. - Hier is blijkbaar de afstand van 80 m nog te klein, het water wordt niet ineens tot druppels uiteengeblazen. Men zou moeten beproeven hoelang druppels water er over doen. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
153. Stand van vallende voorwerpen.Tot 1906 heeft men aangenomen dat vallende voorwerpen zich zó instellen dat hun weerstand een minimum is. Toch zijn de eenvoudigste waarnemingen al voldoende om te laten zien dat het meestal andersom is! Bladeren, veren, een stuk papier stellen zich min of meer horizontaal in, dus in de richting van grootste weerstand. Daarnaast kan men merkwaardige schom- | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 252]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
melende bewegingen waarnemen van het blad, een draaiende beweging van het reepje papier (fig. 121). Men kan de instellingsrichting van verschillende meetkundige lichamen goed bestuderen door ze in een rauwe aardappel of in ebbenhout uit te snijden en ze dan in een emmer water te laten vallenGa naar voetnoot1); de draaiingen en schommelingen zijn dan veel minder storend. Beproef het met een plaatje en met een staafje. Aan een Fig. 121. Beweging van vallende voorwerpen. Links: zigzaglijn beschreven door een vallend blad papier. Rechts: snelle draaibeweging van een smal reepje papier.
uitgehold plaatje kan men goed zien dat de voorwerpen toch niet altijd de stand van grootste weerstand uitkiezen; want dit draait zich met de bolle zijde naar beneden, terwijl de weerstand groter zou zijn met de bolle zijde naar boven § 80. Ook sneeuwvlokken hebben ongeveer die vorm, en keren de bolle zijde naar beneden. Deze waarnemingen en proeven zijn o.a. van belang voor de verklaring der optische verschijnselen die door ijskristalletjes in de dampkring veroorzaakt worden (I § 141-143). Plaatjes en naaldjes zullen hoofdzakelijk horizontaal vallen, als de lucht maar zeer rustig is. Ook tafelvormige combinaties van zuiltjes en plaatjes komen onder de ijskristalletjes voor; met onze aardappelmodelletjes vinden we dat het tafeltje waterpas, het daaraan vastzittend zuiltje loodrecht gaat staan, maar wat van de twee boven en wat onder komt hangt af van de verhouding der afmetingen. Men zou zo gaarne aan de ijskristalletjes zelf waarnemen hoe ze zich bij hun zweefvlucht richten. Bij grote koude kan men soms de afzonderlijke plaatjes en sterretjes zien vallen, en neemt dan waar dat ze zich in zeer rustige lucht werkelijk waterpas instellen, terwijl ze bij wat meer luchtbeweging alle standen innemen.Ga naar voetnoot2) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
154. De windrichting.Westenwind is wind uit het Westen. Van waar komt de wind vandaag? - De vraag lijkt eenvoudig, maar is het niet! Want de windrichting bij de begane grond is anders dan boven de daken | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 253]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
der huizen, en weer anders in de verschillende wolkenlagen.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 254]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
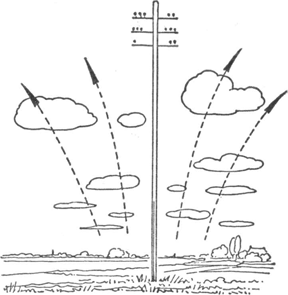
Vergelijk dikwijls de windrichting hier beneden en de richting der wolken. Vooral in de nabijheid van lage druk-gebieden vindt u de afwijkingen altijd in dezelfde richting: de waarnemer die naar de richting kijkt vanwaar de wind komt, ziet de wolken van rechts op zich aankomen; hoe hoger
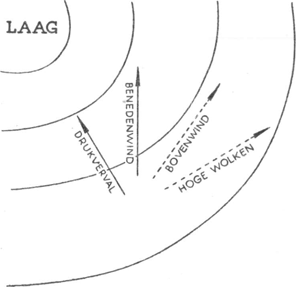 Fig. 123. De windrichting in de nabijheid van een lage druk-gebied, volgens de wet van Buys Ballot.
de wolken, hoe sterker 't verschil (fig. 123). Verklaring: in het algemeen waait de wind niet van de gebieden van hoge druk naar de gebieden van lage druk, maar hij wijkt af naar zijn rechterzijde: ‘wet van Buys Ballot’. Oorzaak: de aswenteling der Aarde en de daaruit volgende versnelling van Coriolis. Hoe geringer de wrijving, hoe sterker die afwijking naar rechts wordt; ze is dus in hoge lagen van de dampkring nog uitgesprokener dan hier beneden. Hieruit volgt de hoger opgegeven regel. Op zee is de windrichting te bepalen uit de richting waarin het schuim van de golven weggeblazen wordt of waarin de zeeën voortbewegen. Zeer dikwijls is dit een geheel andere richting dan die waaruit de deining loopt, opgelet dus! Vgl. § 93. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
155. De windsnelheid.‘Snel als de wind ....’ Hoe snel is dat eigenlijk? - Helemaal niet bijzonder snel! Let op dorre bladeren die door een windstoot meegenomen worden; natuurlijk bewegen ze iets trager dan de wind zelf, maar daar ze achtereenvolgens opwervelen overal waar de wind komt, is de ware windsnelheid licht te schatten: enkele meters per sekunde. Of nog eenvoudiger: zoek een rechte weg die ongeveer in de richting van de wind loopt, en fiets nu met de wind mee. Als u langzaam fietst voelt u de wind van achter komen, als u snel fietst, van voren; bij een gemiddelde snelheid voelt u nu eens een zwakke windstoot in uw gezicht, dan tegen uw rug. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 255]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Bepaal nu uw snelheid: het is de snelheid van de wind. U heeft daarenboven zeer duidelijk gemerkt dat de wind altijd onregelmatig waait, en dat we alleen een gemiddelde snelheid kunnen aangeven. - De getallen die u aldus vindt zijn verrassend gering. De vraag is echter of de windsnelheid niet aanzienlijker zou zijn op grotere hoogte. Om te beginnen kunnen we de snelheid schatten van de rook die uit een fabriekschoorsteen komt. U weet dat u een hoek van ongeveer 20o kunt bepalen door de arm zover mogelijk uit te spreiden: de bedoelde hoek komt overeen met de afstand van top duim tot top pink (§ 2b). Stel u nu op een paar honderd meter van de fabrieksschoorsteen, en zo dat u hem ziet in een richting, nauwkeurig loodrecht op die van de heersende wind. U kunt dan vrij goed een of andere kenmerkende kronkel van de opstijgende rookzuil in het oog vatten, en opmerken hoeveel sekunden die kronkel nodig heeft om zich over 20o te verplaatsen. Stel t; de hoeksnelheid is dus 0,35/t radialen; en als A de afstand is van Uw oog tot aan de schoorsteen, is de lineaire snelheid van de rook 0,35A/t. We kunnen echter ook de snelheid van de wind op wolkenhoogte bepalen! - Op een dag dat er mooie, afzonderlijke wolken zijn in blauwe lucht, kunnen we de wolkenschaduwen prachtig zien lopen over het wijde land. Het mooist gaat dit in uitgestrekte zandstuivingen of weilanden, waar men soms hele wolkenlandschappen in de schaduwen terugvindt; maar ook midden in de stad, in een straat die evenwijdig aan de windrichting is, hebben we gelegenheid de wolkenschaduwen te volgen. Let op hoeveel sekunden ze nodig hebben om een gegeven afstand te doorlopen, bepaal die, bereken de snelheid per sekunde. Omdat de zon zo héél ver weg is, kunnen we rustig zeggen dat de snelheid der wolkenschaduwen praktisch gelijk is aan die der wolken zelf. - We vinden dat de snelheid van de wolken altijd veel groter is dan die van de wind hier beneden. Oorzaak: de wrijving van de wind tegen de aarde. Op zee is die wrijving gering en de wind dus sterk. In bossen is de wrijving groot en de lucht windstil.Ga naar voetnoot1) Als u in de trein bent, op een recht stuk van de baan dat ongeveer evenwijdig aan de windrichting is, moet u eens een blikrichting scherp bepalen door langs twee staven van de coupé | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 256]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
te mikken, of langs een staaf en een vensterkruis. Verplaatst die viseerlijn zich ten opzichte van de wolken? Meestal haalt ze hen in; hun snelheid is dus kleiner dan de 25 m/sec die de trein ongeveer aflegt. Let op hoe het tafereel verandert zodra de trein stopt! 't Is helderblauwe locht, geweerd de wolkendriften, die, varend voor den wind, uit onzen hemel schijften; terwijl, benedenwaart, op huis en vore en veld, hun duister schaduwbeeld, onvatbaar, henensnelt. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
156. Een schaal voor de windsnelheid.Sedert vele jaren hebben de zeelui en de meteorologen zich geoefend in het schatten van windsnelheden zonder enig instrument, eenvoudig uit de uitwerkingen van de wind die we om ons heen waarnemen. De Engelse admiraal Beaufort, in 1805, bepaalde de graden van de naar hem genoemde schaal volgens de snelheid en de takelage van een fregatschip bij verschillende windsterkten. Men gebruikt de ‘schaal van Beaufort’ in die betekenis niet meer; de graden zijn nu als volgt bepaald.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 257]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Deze windsnelheid geldt voor een hoogte van 6 meter, dichter bij het aardoppervlak is ze op hetzelfde ogenblik veel kleiner. Het toenemen met de hoogte h is ongeveer te beschrijven door een wet van de vorm v = v1h0.30, waarbij v1 de snelheid op 1 m hoogte voorstelt; op 6 m hoogte is de wind tweemaal sneller dan op 1 m, op 30 m driemaal sneller. Deze wet hangt natuurlijk samen met de wrijving, dus met de begroeiing en de oneffenheden van het terrein. In hogere lagen neemt de exponent van h geleidelijk af tot 0,06. - Dikwijls kan men waarnemen, hoe een vogel betrekkelijk moeilijk opvliegt, tot hij een hoogte van enige meters bereikt heeft, en dan plotseling steil opstijgt in de sterkere wind die op die hoogte waait. Om de betekenis der graden van de Beaufortschaal te onthouden, kunnen we 't formuletje gebruiken: snelheid in 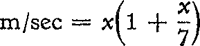 ; x is de graad van de Beaufortschaal. Nog eenvoudiger is te onthouden, dat de opeenvolgende graden ongeveer overeenkomen met de reeks der oneven getallen.
De windsterkte aan boord van een zeeschip moet afgeleid worden uit de wisselende vormen van het zee-oppervlak zelf; verschijnselen aan boord van het schip zijn minder bruikbaar, daar de snelheid van het schip zich dan samenstelt met die van de wind. Door lange oefening heeft de zeeman een grote zekerheid verkregen in het schatten van de ware windsterkte. De volgende tabel geeft enigszins weer waarop men te letten heeft (schaal van Petersen); de graden en de snelheden komen overeen met de schaal die voor het land geldt.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 258]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Op een zelfde ogenblik is de windsnelheid dicht boven een groot wateroppervlak ruim de helft groter dan over het land, een gevolg van de geringere wrijving -. Ook hier neemt de wind in de eerste meters snel met de hoogte toe; bijvoorbeeld:
Denk niet, dat de graden der windsterkteschaal geheel en al gekenmerkt worden door de windsnelheid in m/sec. Bij iedere graad behoort een eigenaardige toestand van de lucht en van het landschap, die zo goed mogelijk is uitgedrukt in de sobere beschrijving. Verder bemerke men, dat deze schaal feitelijk niet alleen de snelheid van de wind meet, maar wellicht nog meer zijn onbestendigheid; deze neemt gemiddeld met de windsterkte toe. Bij een gegeven gemiddelde snelheid v variëert de feitelijke snelheid meestal tussen 0,2 v en 2v. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 259]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
157. Verwoestingen door orkanenen aangericht.De schade, bij storm aangericht, kan een denkbeeld geven van de grootste windsterkte die geheerst heeft. Een felle wind van snelheid v m/sec oefent ongeveer een druk uit van 0,08 v2 kg/m2. Een muur waarvan de hoogte h is en de dikte d, wordt omvergeblazen bij een windsnelheid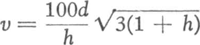 (alles in meters en meters per sekunde). Het zijn vooral de vlagen en windstoten die schade teweegbrengen. Merkwaardig is het, hoe na een orkaan soms in een heel woud slechts enkele sparren ontworteld zijn. Waarom juist die en niet andere? De wind waait met onregelmatige stoten, maar iedere boomstam heeft zijn eigen trillingstijd (§ 59), en al die stammen trillen dus in zeer verschillende mate met de wind mee. Die welke toevallig een trillingstijd hebben welke overeenkomt met de gemiddelde periode der windstoten, zullen het sterkst meetrillen en het eerst omvallen. Daarenboven is gebleken dat de grootste windsnelheden slechts over gebieden van enkele tientallen meters voorkomen. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
158. Windsterkte en richting aan boord van een schip.De windsterkte die men aan dek voelt is van punt tot punt verschillend. De beste indruk van de gemiddelde windsterkte krijgt men direkt achter de boeg; elders is de snelheid meestal te klein, op de brug is ze te groot. Men kan die snelheid schatten volgens de drukking die we van de wind voelen, of die met een anemometer bepalen. Dit is echter slechts de schijnbare snelheid S, resultante van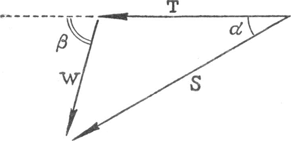 Fig. 124.
de ware wind W en de ‘tegenwind’ T van het bewegende schip (§ 19). Nu volgen enkele manieren om de ware wind te vinden.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 260]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
159. Het meten der windsnelheid met de katathermometer.Ik heb lang gezocht naar een eenvoudig toestel, dat zou toelaten de windsnelheid objektief te meten. Telkens bleek, dat de onophoudelijke snelheidsveranderingen en de wisselvalligheid van de luchtbeweging een onoverkomelijke hinderpaal vormden. Het is duidelijk dat we een instrument moeten hebben dat over een niet te korte tijd optelt en dat aldus de gemiddelde windsnelheid levert, zoals de windmeter van Robinson dat voor de vakmeteorologen doet. De katathermometer bleek mij tenslotte de gewenste oplossing te geven.Ga naar voetnoot1) We gebruiken een gewone alkoholthermometer met groot reservoir, die we tot 50o C verwarmen, en in de wind laten afkoelen tot het verschil met de luchttemperatuur op ⅔ van het aanvankelijke teruggebracht is. De tijd, nodig voor het afkoelen, is een goede maat voor de windsnelheid. Het verwarmen geschiedt gemakkelijk met heet water in een thermosfles; zodra de thermometer 65o C bereikt heeft, drogen we hem snel af en houden hem op het punt waar we de windsnelheid willen bepalen, terwijl we onmiddellijk sekunden beginnen te tellen op het ogenblik dat de dalende kwikzuil het getal 50 passeert. Stel dat de luchttemperatuur t is, dan wachten we dus volgens onze afspraak tot de thermometer de temperatuur x bereikt heeft, gegeven door: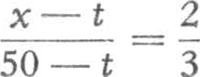 , ofwel 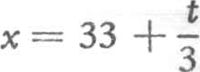 . | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 261]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
De bepaling van de afkoelingstijd T kan nog gemakkelijker geschieden met de thans zo goedkope stophorloges. We moeten onze windmeter eens en vooral ijken. Dit geschiedt voor windsnelheden tot 5 m/sec door op de fiets te springen, de thermometer voor u uit houdend, en met bekende snelheid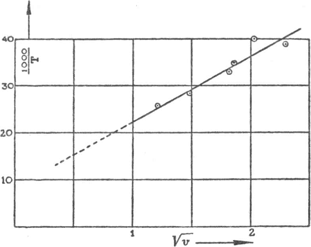 Fig. 125. Het meten der windsnelheid met de katathermometer: verband tussen de afkoelingstijd T en de windsnelheid v. (Deze lijn is voor elke thermometer verschillend).
te rijden. Voor grotere snelheden neemt u hem op een auto mede, zorg dragend hem ver zijdelings uit te steken. Maak een grafische voorstelling van 1000/T tegen √v. U vindt een lijn die bij benadering recht is, en die nu verder kan dienen om uit elke bepaling van de afkoelingssnelheid de onbekende v af te lezen (fig. 125). Bepaal aldus de windsnelheid op verschillende hoogten (groot verschil tussen 0 en 2 m; verder hoge ladder, uitzichtstoren, kerktoren). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
160. Het oplaten van een loodsballonnetje.Met een ballonnetje zoals dat wat we gebruikt hebben voor de studie van de luchtweerstand, kunnen we de hogere luchtlagen verkennen, aldus op eenvoudige wijze nabootsend wat de meteorologen dagelijks met veel volmaaktere instrumenten uitvoeren. We bepalen zijn stijgkracht; ook meten we zijn omtrek, en berekenen daaruit het oppervlak zijner doorsnede (§ 148). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 262]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Als we nu ons ballonnetje loslaten, zal het stijgen met een snelheid die we uit onze vorige proeven reeds kennen (zie de formule blz. 208!). Tevens neemt de wind het mee in horizontale richting, maar zonder een merkbare invloed te hebben op zijn vertikale stijgkracht v; de twee bewegingen gebeuren dus onafhankelijk van elkaar. Als we na een tijd t het ballonnetje in een richting zien die een hoek ϑ met de horizon maakt, kunnen we dus berekenen op welke hoogte h = vt het zich bevond, en op welke horizontale afstand h cot ϑ het van ons verwijderd is. Om het ballonnetje te kunnen volgen, bevestigen we met 4 flinke spijkers een toneelkijker op een plankje, zo dat de as van de kijker nauwkeurig evenwijdig aan de rand van het plankje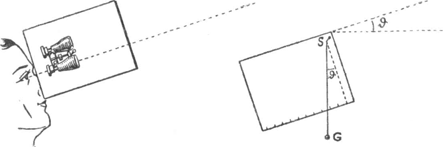 Fig. 126. Het volgen van een loodsballonnetje.
gericht is (fig. 126). Aan de achterkant hangt een draadje aan een spijker S, bezwaard met een gewichtje G en als schietlood dienend. De stand van het plankje t.o.v. dit schietlood is af te lezen aan een cm-schaal onderaan, en daaruit is de hoek boven de horizon onmiddellijk te vinden (vgl. § 2, i). Als de toneelkijker op de gezichteinder gericht is, moet het schietlood bij schaaldeel 0 hangen. - Wie geen toneelkijker heeft, gebruikt het plankje zelf en viseert langs de rand. Als we nu nog een horloge met sekundenwijzer bij de hand hebben, is al het nodige voor onze proef klaar. We begeven ons op een punt met vrij uitzicht aan de kant naar waar de wind waait, vergezeld van een kameraad die de aflezingen zal doen en alles zal optekenen. Opgelet! Nu! - Het ballonnetje wordt precies bij 't begin van een minuut losgelaten, de een volgt het in de kijker, de ander leest telkens na een halve of hele minuut de stand van het schietlood af, en schrijft op. O, wat is dat bolletje gauw kleiner en kleiner geworden, nu slechts een kleine donkere stip tegen de lucht! Verlies het niet uit het gezicht, of u vindt het | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 263]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
niet meer terug! Ineens verdwijnt het op een gegeven ogenblik in een wolkenlaag; of als er geen wolken zijn wordt het zo klein dat we 't niet meer volgen kunnen. We kunnen nog een tweede proef nemen met een dergelijk ballonnetje waaruit we eerst wat gas hebben laten ontsnappen door het buisje onder aan de ballon voorzichtig even open te maken. Zeer treffend in ons geval (en bijna altijd) is, dat de hoogtehoek voortdurend afneemt gedurende elke proef; dat bewijst natuurlijk dat de windsnelheid groter wordt naarmate men hoger komt. Verder kunnen we onmiddellijk de hoogte van de wolkenlaag vinden. U merkt ook op, dat de tweede proef langzamer verloopt dan de eerste; het duurt veel langer eer het ballonnetje de wolkenlaag bereikt, en in die tijd is het verder door de wind meegevoerd, wat uit de geringere hoogtehoeken blijkt. Tenslotte berekenen we de gehele baan, door onze gegevens stelselmatig te bewerken op de wijze die men uit het volgende, aan de werkelijkheid ontleende voorbeeld kan zien. In dit geval steeg het ballonnetje, naar wij volgens blz. 208 berekenen, met een snelheid van 1,55 m per sekunde of van 93 m per minuut.
We kunnen de baan in een vertikaal vlak tekenen (fig. 127); bij de tamelijk geringe hoogten waarover we het ballonnetje kunnen volgen, is het meestal niet nodig rekening te houden met veranderingen in azimuthGa naar voetnoot1). Als alles goed is uitgevoerd, | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 264]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
stemmen de resultaten van onze twee proeven heel netjes overeen, mits de abscissenas voor het tweede figuurtje in de verhouding der stijgsnelheden veranderd wordt. Let op het toenemen der windsnelheid met de hoogte!
Herhaal de proef op een mooie dag 's ochtends en 's avonds. 's Ochtends is het toenemen der snelheid met de hoogte veelal uitgesprokener, 's namiddags geringer. Dergelijke ballonnetjes kunnen voorzien worden van een briefkaart met verzoek tot terugzending. In een bepaald geval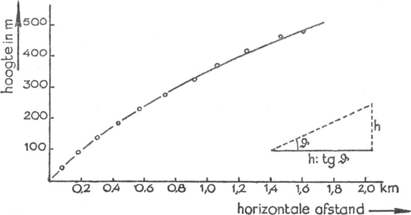 Fig. 127. De baan van een loodsballonnetje, met eenvoudige middelen bepaald.
was een eenvoudig kinderballonnetje in Zuid-Frankrijk terecht gekomen, na 430 km te hebben afgelegd. Een andere maal werd een dergelijk ballonnetje uit England in Zuid-Afrika teruggevonden! Meestal blijven ze slechts een half uur of een uur zwevende; hun snelheid is van de orde 60 tot 100 km/uur. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
161. De invloed van de plantengroei op de wind.Ga naar voetnoot2)In een dennebos neemt de wind niet op de normale manier met de hoogte toe; hij is vrijwel even zwak op elke hoogte (bv. 1 m/sec), tot wij boven de boomkruinen uitkomen, waar de windsnelheid snel toeneemt (fig. 128). Blijkbaar zijn er hier twee grensoppervlakken die een rol spelen, de grond en de boomkruinen. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 265]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Schat de sterkte van de wind in Beaufortschaal vlak achter
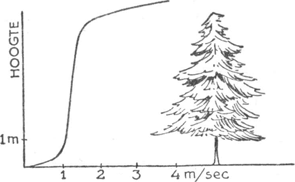 Fig. 128. De windsnelheid op verschillende hoogte in een dennebos.
een bos, in de ‘windschaduw’; dan 25 m verder; 50 m achter het bos is de windsterkte nog wel één graad zwakker dan in 't vrije veld; op 100 m is de invloed nog te merken, op 500 m is hij verdwenen. De invloed van een groep bomen is nog merkbaar op 6 tot 8 maal hun hoogte. Onderzoek bij stormwind de luchtstromingen in een open plek van het bos; dorre bladeren zijn voldoende om de bewegingsrichting na te gaan. Men vindt dat er zich een echte wervel gevormd heeft (fig. 129). - In een brandstrook waait de wind praktisch altijd in de richting van die strook, het sterkst is hij  Fig. 129. Windwervel in een open plek van het bos.
aan de rand naar dewelke de buitenwind waait. Staat de buitenwind toevallig precies loodrecht op de brandstrook, dan voelt men onregelmatige windstoten evenwijdig aan de strook, maar in beide richtingen.Ga naar voetnoot1) Leg u in de stormwind tussen de hoge heidestruiken en druk u goed tegen de grond: u voelt bijna geen wind. Door metingen vond men in een bepaald geval voor de windsterkte in de heide: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 266]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Binnen een afstand van een paar meter heerst dus een enorm klimaatverschil! We stellen ons niet voldoende voor, hoe anders het klimaat is voor een grashalmpje, voor een kevertje, dan voor de mens. De studie van het ‘mikroklimaat’ is van het grootste belang voor landbouw en biologie. Op Texel heeft men de weiden van elkaar gescheiden door lage dijkjes; deze geringe verhevenheidjes zijn voldoende om de snelheid van de wind die over de grond strijkt tot ⅓ terug te brengen van wat ze in een open vlakte is. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
162. Dorre bladeren.De herfst is de tijd bij uitnemendheid om luchtstromingen te bestuderen; de droge bladeren die met miljoenen overal langs de wegen dwarrelen, zijn heel gevoelige windaanwijzers. Bij elke greppel, bij elke ook zelfs heel geringe inzinking van het terrein, - al is het maar een golving van een paar centimeter diepte! - hopen de dorre blaren zich op. Op zulke punten moet de wind dus merkbaar minder sterk zijn. Andere opeenhopingen ontstaan waar de luchtstroom plaatselijk opstijgt, zodat de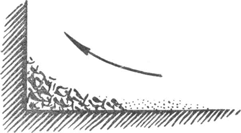 Fig. 130. Zand en dorre bladeren, door de wind opeengehoopt tegen een muur.
horizontale componente van de luchtbeweging klein wordt. Zo vindt men soms in de inspringende hoek van een gebouw een grote hoop bladeren, die ontstaat doordat de lucht daar dwarrelend opstijgt. En let maar eens op de zoom van bladeren die in de herfst langs elke stoep, langs elke muur te vinden is: naarmate de wind dichter bij de muur komt wordt zijn horizontale snelheidscomponente geringer, en zetten zich eerst het zand af, daarna pas de dorre bladeren (fig. 130). Soms vormen de dorre blaren voor een stoep zulk een grote hoop, dat telkens weer een der bovenste door de luchtstroom meegenomen wordt en op de stoep wipt. Aan de noordzijde van een plein kan men bij sterke zuidenwind de blaren over de hele | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 267]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
hoogte van een huis zien opstijgen, meegevoerd door de opstijgende stroom. Als een auto voorbijkomt, dwarrelen de dorre bladeren nog ongeveer 5 sekunden; in die tijd heeft hij misschien 80 meter afgelegd. Nu moeten we ons goed voorstellen dat de wervelingen en stromingen achter zulk een auto, die al lang zijn zelfde snelheid heeft, onveranderlijk met hem meelopen; er is dus een reusachtig groot wervelpatroon dat hem vergezelt en overal de lucht achter hem in roering brengt. Nog veel uitgebreider is dit achter een sneltrein, waarvan de wind nog na 9 sekunden de blaren doet dwarrelen: het wervelpatroon strekt zich hier dus over een lengte van wel 180 m achter de trein uit!
Een aantal bijzonderheden die we hier voor dorre blaren beschrijven zijn nog mooier waar te nemen aan de miljoenen fijne bruine schubbetjes die midden Mei de grond bedekken, overal waar er veel beukebomen staan; ze zijn afkomstig van de knoppen die pas zijn opengegaan. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
163. Stuwing van de wind om hoge gebouwen.Iedereen weet hoe hard het waaien kan nabij kerken en torens, vooral als die aan een open plein staan. Om die grote gebouwen te vermijden moeten de windbanen uitwijken, en zo worden zij in een kleine ruimte samengedrongen; dientengevolge moet de stromingssnelheid daar toenemen. Dikwijls vormen zich daarbij wervels (§ 120). - Te Groningen zegt men: ‘Als het tussen beide markten niet regent en bij de Aa-kerk niet waait, dan is het mooi weer.’ Prachtig ziet men aan het strand de stuwing van de lucht tegen de dijk en tegen de eerste duinenrij. De sterke opstijgende wind loopt in zilveren golven over de helm van de duinhelling. Meeuwen zweven uren lang in de opstijgende stroom, nauwelijks af en toe eens met de vleugels slaande. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
164. De wind in de schoorsteen.Ga naar voetnoot1)De wind die over de monding van een schoorsteen strijkt, zuigt de verbindingsgassen naar buiten door een aerodynamisch meeslepingseffekt (zoals bij de verstuiver van een kapper). Als de wind schuin naar beneden blaast, wordt de zuigkracht der | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 268]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
horizontale componente tegengewerkt door de benedenwaartse componente; men bewijst dat ze elkaar net opheffen als de
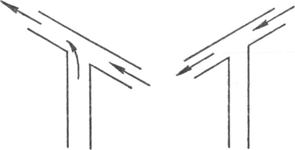 Fig. 131. Opzuigen van de rookgassen door de wind die over de schoorsteen strijkt. Links: maximale zuigkracht. Rechts: zuigkracht net opgeheven.
windstroom onder 30o naar beneden gericht is (fig. 131). De maximale zuigkracht ontstaat als de wind onder 30o naar boven blaast. Met een loodrecht T-stuk boven de schoorsteen is de zuigkracht praktisch alleen werkzaam en de kans op inslaan zeer gering. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
165. Invloed van de wind op het waterpeil.Franklin verteltGa naar voetnoot1), dat een vijver, 3 mijl lang en 0,90 m diep, door een stormwind aan de ene kant geheel en al drooggelegd werd, terwijl het water aan de andere zijde 1,80 m diep was geworden. Heeft u ooit iets dergelijks kunnen waarnemen? - In de jaren '90 is het voorgekomen, bij een aanhoudende felle storm, dat het Winschoterdiep vrijwel droogwaaide van de sluis te Zuidbroek tot aan de Kromme Rakken, over een afstand van ruim 2 km! Er bleef zo weinig water over, dat de jeugd naar allerlei voorwerpen in de modder aan 't zoeken was.Ga naar voetnoot2) - Met de nauwkeurige peilschalen van de Waterstaat heeft men gevonden dat het oppervlak der Noordzee schuin gaat staan door de wrijving die de wind op het zee-oppervlak uitoefent. - Toen de afsluitdijk nog niet gereed was, kon men te Durgerdam, aan het buiten-Y, waarnemen dat het water bij felle Noordenwind soms tot 2 m hoger dan normaal stond, terwijl het bij harde Westenwind evenveel zakte, zodat botters die buiten voor anker waren gegaan op het droge kwamen te liggen. In de Oranjesluizen werd dan niet meer geschut, omdat er zelfs in de vaargeul te weinig water stond.Ga naar voetnoot3) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 269]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
166. Vlieger.Ga naar voetnoot1)Verschillende modellen zijn hieronder getekend (fig. 132); houten latjes zijn door een dubbele lijn aangegeven, touwen door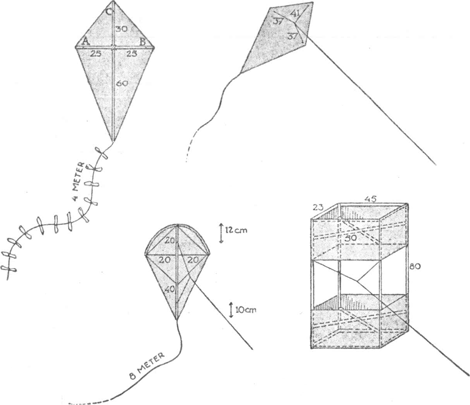 Fig. 132. Verschillende modellen van vliegers.
 Fig. 133. Hoe de winddruk een vlieger doet opstijgen.
een enkele, gearceerd is wat met papier of linnen bedekt wordt. De vlieger verheft zich in de lucht, als de winddruk er een schuin opwaarts gerichte componente op uitoefent; daartoe is de eis, dat de vlieger zich schuin ten opzichte van de wind instelt op de wijze van fig. 133. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 270]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Deze instelling wordt verkregen, hetzij door het aanbrengen van een staart, hetzij door te maken dat het ondereind van de vlieger zwaarder is dan het boveneind, dus door het aanbrengen van het touw boven het midden. Ten onrechte denken velen, dat het doek of papier van een vlieger strak gespannen moet zijn. Het tegendeel is waar! Een vlieger waarvan het draagvlak zo los is, dat het zich door de winddruk welven kan, stijgt hoger, en het touw is steiler opwaarts gericht. Bij een goede vlieger stelt het touw zich vrijwel vertikaal in! Zo groot is de dwarse stijgkracht die de wind ontwikkelt; terwijl hij helemaal geen neiging vertoont, de holle vleugel in zijn eigen bewegingsrichting te verplaatsen. Voor modelvliegtuigen verwijs ik naar: H. Hahn, Physikalische Freihandversuche, 2, 372 en vlg. (Berlin, 1916). - V.E.R. Alberts, Modelvliegtuigen Bouwen (Amsterdam, Ahrend, 1935). - W. van Pelt, Proefvliegtuigen (Amsterdam, Ahrend). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
167. Windmolens en windraderen.Ga naar voetnoot1)Waarom heeft een windmolen altijd 4 vleugels en nooit 8? Zou zijn vermogen dan niet verdubbelen? Zijn de moderne Amerikaanse windraderen met hun groot aantal vleugels niet doelmatiger gebouwd? De windmolen onttrekt energie aan de wind en gebruikt die voor het overwinnen van wrijvingen bij het malen. Dat onttrekken van energie komt daarop neer, dat de wind, die met een snelheid v1 tegen de wieken blaast, achter de wieken met een kleinere snelheid v2 wegstroomt. Als we de cirkel die door de wieken beschreven wordt met een toenemend aantal wieken vullen, en die wieken toenemend groot maken, zal aanvankelijk het vermogen van de molen stellig toenemen; maar weldra komt er een grens: er wordt wel veel snelheid aan de wind onttrokken, maar er wordt nu zó weinig lucht doorgelaten dat de molen bijna stil valt. - Waar is het optimum? Men bewijst gemakkelijkGa naar voetnoot1) dat de vulling door de vleugels zó moet zijn dat v2 = v1/3 (1) Want de arbeid die per sekunde aan de wind onttrokken wordt is ½mv12-½mv22, waarbij m de hoeveelheid lucht is die per sekunde doorstroomt; m is evenredig met de doorstroomsnelheid, waarvan men aantoont dat ze het gemiddelde is van v1 en v2. Het vermogen is dus evenredig met | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 271]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Nu neemt de remming r die de wieken op de wind uitoefenen niet alleen toe als hun oppervlak f meer en meer vult van het totale oppervlak F dat bij de beweging bestreken wordt, maar ook als hun lineaire snelheid u ten opzichte van de windsnelheid v toeneemt; en wel is ongeveer
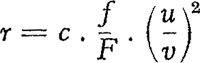 , waarin c een constante is. Willen we dus de wind voldoende remmen om te voldoen aan de voorwaarde (1), dan moet r een zeer bepaald bedrag hebben, en dan ziet men  . Hoe sneller de molen draait, hoe kleiner de vullingsgraad moet zijn. (2) Schat nu eens de (lineaire) snelheid der wieken van een ouderwetse windmolen en van een Amerikaans windrad! Natuurlijk is die snelheid klein voor punten dicht bij de as, maar ze neemt toe voor punten die verder van de as verwijderd zijn; de vullingsgraad neemt tegelijk daarmee naar buiten af. Om de gedachten te bepalen beschouwen we een punt van de omtrek. We vinden nu bv. voor een windmolen: 10 m/sec en voor een windrad 4 m/sec; de vullingsgraden moeten zich nu verhouden als (4/10)2 of 16/100. Het is dus volmaakt begrijpelijk dat de windmolen veel minder vleugels heeft dan het windrad! Schat empirisch de waarde der constante in formule (2), zowel voor het windrad als voor de windmolen, uitgaande van de gemiddelde windsterkte waarbij de molen gebruikt wordt. Wat is het vermogen dat een molen kan leveren? Door het bestreken oppervlak F stroomt per sekunde een hoeveelheid lucht vF, die γ kg per m3 weegt en een arbeidsvermogen van beweging 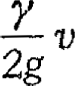 heeft. De molen kan dus in beginsel per sekunde beschikken over 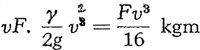 . Door verschillende omstandigheden levert hij echter van dit bedrag slechts het kleine gedeelte Ce Fv3/16 kgm per sec.
Met modellen in de windtunnel, waar een gelijkmatige windstroming heerst, bereikt men ongeveer Ce = 0,3. Bij werkelijke molens blijft men lager, tengevolge van de ongelijkmatigheid van de wind. De Prinsenmolen te Hillegersberg gaf met de oude wieken Ce = 0,09; nadat het wiekprofiel was verbeterd, door de voorkant van elke wiek (de ‘roede’) te bekleden met een | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 272]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
mooi afgeronde metalen mantel, was de weerstand bij het doorklieven der lucht aanzienlijk geringer geworden, zodat Ce = 0,17 werd bereikt. Een belangrijk bezwaar is steeds de remming van de wind door de molenromp. Bereken in paardekrachten het vermogen van een windmolen, van een windrad, van een tuinmolentje; 75 kgm per sekunde = 1 paardekracht. De snelheid aan de omtrek is als kenmerk gekozen voor de volgende indeling:
Schat de windsterkte op de plaats van de molen (volgens §§ 156, 159) en bepaal telkens de daarbij passende omtreksnelheid; doe dit bij verschillend sterke wind en neem telkens de verhouding u/v. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
168. Laminaire luchtbeweging langs gestroomlijnde oppervlakken.Het is een echt Hollands gezicht, als de hagelwitte was aan de waslijn hangt te fladderen, helder in de zon tegen een achtergrond van groene weiden en blauwe lucht! Aan die fladderende dingen valt er echter ook een natuurkundige waarneming te doen: strak aangespannen stukken klapperen onregelmatig op en neer; ruim aangespannen stukken daarentegen gaan bol staan in sierlijke welving, zij waaien constant uit, niet alleen tot in de horizontale stand, maar zelfs nog hoger, in schuin opwaartse richting. In het eerste geval vormt de wind aan de randen van het doek overal wervels, die een voor een loslaten en daarbij echte stoten veroorzaken: de stroming is turbulent. In het tweede geval neemt het oppervlak de stroomlijnvorm aan, de luchtdeeltjes kunnen nu zonder werveling, laminair voorbijglijden. En nu zien we ook hoe een horizontale wind, langs een dergelijk zacht opwaarts gewelfd oppervlak strijkend, er een opwaartse druk op uitoefent. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 273]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
We herinneren ons hoe een vlieger beter opstijgt als het doek los gespannen is en hol gaat staan (§ 166); hoe de zeiler opzettelijk voor welving van zijn zeilen zorgt, teneinde de windkracht beter te gebruiken (§ 65). - We letten ook op de doorbuiging van de vogelvleugel, die zo volmaakt aan de beweging door de lucht is aangepast. - Die merkwaardige dwarse kracht, door een windstroom op een gebogen oppervlak uitgeoefend, wordt voortdurend in de vliegtechniek gebruikt; het vleugelprofiel wordt nauwkeurig zo gevormd dat de stijgkracht zo groot mogelijk is (‘oppervlak van Joekovski’). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
169. Laminaire en turbulente stroming in een lucifersdoosje.Ga naar voetnoot1) (fig. 134).Een echt roker houdt er zijn eigen methode op na, om bij winderig weer een lucifer aan te steken en aan 't branden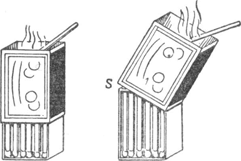 Fig. 134. Turbulente en laminaire luchtstroming in een lucifersdoosje.
te houden. Natuurlijk kunt u met de rug naar de wind gaan staan; maar dat is dikwijls onvoldoende. Beter helpt het, wanneer u het lucifersdoosje voor ¾ uit de huls schuift, en de lucifer onmiddellijk na het aanstrijken in de beschermende holte van de huls brengt. - Maar daar hoort nog een kunstgreep bij! Merk op hoe onregelmatig devlam brandt, hoe ze flakkert en rechts en links weggeblazen wordt: klaarblijkelijk zijn er werveltjes, die dikwijls de lucifer uitdoven. Dit vermijdt u, door de huls zóver uit te schuiven, dat het doosje er schuin in kan, en dat u bij S een spleet kunt open houden. De lucifer brandt nu veel regelmatiger en dooft niet uit; als de wind te sterk wordt, kunt u de spleet nauwer maken, als hij luwt, weer wijder. Denk niet dat de rol van de spleet daarin bestaat dat er meer verse lucht door aangevoerd wordt voor de verbranding: als u de proef zonder spleet in een rustige kamer neemt, flakkert de vlam niet, ze heeft dus zuurstof genoeg. Het verschil is echter te zoeken in de stromingswijze van de lucht, die met spleet laminair is, zonder spleet turbulent. Het zijn de twee kenmerkende bewegingsvormen die we ook bij stromende vloeistoffen al hebben leren kennen (vgl. § 78, 168). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 274]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
170. Draaiende regendruppels. (fig. 135)Ga naar voetnoot1)Van de grote regendruppels op de treinruiten, die aan het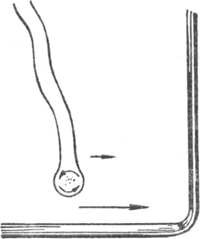 Fig. 135. Draaiende regendruppel op de ruit van een trein.
eind van hun baan gekomen zijn, bevinden er zich een aantal in draaiende beweging; kleine stofjes en roetkorreltjes van de rook der lokomotief, die er in zijn komen waaien, worden door die beweging meegevoerd en wijzen ze aan. Het gaat vrij snel: wel een paar omwentelingen per sekunde, en altijd in dezelfde zin: blijkbaar is de windstroom 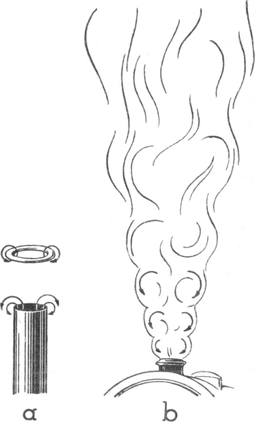 Fig. 136. Wervelingen boven de uitlaatpijp a) van een benzinemotor, b) van een lokomotief.
aan de onderkant van de druppel sneller dan aan de bovenkant. Aan het raampje aan de andere zijde van onze coupé geldt dezelfde regel. We moeten dus aannemen, dat de luchtstroom aan de bovenkant van de druppel geremd wordt door de sporen van de druppelbaan die zich nog op de ruit bevinden; het verschil in snelheid van de windstroom onder en boven de druppel geeft aanleiding tot de draaibeweging. Als de trein stopt houdt de werveling op; zet hij zich weer in beweging, dan begint het wervelen met stootjes, onregelmatig, tot zich langzamerhand een stabiele toestand heeft ingesteld. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 275]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
171. Wervelringen.De schepen die op onze binnenwateren varen hebben thans haast alle een petroleum- of benzinemotor. Uit het schoorsteenpijpje, waaruit de verbrandingsgassen puffen, komen dikwijls prachtige wervelringen van rook, die bij elke zuigerslag de lucht in geschoten worden (fig. 136). Zij ontstaan doordat de rookgassen nabij de wand van de buis wrijving ondergaan; in de meer centrale delen is dus de snelheid groter, en bij het uitstromen gaan die om de randlagen draaien. De aldus gevormde wervelring schiet recht en snel als een projektiel naar omhoog, het is iets geheel anders dan de gewone dwarrelende rookpluim die zich langzaam, aarzelend verheft. Kelvin en Helmholtz hebben laten zien dat in een ideale (wrijvingsloze) vloeistof zulk een wervelring, eenmaal gevormd, nooit meer verdwijnen kan; en zij dachten hier een beeld te zien van de oerbouwsteen der materie: een ‘atoom’, dat bestaan zou uit een wervelring in de aether. Herhaaldelijk kan men opmerken hoe een wervelring A, die toevallig wat krachtiger is afgeschoten, de vorige B inhaalt; dan trekken ze elkaar aan, en bliksemsnel kruipt A door B! Ik heb zelfs eens gezien hoe B, die nu de onderste geworden is, op zijn beurt weer door A kroop! - Het gaat echter alles heel snel. De stoom die uit de schoorsteen van een lokomotief opstijgt vormt ook wervelringen, maar veel minder duidelijk; toch ziet men de wervelende beweging nog wel in de eerste puffen van een vertrekkende trein (fig. 136b). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
172. Windwervels.Meer dan eens zien we hoe de wind gaat wervelen in de inspringende hoek van een gebouw; stof en dorre bladeren dwarrelen Fig. 137. Windwervels achter de duinen.
op, er zijn zelfs gevallen bekend dat het water van een vijvertje door zulk een wervel tot 8 meter hoogte werd meegevoerd en opgezogenGa naar voetnoot1)! Minder heftig, maar groter van afmetingen zijn de wervels die zich achter elke heuvel ontwikkelen in golvend landschap: als men in de luwte de helling beklimt, voelt men dikwijls de wind | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 276]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
in de rug (fig. 137). Geregeld kan men dit opmerken wanneer men bij Westenwind tot onze duinen nadert van de landzijde. In de meeste duinpannen kan men duidelijk voelen dat er zich een wervel heeft gevormd. De grote koepel van het Kurhaus te Scheveningen is omringd door vier kleinere koepels, elk met een vlag. Als een der kleine koepels in de windschaduw ligt van de grote, ziet men zijn vlag in tegengestelde richting wijzen van de drie andere! Het is welbekend, dat de regenmeters op het platte dak van een gebouw, naast het gebouw en op grote afstand er vandaan een zeer verschillende hoeveelheid regen kunnen aanwijzen. Om het gebouw en om de regenmeters zelf ontstaan namelijk windstuwingen en wervels, die de regen ongelijk verdelen (II, § 140). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
173. Nevelzuilen.In de herfst en in het voorjaar, als 's nachts de lucht door straling is afgekoeld en 's ochtends het water warmer is dan de lucht die erover strijkt, vormen er zich riviernevels (vgl. II, § 99). Ook op zee is het verschijnsel bekend als het ‘dampen van de zee’. Men ziet dan soms hoe werveltjes in de nevellaag ontstaan, en hoe zich plaatselijk een draaiende beweging ontwikkelt. In een bepaald gevalGa naar voetnoot1) vormden zich honderden van die werveltjes in een half uur; ze hadden ongeveer 30 cm middellijn, waren tot 7 meter hoog, en bereikten een draaiingssnelheid van 1 omwenteling in 2 sekunden; elke wervel bleef maar een paar minuten bestaan. Boven de warme Golfstroom komen er in sommige jaargetijden nevelzuilen en hozen van allerlei afmetingen voor. Op het meer Ontario ziet men soms een nevellaag rusten, waaruit honderden nevelzuilen opstijgen, die zich in enkele sekunden tot een hoogte van 200 meter omhoogschroevenGa naar voetnoot2)! Nog een ander voorbeeld op kleine schaal werd waargenomen op een plein dat na een regenbui in de felle zonneschijn te blakeren lagGa naar voetnoot3); de granieten wandelweg om het plein was al opgedroogd, maar de aarde was nog nat en zwart; ze dampte. Reeds op kleine hoogte boven de grond condenseerde de damp. En nu zag men hoe zich miniatuurwervels vormden, van een 60-tal cm hoogte en een 60-tal cm middellijn, die langzaam draaiden, soms in de rechtse, soms in de tegengestelde zin. Het merkwaardige verschijnsel duurde wel een kwartier, tot de aarde weer droog was. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 277]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
174. Werveltjes boven 't verwarmde aardoppervlak.Boven het aardoppervlak dat door de zonnestralen verhit wordt heerst een steil temperatuurverval. De lucht die in aanraking is met de hete aarde is lichter dan de lucht in de omgeving en heeft neiging tot opstijgen, de toestand is dus labiel, precies als die van een kurk die zich onder in een glas water bevindt. Een uitgestrekte luchtmassa kan echter niet als een geheel opstijgen; maar als er hier en daar punten zijn waar het opstijgen begint, schiet de warme lucht als een fonteintje omhoog, en dan gaat de opstijgende luchtzuil meestal ook wervelen, doordat de lucht niet even sterk van alle kanten toestroomt. Men begrijpt dat de werveltjes zich dikwijls daar zullen vormen waar er een aanleiding tot opstijgen te vinden is: aan de rand van een plateau, boven een zandhoop, enz. De draaiingsrichting hangt van toevalligheden af, ze zal soms in de zin van het uurwerk zijn en soms tegengesteld. Op zulke sneldraaiende wervels heeft de draaiingsrichting der Aarde praktisch geen invloed, in tegenstelling met wat bij de grote gebieden van lage druk, de barometrische depressies, het geval is. Door de wijze van ontstaan en door de afmetingen onderscheiden de luchtwerveltjes die we hier bespreken zich trouwens scherp van de hozen en de grotere dampkringwervels. Klassieke voorbeelden van luchtwerveltjes heeft men waargenomen boven de hete lava der vulkanen en in de zandwoestijnen van Azië. Uit de volgende korte beschrijvingen zal men kunnen zien dat ze zich ook in onze gewesten vertonen en tot zeer merkwaardige verschijnselen aanleiding geven.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 278]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 279]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 280]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
175. Wind- en waterhozen.Ga naar voetnoot1) - (Plaat XIII.)Een hoos is werkelijk een zeer zeldzaam natuurverschijnsel; toch moet men bedenken dat er, alleen al in Noord-Nederland, gemiddeld een drietal per jaar worden waargenomenGa naar voetnoot2). Als men dus maar weet wat er op te merken valt en zijn ogen goed opendoet, heeft men nog een redelijke kans het grootse schouwspel te beleven. Op een warme zomernamiddag heeft de lucht zich verduisterd en is er een onweer opgekomen. Reusachtige cumulonimbuswolken rukken aan, het bliksemt en dondert, de wind is zwak en veranderlijk van richting. Daar begint de voorste donkere rand van een der cumulonimbuswolken benedenwaarts gerichte uitsteeksels te vertonen; ze verenigen zich tot een trechtervormig aanhangsel dat lager en lager daalt; als het dicht bij de grond komt, beginnen stof, bladeren, stro op te wervelen, tengevolge van de zuiging welke de hoos uitoefent. Om de voet vormt zich een echte wervelring, die er uit de verte uitziet als een soort ontzaglijke rookbal, en een paar honderd meter breed is. De zuil die daarboven opstijgt kan een 40 meter breed en een 1000 meter of meer hoog zijn; om haar heen stijgen het stof en de lichte voorwerpen op, zodat het duidelijk is dat de zichtbare wervel door een onzichtbare wervel omgeven is. De zuil zelf is hol, want op een heldere achtergrond gezien zijn de randen donkerder dan het midden; het is alsof er licht van boven in de centrale holte doordrong. Men ziet de dampen in een schroef- | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina t.o. 280]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 PLAAT XIIIa. Windhoos (§ 175).
Naar B.C. Elskamp, Hemel en Dampkring. 36, 353, 1938.  PLAAT XIIIb. Waterhoos (§ 175).
Naar C. van den Heuvel, Onweders enz., 57, 61, 1936. Clichés in bruikleen van het Ned. Meteorologisch Instituut. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina t.o. 281]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 PLAAT XIV.
Nalichtend spoor van een vuurbol (§ 181). Ongeveer 10 min. na het neerkomen gefotografeerd door den Heer A.J. van Stralen. (Vgl. Hemel en Dampkring 33, 171, 1935; Astrophys. Norvegica 3, 119, 1939). Cliché in bruikleen van het Ned. Meteorologisch Instituut. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 281]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
lijn omhoog of omlaag wervelen; in de meerderheid der gevallen (72%) is de draaiing tegengesteld aan het uurwerk (van boven gezien), dus zoals in de gebieden van lage barometerdruk. Voortdurend stroomt er van alle kanten lucht naar de hoos toe, maar tevens stroomt er aan de bovenkant evenveel lucht weg, zodat ze niet opgevuld wordt. Hoe meer wrijving, hoe smaller ze wordt; de trechtervormige vernauwing is dus een aanschouwelijk beeld van het toenemen der wrijving dichter bij de grond. In een aantal gevallen heeft men kunnen aantonen, dat de hoos niet ophoudt waar ze aan de wolk raakt, maar dat ze daar ombuigt en over verscheiden kilometers als horizontale wervel voortloopt. In andere gevallen vertoont de zuil boven een soort zak, die een aanwijzing zou kunnen zijn voor het bestaan van twee concentrische buizen: een korte buitenste en een lange binnenste buis. Ondertussen stort een hagelbui neer, terwijl de hoos zich van ons weg beweegt met een snelheid van 25 km/uur; het hoogste gedeelte gaat vooraan, de voet volgt en blijft iets achter, zodat de hoos in de windrichting helt; dikwijls voert ze slingerende slangenbewegingen uit. Waar ze over een woud trekt, worden de bomen bij honderden omvergeworpen, daken van huizen worden door de plotselinge zuiging als door een ontploffing omhoog gelicht, stenen uit de grond gerukt, allerlei zware voorwerpen soms kilometers ver vervoerd. De hoos maakt een gedruis als een wagen die over hobbelige straatkeien rolt, en sommige waarnemers beweren dat men in haar spoor een reuk van zwavel kan opmerken (ozon?). Als de hoos over een wateroppervlak strijkt, spreekt men van een waterhoos; het geluid wordt dan veel zwakker, het is veeleer een gesis. Aan de voet van de hoos ziet men een centrale uitholling in het wateroppervlak, waar omheen zich een kroon van dansende, puntige golven verheft. Er zijn zelfs gevallen waarin deze kroon zich hoger en hoger verheft en een echte watertoren vormt van 10 of 20 m hoogte of meer. Tracht waar te nemen of het water in het midden der hoos opgezogen wordt, ofwel of het slechts de voet van de zuil omringt. Een waterhoos is meer cylindrisch dan een windhoos, doordat de wrijving over 't water altijd veel kleiner is dan over land (zie hoger). Na een 10- of 20-tal minuten wordt het verschijnsel minder duidelijk; we bemerken uit de verte hoe het middengedeelte der zuil onzichtbaar wordt; het bovenste en onderste stuk trekken zich terug, worden breder, en langzamerhand verdwijnt de uitstulping van de wolken en bedaart het schuimende water. - Deze beschrijving dient alleen om u te laten zien wat er onge- | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 282]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
veer aan een hoos op te merken valt. Als u ooit zulk een verschijnsel waarneemt, zult u wel bevinden dat tal van bijzonderheden volstrekt niet precies kloppen: er zijn hozen die bij sterke wind ontstaan en niet bij windstilte; er zijn er die 3 uur duren en zich over 400 km verplaatsen; er zijn er die voorafgegaan worden door hagel (in plaats van erdoor gevolgd te worden). Soms vormen zich verscheiden hozen tegelijk of kort na elkaar; soms splitst sich een hoos in twee andere of ziet men er twee zich verenigen; men kent ‘blinde hozen’, waarvan de zuil niet zichtbaar is, maar waarvan de wervelbeweging te merken is aan de korte wolkentrechter en aan het water dat bij de voet opschuimt. - Men lette dus op al de hierboven genoemde bijzonderheden één voor één, en merke alle afwijkingen onbevooroordeeld op. Bepaal de hoogte en de breedte der zuil, alsook de hoogte en breedte van de voet in hun verhoudingen tot elkander; bepaal ook enkele dezer grootheden in hoekmaat: als u optekent hoe laat en waar die waarneming geschied is, en in welke richting de hoos gezien werd, kunt u later de afstand terugvinden, en de hoekmaten in ware lengten omzetten. In het algemeen worden de afmetingen door de waarnemers onderschat!
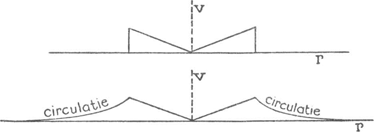 Fig. 138. De verdeling der windsnelheid in een jonge (boven) en in een oude hoos (onder). - Benaderd.
Als een hoos pas gevormd is, draait ze als een geheel, en in de wervel verschuiven de luchtdeeltjes niet ten opzichte van elkaar (fig. 138). Slechts na enige tijd begint de lucht om de wervel ook langzamerhand meegesleept te worden (‘circulatiegebied’), maar beweegt daar volgens heel andere wetten, waarvan fig. 138 een ruwe benadering geeft. Een nauwkeuriger theorieGa naar voetnoot1) leert, dat beide gebieden vloeiend in elkaar overgaan; op afstand r van het centrum en op een tijd t is de snelheid voor te stellen door de uitdrukking: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 283]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ging: de wervelende gassen zijn geen delen van de wolk, die al wervelend lager en lager afdalen, maar lucht die van alle kanten toestroomt, opstijgt, uitzet, en afkoelt; meestal condenseert daardoor de waterdamp, en wordt de hoos zichtbaar als een nevelige trechter. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
176. Het opnemen van de sporen van een hoos.Ga naar voetnoot1)Om een hoos te zien kunnen we niet veel anders dan .... een gunstig toeval afwachten! Maar wat iedereen kan doen: zodra een bericht in de kranten verschijnt, zich naar de plaats begeven waar de hoos heeft gewoed, nauwkeurig de sporen der verwoesting onderzoeken, de bewoners ondervragen (veldwachters, treinbeambten), hen de hoos naar hun herinnering laten tekenen, en alles in kaart brengen wat men te weten komt. Men kan op die wijze het gehele natuurverschijnsel als het ware weer voor zich opbouwen. 1. Eerst tekenen we op de kaart de weg die de hoos gevolgd heeft, en bepalen zijn lengte en breedte. Als hij knikken vertoont, hangen die dan samen met de ligging van dalen of rivieren, met de grenzen tussen bos en veld? De breedte blijkt volmaakt overeen te stemmen met de middellijn van de wervelring aan de voet van de hoos; ze is vele malen geringer dan de breedte van het hagelgebied dat bij de hoos behoort: een bewijs dat deze twee verschijnselen van geheel verschillende aard zijn. 2. Zeer belangwekkend is het optekenen van de omgevallen bomen, één voor één, met de richting waarin ze liggen; iedere boom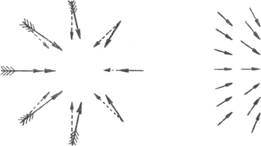 Fig. 139. Luchtstroming in een hoos. Links: radiaal toestromen (gestippelde pijlen) en de samenstelling van radiaal toestromen met de voortschrijdende beweging (voluitgetrokken pijlen); waar de windsterkte het grootst is zijn de pijlen gevederd getekend. Rechts: richting der omgewaaide boomstammen in het meest typische geval.
wordt door een streepje op millimeterpapier op de juiste schaal voorgesteld; de richting wordt met het kompas bepaald. Waar de hoos haar baan begon, liggen de boomstammen onregelmatig, maar verder bemerkt men weldra dat de weg van de hoos in drie stroken verdeeld is: in de middenste liggen de bomen in de richting waarin de hoos zich voortbewoog; in de twee buitenste stroken liggen ze schuin, naar de centrale strook toe. Blijkbaar ontstond daar de wind door samen- | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 284]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
stelling van de radiaal toestromende lucht met de voortschrijdende beweging (fig. 139). Als men nauwkeuriger waarneemt, vindt men dikwijls een zekere asymmetrie tussen de twee zijstroken: a) de linker is minder scherp begrensd dan de rechter, en dikwijls slechts door zeer weinig bomen vertegenwoordigd; b) de richting van de bomen in de linkerstrook vormt een grotere hoek met de bewegingsrichting dan in de rechter. Deze verschillen bewijzen dat de lucht niet eenvoudig radiaal naar de voet van de hoos stroomt, maar dat er ook een draaiingsrichting in was, waarvan de samenstelling met de andere stromingen de waargenomen asymmetrie geheel verklaart. Het is dus duidelijk dat nabij het oppervlak van de grond de lucht in hoofdzaak naar de hoos toe stroomt, en slechts in geringe mate roteert. - Dikwijls is de regelmaat veel minder mooi dan we 't hier hebben geschetst, doordat het stelsel der luchtstromen blijkbaar ingewikkelder was. Men kan het werk bekorten door het opnemen langs dwarslijnen. Op een goed kenmerkend punt trekt men een lijn dwars op de baan, en tekent nu alleen die bomen waarvan de wortels ten hoogste 4 m van die lijn verwijderd zijn; bij gekruiste, op elkaar liggende bomen wordt alleen die getekend welke het meest in de richting van de naburige ‘normale’ stammen ligt. Dergelijke dwarsopnamen voert men bij verschillende interessante punten der baan uit. Zeer mooie windbanen vindt men in korenvelden, waarvan meestal de neergeworpen aren als echte ‘krachtlijnen’ gerangschikt zijn. 3. Vervolgens verzamelen we alle aanwijzingen die we kunnen vinden omtrent voorwerpen die door de hoos vervoerd en een eind verder neergevallen zijn. De berichten die men hierover verneemt zijn wel belangwekkend, maar de hoofdzaak ontbreekt gewoonlijk: de nauwkeurige aantekening op de landkaart van de punten waar elk voorwerp vandaan gehaald en tenslotte terecht gekomen is. In vele gevallen vindt men door het onderzoek ter plaatse dat er banen van 10 of 20 km lengte en meer beschreven zijn, altijd aan de linkerzijde van de hoosbaan, dikwijls echter sterk afwijkend van richting, zodat men wel moet aannemen dat de hoos aan haar boveneind door een lange horizontale wervel werd voortgezet. Van de 258 Europese hozen wier beschrijvingen door Wegener bewerkt zijn, was er maar één waarbij behoorlijk gelet was op deze zo merkwaardige transportverschijnselen! Gevallen van ‘visregen’ of ‘kikvorsenregen’ zijn natuurlijk bijzonder belangwekkend (vgl. II, § 153). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 285]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4. Bepaal volgens de mondelinge berichten het gebied waar regen en hagel gevallen zijn. Gewoonlijk is de hoos aan de rand van dit gebied ontstaan. Aan de vóór- of aan de achterkant? Links of rechts? Vormde de hoos zich vóór de regen (of hagel) viel, of later? - Deze inlichtingen hebben groot belang, omdat Wegener dacht dat de hozen gevormd worden door de kraag van de hagelbui, die zich als een lange horizontale wervel uitstrekt, en waarvan de uiteinden naar beneden buigen (fig. 140); aan de voorkant van de bui zou de lucht opwaarts wervelen,
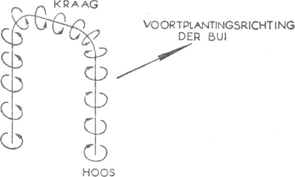 Fig. 140. Schematische voorstelling van een hoos als uiteinde van een werveldraad (volgens de oude theorie van Wegener, 1911).
en daaruit zou dan volgen dat hozen rechts van het onweergebied in de richting van het uurwerk moeten draaien; links omgekeerd. De waarnemingen schijnen veeleer op het tegendeel te wijzen, hetgeen door Professor van Everdingen toegeschreven is aan een snel met de hoogte toenemende windsterkte;Ga naar voetnoot1) de draaiingszin van de werveling zou dan juist het omgekeerde zijn van wat in fig. 140 getekend is. Wegener heeft thans die opvatting overgenomenGa naar voetnoot2). - Hozen links van het onweergebied komen zelden voor. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
177. De lengte van stoompluimen en de uitwisselingsconstante van de dampkring.Ga naar voetnoot3)De lengte van de stoompluim van een lokomotief is soms groter, soms kleiner, en het is belangwekkend om na te gaan van welke faktoren die lengte afhangt. De concentratie van de waterdamp in de omgevende lucht zij s; de stoomtoevoer verhoogt de waterconcentratie tot s + Δs, zodat de lucht verzadigd | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 286]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
wordt en een wolkvormig neerslag van waterdruppeltjes vertoont. Nu verspreidt zich de stoom door de wervelingen van de dampkring, de concentratie van het water neemt af naarmate we ons verder van de lokomotief verwijderen, de waterdruppeltjes verdampen weer, en waar de lucht net niet meer verzadigd is houdt de stoompluim op. Tevens zou ook moeten bedacht worden, dat de temperatuur der lucht door de stoomtoevoer verhoogd was; maar dit blijkt slechts van geringe invloed te zijn. Men kan aantonen dat de waterdamp zich op zulk een wijze verspreidt, dat zijn concentratie in de as van de rookpluim aldus met de afstand r afneemt: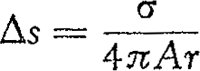 . Hierin is σ de luchtmassa waarvan de dampdruk door de stoomtoevoer met 1 mm per sekunde verhoogd kan worden; A is de uitwisselingsconstante, die een maat is voor de dooreenroering van de lucht. Dan geldt dus aan het uiteinde der stoompluim: 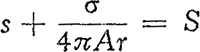 (= verzadigingsdruk), of 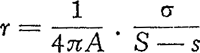 . De lengte der stoompluim is dus omgekeerd evenredig met de uitwisselingsconstante en met het verzadigingstekort; was de lucht buiten al met waterdamp verzadigd, dan werd de stoompluim oneindig lang. Die lengte hangt echter niet af van de treinsnelheid noch van de windsnelheid; de lengte der stoompluimen van twee treinen die de ene met, de andere tegen de wind rijden, moet gelijk zijn. Wel zal bij sterke wind de stoompluim korter zijn, maar alleen tengevolge van de grotere werveligheid A. Een lokomotief in volle vaart verbruikt ongeveer 2 kg water per sekunde en zet die om in waterdamp. Deze heeft ten opzichte van lucht een soortelijk gewicht 0,60, in normale omstandigheden van druk en temperatuur; verspreidt hij zich dermate, dat zijn drukking afgenomen is tot 1 mm, dan is zijn dichtheid ten opzichte van lucht slechts 0,60/760. Dus kan 1 g water de dampdruk van 760/0,60 g lucht met 1 mm verhogen, en zo wordt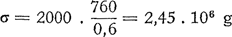 . Voor een verzadigingstekort van 1 mm en A = 1 (zeer rustige lucht) zou de lengte 1940 m worden, wat wel aannemelijk is. In 't algemeen is A op enige meters hoogte van de orde 10 tot 100. Uit de damppluim van een stoomboot werd bepaald A = 12. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 287]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Doe een aantal bepalingen van r en S - s, dit laatste met behulp van de psychrometer, II § 94; bereken telkens de uitwisselingsconstante uit:
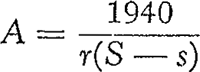 , waar r in m, S en s in mm kwik zijn uitgedrukt. Het is voldoende wanneer men de orde van grootte vindt van deze moeilijk te bepalen constante. Zij is van het grootste belang voor de verspreiding van stofdeeltjes, van radioaktieve stoffen, van warmte, enz. in onze dampkring. De uitwisselingsconstante van de dampkring op een gegeven ogenblik hangt in hoofdzaak af van de graad van turbulentie, van werveling die de luchtmassa's door elkaar roert. De gehele stemming van het landschap ondergaat daar de invloed van. - Vergelijk de zacht gebogen lijn van de rookzuil, die bij rustige maannacht uit een schoorsteen opstijgt, met de golvende, kronkelende lijnen van de rookpluimen bij dag, ook al is de wind slechts matig sterk; bekijk ook de voortdurende snelle vervormingen bij stormwind. Bedenk daarbij, dat het niet de windsnelheid zelf is, die deze vervormingen teweegbrengt, maar het onderlinge snelheidsverschil tussen de naburige volumeelementen der bewegende luchtlaag. U ervaart dus, dat de turbulentie in 't algemeen tegelijk met de windsnelheid toeneemt, maar volstrekt niet altijd. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
178. Adempluimen.In de winter zien we hoe onze adem bij het uitademen tot een nevel van fijne druppeltjes verdicht wordt. Bij warme, droge lucht is de adem niet zichtbaar; er zijn allerlei overgangen, en men kan uit vorm, grootte en dichtheid van de adempluim iets over de vochtigheidsgraad der lucht zeggen. Du Bois Reymond bemerkt, dat de adempluim beter zichtbaar wordt als men de lucht eerst zo sterk mogelijk in de borstholte samengeperst houdt, en dan ineens de mond opent. Door de plotselinge ‘adiabatische’ uitzetting wordt de uitgeademde lucht afgekoeld en de waterdamp condenseert, vooral als er stofkernen in de buurt zijn. Dit belangrijke verschijnsel is dus zonder enig toestel rechtstreeks aan te tonen! De waarneming gelukt het best op dagen waarop de adempluim net zichtbaar is en goed door de zon verlicht wordt. Laten we eens beproeven de formule voor de lengte van stoompluimen op de zoveel kleinere adempluimen toe te passen. Bij een gewone uitademing, die misschien ⅓ sec duurt, doen we ongeveer 0,5 1 lucht uitstromen die verzadigd is bij lichaamstemperatuur (37o); de waterdamp in die ademhalingslucht | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 288]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
heeft dus een spanning van 47 mm en weegt
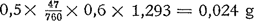 . In onze formule wordt nu 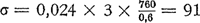 . Dus: 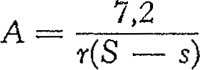 . Als dus de adempluim bv. 36 cm lang is, bij een verzadigingstekort van 1 mm, moet men besluiten dat A = 0,2. In het algemeen vinden we waarden van 0,1 tot 1, die aanwijzen dat de lucht in de eerste meters boven de grond zeer rustig is en weinig wervelingen vertoont. We moeten er ons echter wel rekenschap van geven dat het zeer gewaagd is de formule tot zulke korte stoompluimen uit te breiden, en dat we niet veel meer kunnen verwachten dan een ruwe benadering. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
179. Reukwaarnemingen.Wie het landschap buiten heeft genoten, weet hoezeer de geuren in al hun verscheidenheid tot het vormen van de stemming bijdragen. Ozon of stikstofoxyden ruikt men na sterke onweders. Waterdamp zou een reeks eigen geuren hebben, afhankelijk van zijn concentratie (zijn dit niet veeleer verschillende verontreinigingen?). Bloemengeuren ruikt men in de zomermaanden. Een zeer eenvoudige en doeltreffende indeling der natuurgeuren is gegeven door W. HellpachGa naar voetnoot1):
De ‘waterdampgeuren’ worden door DreisGa naar voetnoot2) op de volgende wijze onderverdeeld:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 289]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
De bloemengeuren zijn (alweer volgens Dreis) in een dergelijke schaal te rangschikken.
In deze rangschikkingen moge wat fantasie zijn en een zeker persoonlijk element. Maar ook een aantal juiste waarnemingen zijn erin verwerkt! Wie twijfelt moge daarom beginnen met zelf aandachtig en stelselmatig waar te nemen, en vorme zich dan een eigen oordeel. Bloemengeur ruikt men het sterkst bij temperaturen van 5o tot 15o 's morgens en 's avonds, van Mei tot September. Eerst overheerst de meidoorn, in Juni de vruchtbomen en tuinheesters, in Juli het hooi (toe te schrijven aan cumarine), later de bloeiende linden en de klaver op de wei, nog later de lupine op de velden. De geur van het bos is iedereen bekend. Hij is anders bij vochtig dan bij droog weer; dennebossen geuren bijzonder sterk als het geregend heeft en de zon daarna schijnt. Hij is ook anders volgens de samenstelling der flora; bijzonder fris ruikt het eikenhakhout. Tenslotte hangt hij af van het jaargetij, waarschijnlijk vooral door de grotere of kleine hoeveelheid afgevallen bladeren. De geur van de zee is uiterst kenmerkend. Is het jodium? of ozon? Of de ontbindingsprodukten van wat de zee op het strand werpt? Het is sedert lang bekend dat bij dalende barometer de grachten | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 290]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
en greppels van grote draineerwerken beginnen te ruiken. Dit schijnt hetzelfde verschijnsel als de bekende geur van vochtige aarde, die het plotseling invallend regenweer aankondigt. De verklaring zal wel zijn, dat de lucht die in de spleten en poriën der aarde zat dan voor een deel daaruit weggezogen wordt door de verminderde drukking. Dat zulk een effekt niet denkbeeldig is blijkt uit de blazende putten (§ 146). Van de natuur- en scheikunde dezer reukstoffen is zeer weinig bekend. Onze organen hebben hiervoor een graad van gevoeligheid, die door geen meettoestel geëvenaard werd.
Hoe die buitelende wind, die naar het hooi rook van den zomer, verfrischte. Blank lag het veld, ...
Aart van der Leeuw, Sneeuw (Vertellingen).
Het nat haalde al de bloemreuken omhoog.
De scherpe reuk van 't open veld.
De kalme reuk der aarde.
Reuk van water, hooi en vlier.
De natte hof, waaruit de regen den zoetsten rozenreuk omhoogsloeg.
De reuk der platte aarde, die sedert dagen en dagen beregend was.
Timmermans, Pallieter, blz. 36, 55, 92, 116, 150.
Men wordt weer een wilde bij de geur van het woud.
Sully-Prudhomme.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
180. De vallende sterren en de hoogste dampkringslagen.Ga naar voetnoot1)
Zoals men langs den heldren avondhemel
Somwijlen plotseling een vonk ziet schieten,
De ogen trekkend, die stil vóór zich zagen -
Het lijkt een ster, die van haar plaats wil vlieden.
Dante, Paradiso, XV, 13-16.
Iedereen kent de ‘vallende sterren’. Men ziet ze op de meest onverwachte wijze soms hier, soms daar aan de hemel oplichten, een lichtlijntje trekken, en weer verdwijnen. Het zijn geen sterren, het zijn kleine korreltjes, misschien een speldeknop groot, die veel vlugger dan een kanonkogel uit de wereldruimte aankomen, door onze dampkring vliegen, en daarbij door de grote snelheid waarmee ze tegen de luchtmolekulen botsen tot lichten gebracht | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 291]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
worden. Op bepaalde tijdperken van het jaar komt de Aarde door zwermen van die stofjes, en kan men soms een ‘sterrenregen’ waarnemen, waarbij alle banen schijnen uit te stralen van één bepaald punt aan de hemel: dat is natuurlijk een perspektief-verschijnsel, juist zoals de wolkenbanden (II § 130), het watertrekken der zon (I § 193), enz.; al die banen zijn eigenlijk evenwijdig.
Sommige zwermen zijn gekenmerkt door korte banen, andere door lange; sommige door langzaam bewegende meteoren, andere door snelle. De kleuren zijn de ene maal meer blauwgroen, de andere maal meer rood, oranje of geel; van de zwakste meteoren is het licht onvoldoende om een kleur te laten onderscheiden. Een waarnemer beweert ‘sissen’ te hebben gehoordGa naar voetnoot1): dat lijkt zeer onwaarschijnlijk, veeleer is dit een dergelijke begoocheling als bij 't poollicht (II, § 223). Van ons standpunt stellen we vooral belang in de vallende sterren, omdat ze ons iets leren betreffende de buitenste lagen van onze dampkring en de grootste hoogten waar er nog een spoor van die dampkring overblijft, zij het ook zo ijl, dat die door geen andere verschijnselen aangetoond kan worden. - Het heeft tot in 1798 geduurd eer men iets te weten is gekomen over de ware hoogte waarop de vallende sterren oplichten. Twee jonge studenten der universiteit te Göttingen, Brandes en Benzenberg, besloten op eigen houtje waarnemingen te doen, en slaagden erin zonder enig hulpmiddel deze belangwekkende vraag op te | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 292]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
lossen. Om hun werkwijze na te volgen, spreken we met een vriend af dat we op een bepaalde avond samen zullen waarnemen; we zetten onze horloges zo nauwkeurig mogelijk gelijk, begeven ons op een afstand van bijvoorbeeld 50 km van elkander, en tekenen nu zorgvuldig op een sterrekaart de banen van alle vallende sterren die we binnen een vooruit afgesproken stuk van de hemel waarnemen, daarbij de juiste waarnemingstijden vermeldend. Vooral de hemel loodrecht op de verbindingslijn van de twee waarnemers moet bewaakt worden. - Na afloop vergelijken we onze aantekeningen, zoeken of er volgens de waarnemingstijden vallende sterren bij geweest zijn die we allebei
 Fig. 141. Spoor van een vallende ster, gezien van uit twee verschillende waarnemingspunten.
hebben gezien, en onderzoeken of we hun banen verschoven hebben gezien ten opzichte van de sterren (fig. 141). Voor sterren in richtingen loodrecht op de verbindingslijn is de hoogte der baan dan: 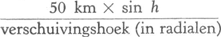 , als h de hoogte boven de gezichteinder voorstelt. De twee Göttinger waarnemers vonden hoogten van 52 tot 170 km, en deze orde van grootte is ook later telkens bevestigd; slechts in heel zeldzame gevallen heeft men vallende sterren reeds op een hoogte van 400 km zien lichtgeven. Voor de uitvoering dezer waarnemingen is het van belang te weten, dat men de meeste kans heeft vallende sterren waar te nemen in de herfst en na middernacht; men ziet er dan gemiddeld 10 tot 20 per uur. Nog gunstiger zijn natuurlijk de nachten waarin bepaalde zwermen optreden. In de tabel blz. 291 vindt men de belangrijkste zwermen, met de datum waarop ze meestal zichtbaar zijn. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 293]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
181. VuurbollenGa naar voetnoot1) - (Plaat XIV).Vuurbollen zijn verwant met vallende sterren, maar veel groter en veel zeldzamer. Het zijn echte stenen, soms rotsblokken, die in de dampkring der aarde doordringen, gloeien en lichtgeven, een enkele maal zelfs op Aarde neervallen eer ze verdampt zijn. Dikwijls is het licht zo sterk, dat men de vuurbol in 't volle daglicht ziet; soms spat hij uiteen met een knal en gedonder. De lichtverschijnselen langs zijn baan zijn van groot belang voor onze kennis van de hoogste dampkringslagen, en het minutenlang nalichtende spoor van grote vuurbollen geeft ons gewichtige aanwijzingen over de luchtstromen op die grote hoogten. Men is overeengekomen de naam van ‘vuurbollen’ voor te behouden voor lichtverschijnselen helderder dan Jupiter, terwijl men de zwakkere ‘vallende sterren’ noemt; maar een scherpe grens is er natuurlijk niet. Vuurbollen zijn zó zeldzaam, dat het geen zin heeft die stelselmatig te beproeven waar te nemen. We zijn aangewezen op de tegenwoordigheid van geest van toevallige ooggetuigen, en moeten dus trachten het grote publiek zoveel mogelijk in te prenten wat er in zulk een geval waar te nemen valt. Hoofdzaak is altijd het bepalen van de ware baan. Dit is mogelijk als dezelfde vuurbol van verschillende plaatsen uit gezien is. Hier volgen de voorschriften waar de waarnemers op te letten hebben.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 294]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
In 't algemeen geve men zo uitvoerig mogelijk aan wat men gezien heeft en hoe men tot zijn schatting gekomen is. Het verder berekenen is nu zaak van de naastbijgelegen sterrewacht, waarvan de astronomen ons later wel zullen weten te vertellen hoe hoog onze meteoorsteen vloog. Men vindt, dat de hoogte van het punt waar de vuurbol begint op te lichten gemiddeld 140 km bedraagt, de hoogte van het uitdovingspunt 50 km, maar deze getallen kunnen tussen ruime grenzen variëren. Het lichtgeven van vallende sterren en vuurbollen is te verklaren door de botsingen der luchtmolekulen tegen het snel bewegende steentje; dit omhult zich met een dampmantel, die de voornaamste bron van de uitgezonden straling wordt. Bij grotere stenen, die als vuurbollen waargenomen worden, kan de lucht vóór de meteoriet niet intijds uitwijken, zij wordt adiabatisch samengeperst en verhit. Buitengewoon belangwekkend is het nalichten van het spoor. Bij een vallende ster ziet men zulk een nalichten dikwijls gedurende breukdelen van een sekunde; maar hier kan het minuten, tot een uur toe bedragen! Meestal is het slechts het middengedeelte der baan die nalicht, tussen 80 km en 100 km; het is zaak bij de beschrijving nauwkeurig aan te geven wat betrekking heeft op de baan zelf en wat op het veel kortere nalichtende gedeelte. Een dergelijk verschijnsel als dit nalichten treedt op bij bepaalde proeven in het laboratorium met zeer verdunde gassen (druk: 0,1 mm), bijvoorbeeld als stikstofatomen in ionen ontleed zijn en zich weer met de elektronen verenigen. Hoe lager de druk, hoe langer het duurt eer elk ion een ‘kameraad’ ontmoet heeft, en over hoe langer tijd zich het lichten uitstrekt. Het lichtspoor is meestal vrij breed en buisvormig, hetgeen blijkt uit de vele waarnemingen van ‘dubbele’ sporen: aan de | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 295]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
randen van de buis ziet de waarnemer een dikkere laag lichtend gas dan in het midden. Het neemt snel in dikte toe en kan na 10 min. wel al 1o breed zijn (2 maal de diameter der maan, meer dan 1 km dikte!). Zonder twijfel is dit een diffusieverschijnsel dat opnieuw op de lage drukking wijst. Men kan rechtstreeks zien dat de drukking met toenemende hoogte afneemt, want het spoor verbreedt sneller bij het begin- dan bij het eindpunt, en neemt geleidelijk de vorm aan van een uitroeptekenGa naar voetnoot1). Dikwijls bemerkt men ondertussen ook krommingen en kronkels die sterker en sterker worden, en die wijzen op turbulentie in deze hoge lagen (Plaat XIV); de dampkring is daar dus niet zo rustig als men menen zou, en het wordt begrijpelijk dat de aldus dooreengeroerde gassen op alle hoogten vrijwel dezelfde samenstelling hebben als hier beneden. Door het nalichtende spoor ten opzichte van de omringende sterren te tekenen en van minuut tot minuut te volgen, vindt men de verplaatsing in hoekmaat; met behulp van de ware hoogte, door de astronomen berekend, volgt daaruit de snelheid der luchtstromingen in deze hoogste dampkringslagen. Men heeft aldus gevonden dat er boven de 80 km een algemene stroming van West naar Oost is, met een snelheid van de orde van 150 km/uur. Er zijn ook enige zeldzame gevallen bekend van vuurbollen die men bij dag heeft gezien of in de schemering, verlicht door de stralen der ondergegane zon. Ze laten een spoor van rook, als een wollen draadje dat dikker wordt en meestal gaat kronkelen. Deze sporen zijn niet langer dan een kwartier gevolgd kunnen worden, maar dit is voldoende geweest om uit te maken dat ze zich op een hoogte bevinden van 30 tot 80 km, en dat de stroming daar van Oost naar West gericht is. Beneden de 25 km kennen we de wind uit waarnemingen met loodsballons: daar is de algemene stroming weer van West naar Oost gericht. Men ziet hoe belangwekkend de gegevens zijn die men uit waarnemingen van vuurbollen kan verkrijgen! Vooral voor de laag van 30-80 km, die met dagmeteoren moet worden verkend, is aanvulling van ons materiaal zeer gewenst: er zijn maar een kleine 20 gevallen bekend. |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||