Wisconstighe gedachtenissen. Deel 1: van 't weereltschrift

Nv van Mercvrivs breede.

1 Lidt.
Inhoudende Ptolemeus dadelicke gagheslaghen ervaringhen van Mercuriusloop.

Om beuqamelicker te verclarē Ptolemeus dadelicke gageslagē ervaringen der gedaēte vā Mercurius breedeloop mette somme vā sijn spiegeling daer op veroirdent,



so laet A B C dē inrontwech beteyckenen, diens middelpunt is E, dē vasten Eertcloot F, deur welcke en oock deur E ghetrocken sy de lini C F E A, soo dat A t'verstepunt is, C t'naestepunt, en deur F ghetrocken wesende de lini B F D rechthouckich op A C, so bedien de twee punten B, D, des wechs 90 tr. en 270 tr. en hoewel dat so veel verschilt als de uytmiddelpunticheyt E F veroirsaeckt, nochtans angesien Ptolemeus de selve twee punten den 90 en 270 noemt, wy sullenser voor nemen, daer na sy opt punt D als middelpunt beschreven het inront G H I K, diens verstepunt G, naestepunt I, en middelverheden H, K, tusschen welcke vier punten gheteyckent sijn de twee middellijnen I G, H K.

Dit aldus wesende, soo heeft Ptolemeus deur dadelicke ervaring bevonden dat Mercurius meeste breede op de zuytsijde was van 4 tr. 5 ①, ghebeurende altijt

[p. 312]

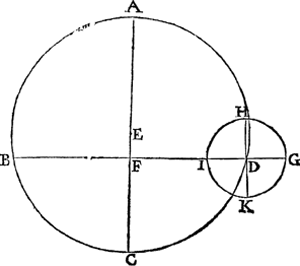
als sijn inronts middelpunt was 90 tr. van sijn wechs verstepunt, soo wel ter eender als ter ander sijde, dat is soo wel inden 270 tr. an D, als inden 90 an B (welcke 90 tr. is onder des duysteraers 280 tr. gemerckt deur de Byeenvouging des 13 voorstels deses 3 boucx, het verstepunt onder des duysteraers 190 tr. is) en Mercurius in des inronts naestepunt als an I: Maer buyten het naestepunt wesende, soo was sijn zuydersche breede voor datmael cleender, en ten minsten doen hy also ant verstepunt G was. D oirsaeck waerom de boveschreven breeden even vallē als het inronts middelpunt is an D of B, blijckt inde form, om dat de lini vanden Eertcloot F tot D, even is ande lini van F tot B: Want daer uyt volght dattet inronts middelpunt an B wesende, sijn verstepunt en naestepunt in sulcken ghestalt uyt den Eertcloot F ghesien worden, als wanneert an D is.

Ten tweedē so bevant hy op de noortsijde de meeste breede van 1 tr. 45 ①, ghebeurende altijt als sijn inronts middelpunt was 90 tr. vā sijn wechs verstepunt, soo wel ter eender als ter ander sijde, en Mercurius an sijn inronts naestepunt, maer buyten het naestepunt wesende, soo was sijn noordersche breede voor datmael cleender, en ten minsten doemē hem alsoo ant verstepunt vandt.

2 Lidt.
Inhoudende Ptolemeus spiegheling ghetrocken uyt de voorgaende dadelicke ervaringhen des 1 lidts.

Anghesien Ptolemeus voorgaende ervaringhen, noch breeder connen verclaert worden deur sijn spieghelinghen die hy daer op verdocht heeft, soo sal ick de somme van dien hier by voughen als volght.

Nadien des inrontwechs twee punten die uyt den vasten Eertcloot F inde meeste breede ghesien worden sijn B en D, soo soude daer uyt volghen dat de ghemeene sne van die wech en den duysteraer, rechthouckich moet commen op B D, ende want Ptolemeus sich in aller Dwaelders breedeloopen voorstelde die te gaen deur den Eertcloot F, soo soude volgens die oirden de lini A F C de duysteraersne moeten sijn, en daerom het inronts middelpunt wesende an A of C, en Mercurius ant inronts verste of naestepunt, soo soude hy uyt den Eert cloot F moeten gesien worden int plat des duysteraers sonder breede: Maer de ervaring wees hem anders, want hy doē sijn breede altijt bevant vā 45 ① na t'Zuyden: Sulcx dat hy daerom (benevens noch een ander redē daer inden Byvough des breedeloops met stelling eens vasten Eertcloots af geseyt sal worden) Mercurius spiegheling anders veroirdende als vande drie bovenste Dwaelders, t'welck aldus toeginck: Hy heeft gheseyt de lini B D streckende deur de twee punten der uyterste afwijcking, te wesen de ghemeene sne des inrontwechs en duysteraers, teghen de natuerlicke reghel: Maer weerom ter ander sijde gaf den inrontwech en het inront seker drie seer versierlicke wagghelende roersels, die onderscheyts halven ghenoemt worden^* afweging,^* afwijcking, en^* afkeering, waer me hy tot sijn voornemen gherocht, waer af ick oock van elck int besonder verhael sal doen, dat treckende uyt de bepalinghen die Purbachius tot dese plaets van dit roersel verstandelick doet.

Om dan mette^* afweging te beginnen, soo is te weten dat Ptolemeus den inrontwech gheseyt heeft op B D als as een wagghelende roersel te hebben overentweer gaende of waggelende als de balck eens waeghs, ghenoemt afweging, sulcx dattet inronts middel punt wesende an B of D, soo en isser gheen afwe-

* Deviatio.

* Declinatio.

* Reflectio.

* Deviatio.

[p. 313]

ging, maer is des wechs heel plat int plat des duysteraers: Daer na het inronts middelpunt van B of D vertreckende, soo begint den wech af te weghen, of te neyghen altijt na het Zuyden, en vermeerdert dese afweging gheduerlick tot dattet inronts middelpunt ghecommen is ant verstepunt A, of naestepunt C, en dan is de afweging ten grootsten vande boveschreven 45 ①; Welck daer na weerom vermindert, tot dattet inronts middelpunt ghecommen is an B, of D, alwaer dan weerom gheen afweging en is. En blijckt hier uyt dattet roersel t'welck het inronts middelpunt vande afweging ontfangt nummermeer op de noortsijde en gheschiet.

Maer om nu vande^* afwijcking te segghen, soo is te weten dattet plat des inronts deur een waggelende roersel afneyght vant plat sijns wechs op tweederley wijse: Ten eersten met afwijcking op de middellijn H K, streckende deur de middelverhedē H, K: Met dit roersel gebeuret dat de middellijns I G verstepunt G, op d'een sijde des wechs afwijckt, en t'naestepunt I op d'ander. Dese afwijcking houdt dusdanige reghel: Wanneer des inronts middelpunt als D, is an des wechs verstepunt A, de voorschrevē middellijn I G is in t'plat des wechs: Maer het inronts middelpunt van t'verstepunt A vertreckende, so begint des inronts verstepunt af te wijcken na het Zuyden, ende het naestepunt na het Noorden, welcke afwijcking geduerlick vermeerdert tot dat des inronts middelpunt ande middelverheyt B gecommen is, en alsdan gebeurt de middellijns als I G meeste afwijcking, welcke daer na gheduerlick vermindert, tot dattet middelpunt des inronts is an des wechs naestepunt C, alwaer de voorschrevē middellijn als I G wederom geen afwijcking en heeft, maer het inronts middelpunt van C vertreckende na de middelverheyt D, het verstepunt als G begint af te wijcken van t'plat des wechs na het Noorden, en het naestepunt gelijck I na het Zuyden, en vermeerdert die afwijcking geduerlick tot dat des inronts middelpunt ant uyterste D gecommen is, alwaer die afwijcking weerom ten grootsten wort. Van daer voort vermindertse tot dattet inronts middelpunt an t'verstepunt A is, alwaer gelijck int begin de voorschrevē middellijn als I G, weerom int plat des wechs is: En daer na volgt weerom d'eerste gestalt. Vyt t'gene geseyt is blijct dat des wechs afweging tē grootstē sijnde, so heeft het inront geen afwijcking, maer de wech sonder afweging wesende, dat dā des inronts afwijcking tē grootstē is.

Nu rester noch de^* afkeering te verclaren welcke dusdanich is: Des inronts plat heeft boven de voorschreven waggeling op den as H K, noch een ander op den as I G tusschen des inronts verstepunt en naestepunt (ghenouchsaem toegaende gelijck de tweederley waggeling die het zeecompas ontfangt, met twee assen op malcander rechthouckich commende) deur welck roersel gebeurt dat de middellijn H K het plat des wechs deursnijt inde lini I G als gemeene sne, so dat des inronts slincker helft op d'een sijde des inrontwechs, de rechter helft op d'ander sijde af keert: Dese middellijns af keering houdt dusdanige regel: Wanneer des inronts middelpunt is ande middelverheyt D, soo en heeft de voorschreven middellijn H K geen afkeering vande wech A B C D, dan is int plat der selve: Maer het inronts middelpunt van D vertreckende na het verstepunt A, soo begint de middellijns slincker helft H D af te keeren na het Zuyden, de ander helft na het Noorden, welcke afkeering geduerlick vermeerdert tot dattet inronts middelpunt ant verstepunt A ghecommen is, alsdan ten grootsten wesende. Daer na voortgaende na het ander punt B soo vermindertse weerom tot datser an gecommen is, alwaer weerom geen af keering en gheschiet. Maer het inronts middelpunt van die plaets vertreckende na het naestepunt C, so begint de voorschreven slincker helft ghelijck H D weerom af te keeren na het

* Declinatione.

* Reflectio.

[p. 314]

Noorden, en vermeerdert alsoo tot datse ant naestepunt C is, alwaermense dan weerom ten grootsten bevint: Van daer vermindertse geduerlick tot dattet inronts middelpunt comt an d'ander middelverheyt D, alwaer weerom geen afkeering en is, en alsdan begint weerom de voorgaende gestalt. Hier uyt is kennelick dat ter plaets des inrontwechs daer het inront geen afwijcking en heeft, sijn meeste afkeering te ghebeuren.

3 Lidt.
Inhoudende verclaring vā Mercurius breedeloop met stelling eens roerenden Eertcloots.

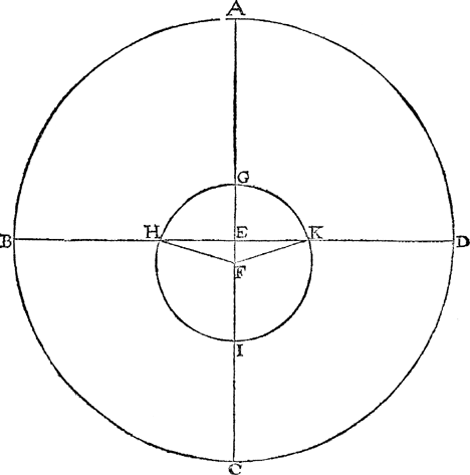
Hier vooren beschreven sijnde het 1 lidt inhoudende Ptolemeus dadelicke ervaringen (waer by tot breeder verclaring noch vervought wiert het 2 lidt van sijn spiegeling) men soude deur vervouging der selve ervaring op stelling eens roerenden Eertcloots volgens de voorgaende gemeene regel tottet begheerde commen, nochtans angesien de form vande onderste Dwaelders binnen den Eertclootwech loopende, wat anders valt als vande bovenste, en dat Mercurius wech niet deur des Eertclootwechs middelpunt en strect, t'welck voor de sommige verclaring mocht vereysschen, soo sal icker wat af seggen. Laet A B C D

[p. 315]

den Eertclootwech beteyckenen, diens middelpunt E, Mercuriuswechs middelpunt F, waer op beschreven is sijn wech G H I K, daer na deur E en F ghetrocken de middellijn A C, en deur t'punt E de lini B D rechthouckich op A C, soo is I t'punt verst van des Eertclootwechs middelpunt E, en G het naestepunt: Voort anghesien Ptolemeus bevonden heeft dat Mercurius meeste breeden altijt gebeurden als het inronts middelpunt was by de middelverheden, so volght daer uyt met stelling eens roerendē Eertcloots, dat de selve meeste breedē altijt gesien worden als Mercurius is an sijn wechs middelverheden H en K, en den Eertcloot an B of D: Nu dan H en K wesende de twee puntē welcke in Mercuriuswech de grootste afwijcking crijgē diemē uyt den Eertclootwech sien can, soo seggen wy dier twee platten gemeene sne te moeten commen rechthouckich op B D, dats in G I, of evewijdich mette selve, en niet in H K gelijck Ptolemeus die stelt: Maer om nu te vindē waer de selve duysteraersne valt, metsgaders Mercuriuswechs afwijcking van t'plat des duysteraers, ghelijck van Saturnus int 21 en 22 voorstel ghedaen wiert, ick souck voor al de langde der lini H K, tot dien eynde aldus segghende: De driehouck E K F heeft drie bekende palen, te wetē Mercuriuswechs halfmiddellijn F K 3572, en de uytmiddelpunticheytlijn E F 947 deur de Byeenvouging des 13 voorstels deses 3 boucx, en dē houck

K E F recht: Hier me gesocht de sijde EK, wort bevonden deur het 5 voorstel der platte driehoucken van	3444.
Daer toe noch soo veel voor E K, comt voor de begheerde H K	6888.
En van E D 10000, ghetrocken E K 3444 eerste in d'oirden, blijft voor de lini K D, oock me voor H B	6556.
Dit aldus bekent sijnde ick teycken een ander form als gedaen wiert met Saturnus int 22 voorstel, treckende ten eersten L M als Eertclootwech overcant ghesien, even an B D 20000, en stel int middel van L M t'punt N als Eertclootwechs middelpunt, ick treck daer na de lini OP van 6888 even an H K tweede in d'oirden, en sniende L M in Q, daer na L O evē met H B 6556 derde in d'oirden, sgelijcx M P even met K D, dats oock doende 6556, en segh den houck O L Q te doen 1 tr. 45 ①, en P M Q 4 tr. 5 ① volghens d'ervaring int 1 lidt: Dit soo wesende de cruysvierhouck L O M P heeft vijfbekende palen, te wetē L M 20000, L O 6556, M P 6556, den houck O L Q 1 tr. 45 ①, en den houck P M Q 4 tr. 5 ① deur t'ghegheven. Merckt noch dat benevens de boveschrevē vijf palen tot meerder gerief bekent sijn drie ander, te wetē OP 6888, P L 13444 als even genouch sijnde met OP 6888 en O L 6556 t'samen, voort O M doende oock soo veel: Hier me ghesocht den houck O Q L, wort bevonden deur het 6 voorstel inde Byvough der platte veelhoucken voor Mercuriuswechs begheerde afwijcking vanden duysteraer	5 tr. 32 ①.
En de lini Q M van 11364, waer af ghetrocken M N 10000, blijft voor de lini vande duysteraersne Q totten Eertclootwechs middelpunt N.	1364.

Tot hier toe is beschreven t'ghene ick van Mercurius int besonder verclaren wilde. Belanghende ander byvallen als inde ses voorstellen van Saturnus breede beschreven sijn, die houden wy als voor ghemeene reghel over Mercurius en d'ander Dwaelders te verstrecken.

Angaende overeencomminghen en verschil deser stelling van Mercurius

[p. 316]

breedeloop met die van Ptolemeus, daer af sal gheseyt worden inden volgenden Byvough des breedeloops met stelling eens vasten Eertcloots.