Ideën II

[p. 317]

529.

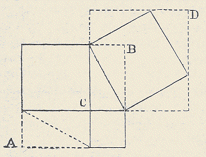Ik vond onlangs een nieuw bewys voor de stelling van Pythagoras. Hier is het. Door, als op nevenstaand voorbeeld, zes driehoeken te construeeren - ieder gelyk aan den geheven rechthoekigen driehoek - verkrygt men twee gelyke kwadraten, A B en C D. ^* Als men van elk dezer figuren vier driehoeken aftrekt, bewyst de gelykheid van 't overschot aan weerszy, wat er te bewyzen was.

Eenvoudiger kan het niet, dunkt me. Na dit bewys gevonden te hebben, vernam ik dat er een werkje bestond, waarin dit onderwerp werd behandeld. Ik schafte my dat boekjen aan ^† en vond er myn demonstratie niet in. Ook meen ik dat geen der daarin voorkomende bewyzen zoo aanschouwelyk en helder is als 't myne. Wie beweren mocht dat het reeds vroeger was gevonden, zou me verplichten met de opgave waar 't gepubliceerd is? ^§ Professor Hofmann kende 't niet, en ook Strootman zou er wel melding van gemaakt hebben, als 't hem bekend ware geweest. Hofmann schynt een speciale studie te hebben gemaakt zoowel van de propositie zelve, als van de litteratuur over dit onderwerp.

Ik hoop dat niemand vragen zal welk nut het heeft, te zoeken naar eenvoudiger bewyzen voor 'n bekende waarheid? Dit streven leidt tot helderheid van opvatting, en gewent ons aan duidelyke voorstelling. ‘Bien poser une question, c'est presque la résoudre.’ Dit geldt zoowel in menschkunde, moraal, politiek, enz. als in de eigenlyk gezegde wiskunde. De Natuur kent al die onderscheidingen niet. Zy streeft - onbewust - met één middel naar één doel, en er is verband tusschen de helderheid van myn bewys voor de stelling van Pythagoras, en de eenvoudigheid der geloofsbelydenis die ik neerlegde in de vertelling over Lystermannetje.

De leerlingachtige verdeeling in verschillende soort van kundeN

* Volgens 't postulaat, zyn de zyden onderling gelyk, en de hoeken recht. Dat de figuren A B en C D inderdaad vier zyden hebben, en niet meer, wordt hieruit bewezen, dat overäl de tegen die zyden aanliggende hoeken twee rechte uitmaken. (1865)

† De 47e Propositie van Euclides, door J.J.I. Hofmann, hoogleeraar in de wiskunde te Aschaffenburg, vertaald door H. Strootman, lector in de wiskunde, aan de militaire akademie te Breda. (1865)

§ Niemand heeft my de prioriteit betwist. (1872)

[p. 318]

in logiën, is 'n gevolg onzer kleinheid, die niet in-staat is alles te-gelyk te omvatten. Wy ontleden waar de Natuur samenvat, en spellen wat zij schryft. (491) Nu, schande is 't niet, dat wy door spellen tot lezen moeten komen. Maar 't is van belang, te onthouden dat ons spellen geen lezen is.