De Thiende
(1965)–Simon Stevin–
[pagina 19]
| |||||||
1. ‘Bepalinghe’ (Definitions)In I (pp. 10, 11) Stevin points to the fact that Hindu-Arabic numerals denote different values according to their place viz. units, tens, hundreds and so on. So in 1111 each numeral 1 denotes the tenth part of the 1 one place to the left. Stevin's intention is to proceed in this way for fractional parts. To that end he proposes in II (p. 11) for a whole number the name ‘Beghin or ‘Beghinsel’ (commencement), denoted by the sign ⓞ. So the whole number 364 should now be written 364 ⓞ. He then proceeds in III (pp. 11, 12) with the name ‘Eerste’ (prime) for a tenth part of unity, denoted by the sign ①, ‘Tweede’ (second) for a tenth part of an ‘Eerste’, denoted by the sign ② and so on, So the number 8 937/1000 or 8 + 9/10 + 3/100 + 7/1000 should now be written 8 ⓞ 9 ① 3 ② 7 ③. | |||||||
[pagina 20]
| |||||||
These ‘Eerste’, ‘Tweede’ and so on, are called (IIII, p. 12) ‘Thiendetalen’ (dime numbers). As to the origin of this notation G. Sarton (p. 175) makes the following supposition: 8 + 9/10 + 3/100 + 7/1000 can be written with successive powers of 1/10 as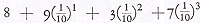 . Consequently the symbols of Stevin are the exponents of powers of 1/10, ② stands for (1/10)2. This supposition is even more probable because Stevin elsewhere uses, in L' Arithmetique, the same symbols - evidently following the Italian mathematician R. Bombelli, 1572 - to denote powers of the unknown in a polynomial, so e.g. 7 ③ + 3 ② - 9 ① means . Consequently the symbols of Stevin are the exponents of powers of 1/10, ② stands for (1/10)2. This supposition is even more probable because Stevin elsewhere uses, in L' Arithmetique, the same symbols - evidently following the Italian mathematician R. Bombelli, 1572 - to denote powers of the unknown in a polynomial, so e.g. 7 ③ + 3 ② - 9 ① means  . .
We, at this time, being familiar with our decimal notation, may consider Stevin's method a clumsy one. But it has been his merit to introduce decimals and to be the first to show clearly their advantages for arithmetic. Before 1585, however, some other decimal notations occurGa naar eind18) of which we will mention here as the best-known example a notation used by Christoff Rudolff in Exempel Buchlin, Augsburg 1530. When calculating compound interest at a rate of 5 per cent., starting with 375 florins, Rudolff writes the amounts for the successive years 393/75, 413/4375, 434/109375 and so | |||||||
[pagina 21]
| |||||||
onGa naar eind19). This notation, indeed, is much more convenient then Stevin's but Rudolff has not a single remark on its advantages nor a treatment of the arithmetical operations. In connection with this it is worth quoting G. Sarton (p. 162): The Thiende was the earliest treatise deliberately devoted to the study of decimal fractions, and Stevin's account was the earliest systematic account of them. Hence, even if decimal fractions were used previously by other men, it was Stevin - and no other - who introduced them into the mathematical domain. That important extension of the idea of number - the creation of the decimal number - was undoubtedly a fruit of his genius, and its occurrence can thus be very exactly dated, - 1585. It would lead us too far to digress upon the development of the decimal notation after Simon Stevin's De Thiende. The interested reader may be referred to the very elaborate survey on this subject by G. Sarton and also to Fl. Cajori, N.L.W.A. Gravelaar, D.E. Smith, D.J. Struik and J. Tropfke. The point as separatrix for the whole and fractional part and also the comma find their origin in the works of the inventor of logarithms John NapierGa naar eind20). But many other notations have been | |||||||
[pagina 22]
| |||||||
suggested and about some of them (not all) is writtenGa naar eind21): For distinguishing of the Decimal Fraction from Integers, it may truly be said, Quot Homines, tot Sententiae; every one fancying severally. For some call the Tenth Parts, the Primes; the Hundredth Parts, Seconds; the Thousandth Parts, Thirds, etc. and mark them with Indices equivalent over their heads. As to express 34 integers and 1426/10000 Parts of a Unit, they do it thus, | |||||||
[pagina 23]
| |||||||
the Cöma is inverted thus, 34'1426, contrary to the true Cöma, and set at top. I sometimes use the one, and sometimes the other, as cometh to hand. It is a well-known fact that even at this time no uniformity exists in the decimal notation for a point as well as a comma are in use as separatrix. Returning to Stevin's notation, we would further remark that upholding his method, some of the signs could be omitted as being superfluous. So 8 937/1000 could also be denoted without any ambiguity as a) 8 ⓞ 937 or b) 8937 ③. | |||||||
2. ‘Werckinghe’ (Operation or practice)The fundamental operations are performed in the same way as with whole numbers, in accordance with what is announced in the title of De Thiende: Leerende door onghehoorde lichticheyt alien rekeningen onder den Menschen noodich vallende, afveerdighen door heele ghetalen sonder ghebrokenen. | |||||||
[pagina 24]
| |||||||
In ‘Vergaderinghe’ (Addition, pp. 13, 14) the numbers have to be written underneath each other with their ‘Eerste’ in one column, the same for their ‘Tweede’ and so on. The method needs no explanation nor does that of ‘Aftreckinghe’ (Subtraction, pp. 14, 15). We only remark that the notation a) mentioned before with the mere sign ⓞ would suffice. In ‘Menigvuldighinghe’ (Multiplication, pp. 16, 17) the ultimate signs of multiplier and multiplicand have to be added. So 378·54 = 20412 and consequently 3 ④ 7 ⑤ 8 ⑥·5 ① 4 ② = 2 ④ 0 ⑤ 4 ⑥ 1 ⑦ 2 ⑧, for 6 + 2 = 8. In ‘Deelinghe’ (Division, pp. 18-20) the ultimate sign of the divisor has to be subtracted from the one of the dividend. If this subtraction is impossible, the dividend has to be supplied with so many zeros as is necessary. So the division 7 ②: 4 ⑤ has to be performed in this way: 7 ② is supplied with zeros to 7 ② 0 ③ 0 ④ 0 ⑤, 7000 : 4 = 1750, 5 - 5 = 0 and consequently 7 ② : 4 ⑤ = 1750. For a non-ending division as 4 ① : 3 ② Stevin remarks (pp. 19, 20): Alwaer blijct datter ... ende dierghelijcke, verloren laet; ... (Whereby appears that there will infinitely come 3's, and in such a case you may come so near as the thing | |||||||
[pagina 25]
| |||||||
requires, omitting the remainder. It is true, that 13 ⓞ 3 ① 3 1/3 ②, or 13 ⓞ 3 ① 3 ② 3 1/3 ③ etc. shall be the perfect quotient required. But our invention in this Dime is to work all by whole numbers. For seeing that in any affairs men reckon not of the thousandth part of a mite, es, grain, etc....)When extracting a square root (pp. 20, 21), the ultimate sign has to be halved, so 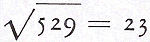 and consequently and consequently  = 2 ① 3 ②. If the ultimate sign is odd, the number has to be supplied with a zero.
This method is very similar to the one used as early as ca. 1343 by John de Meurs of Lisieux, who hasGa naar eind22) = 2 ① 3 ②. If the ultimate sign is odd, the number has to be supplied with a zero.
This method is very similar to the one used as early as ca. 1343 by John de Meurs of Lisieux, who hasGa naar eind22)  As to multiplication, division and the extraction of roots we remark that in these operations the notation b) mentioned before, with only the ultimate sign, would sufficeGa naar eind23). As to multiplication, division and the extraction of roots we remark that in these operations the notation b) mentioned before, with only the ultimate sign, would sufficeGa naar eind23).
| |||||||
3. ‘Aenhangsel’ (Appendix)In the third part of De Thiende Stevin points to the advantages of his decimals for practical computations. To this end a decimal subdivision of the basic-units of money, weights and measures is necessary. | |||||||
[pagina 26]
| |||||||
| |||||||
[pagina 27]
| |||||||
In this last section Stevin again suggests his idea always to stick to the customary basic-units, to call these ‘Beghin’ with the sign ⓞ and to introduce a decimal subdivision. Worth mentioning is the fact that in the case of the ‘Marck’ (mark, a weight-unit) he tries to | |||||||
[pagina 28]
| |||||||
get connection with the existing subdivision by putting 1 ④ of a ‘Marck’ as nearly equal to half an ‘Aes’. In fact a ‘Marck’ is equal to 8 ‘Oncen’ or 8•20 ‘Enghelschen’ or 8•20•32 ‘Azen’ and consequently 1 ④ of a ‘Marck’ is equal to 0.512 of an ‘Aes’. The same is done in the case of a ‘Pondtgroote’ (livre de gros in Flandres; this is a pound, a monetary-unit). The existing subdivisions are: a ‘Pondtgroote’ is equal to 20 ‘Schellingen’ (shillings) or 20•12 ‘Deniers’ or ‘Penninghen’ (denarii, denoted by the symbol 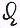 , so ¼ ‘denier’ is slightly more than 1 ③ of a pound. , so ¼ ‘denier’ is slightly more than 1 ③ of a pound.
Stevin seems to have been aware that the proposals made in the ‘Aenhangsel’ would not be realized very soon. On pp. 34, 35 he states: Ten laetsten moeten wy noch ... die mochte ghebruycken. | |||||||
[pagina 29]
| |||||||
happen to every man, to whom it were necessary that the solution so found were of each accepted for good and lawful. Therefore, considering the so great use, it would be a commendable thing, if some of those who expect the greatest commodity would solicit to put the same in execution to effect, namely that joining the vulgar partitions that are now in weight, measures and moneys (continuing still each capital measure, weight and coin in all places unaltered) that the same tenth progression might be lawfully ordained by the superiors for everyone that would use the same). As we know now it has lasted till the beginning of the nineteenth century before a decimal standardization of money, measures and weights has been accepted in most countries. |
|


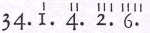 Or thus,
Or thus,  Others thus,
Others thus,  ; or thus,
; or thus,  . And some thus, 34.1.4.2.6. setting the Decimal Parts at little more than ordinary distance one from the other. Others distinguish the Integers from the Decimal Parts only by placing a Cöma before the Decimal Parts thus 34, 1426; a good way and very useful. Others draw a Line under the Decimals thus,
. And some thus, 34.1.4.2.6. setting the Decimal Parts at little more than ordinary distance one from the other. Others distinguish the Integers from the Decimal Parts only by placing a Cöma before the Decimal Parts thus 34, 1426; a good way and very useful. Others draw a Line under the Decimals thus,  , writing them in smaller Figures than the Integers. And others, though they use the work for the best way of distinguishing them, yet after the work is done, they use a Rectangular Line after the place of the Units, called Separatrix, a separating Line, because it separates the Decimal Parts from the Integers, thus
, writing them in smaller Figures than the Integers. And others, though they use the work for the best way of distinguishing them, yet after the work is done, they use a Rectangular Line after the place of the Units, called Separatrix, a separating Line, because it separates the Decimal Parts from the Integers, thus  . And sometimes
. And sometimes